14.1.1 同底数幂的乘法课件(共21张PPT)
文档属性
| 名称 | 14.1.1 同底数幂的乘法课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-02 11:10:27 | ||
图片预览








文档简介
(共21张PPT)
人教版
八年级数学上
14.1.1同底数幂的乘法
学习目标
1.理解并掌握同底数幂的乘法法则.(重点)
2.能够运用同底数幂的乘法法则进行相关计算.(难点)
3.通过对同底数幂的乘法运算法则的推导与总结,提升自身的推理能力.
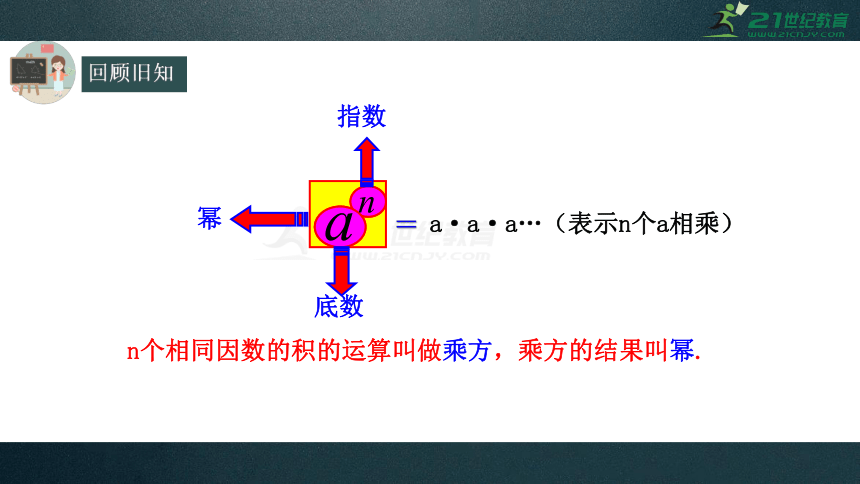
回顾旧知
n个相同因数的积的运算叫做乘方,乘方的结果叫幂.
幂
指数
底数
=
a·a·a…(表示n个a相乘)
情境导入
神威·太湖之光超级计算机是由国家并行计算机工程技术研究中心研制的超级计算机.北京时间2016年6月20日,在法兰克福世界超算大会(ISC)上,“神威·太湖之光”超级计算机系统登顶榜单之首,成为世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
合作探究
神威·太湖之光超级计算机是世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
问题1
怎样列式?
1017
×103
合作探究
问题2
观察算式1017
×103,两个因式有何特点?
观察可以发现,1017
和103这两个因数底数相同,是同底数的幂的形式.
我们把形如1017
×103这种运算叫作同底数幂的乘法.
合作探究
1017×103
=(10×10×10
×…×10)
17个10
×(10×10×10)
3个10
=10×10×…×10
20个10
=1020
=1017+3
(乘方的意义)
(乘法的结合律)
(乘方的意义)
问题3
怎样求解?
合作探究
试一试:根据乘方的意义填空.
(1)25×22=(2×2×2×2×2)
×
(
2×2
)
=2×2×2×2×2
×2×2
=27
(2)a3×a2=(a×a×a)
×(
a×a
)=
a×a×a×a×a
=a5
(3)5m×5n=(5×5×…×5)
×
(5×5×…×5)
=
(5×5×…×5)
=5m+n
(m,n是正整数)
猜一猜:
am
·
an
=a(
)
m+n
合作探究
am·an
=(a·a·…a)
(
个a)
(a·a·…a)
(
个a)
=(a·a·…a)
(
_
个a)
=a(
)
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+
n
m+n
证一证
·
合作探究
am
·
an
=
am+n
(m、n都是正整数).
同底数幂相乘,
底数 ,指数
.
不变
相加.
同底数幂的乘法法则:
知识点拨:、
结果:①底数不变
②指数相加
条件:①乘法
②底数相同
小试牛刀
1.判断下列计算是否正确,并简要说明理由
√
×
×
×
×
am·
an·
ap
=
am+n+p
(m、n、p都是正整数)
想一想:
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示
等于什么呢?
am
·
an
·
ap
x=x1
典例精析
例1
计算:
(1)x2
·
x5
;
(2)a
·
a6;
(3)(-2)
×
(-2)4
×
(-2)3;
(4)
xm
·
x3m+1.
解:(1)
x2
·
x5=
x2+5
=x7
(2)a
·
a6=
a1+6
=
a7;
(3)(-2)
×
(-2)4
×
(-2)3=
(-2)
1+4+3
=
(-2)8
=
256;
(4)
xm
·
x3m+1=
xm+3m+1
=
x4m+1.
学以致用
1、计算:
(1)(a+b)5
·
(a+b)6
;
(2)(m-n)2
·(m-n)5
·(m-n)7
;
(3)(x-y)3·(y-x)5.
解:(1)
(a+b)5
·
(a+b)6
=
(a+b)5+6
=(a+b)11;
(2)(m-n)2
·(m-n)5
·(m-n)7
=(m-n)2+5+7=(m-n)14;
(3)(x-y)3·(y-x)5=(y-x)3(y-x)5
=(y-x)3+5=(y-x)8.
方法总结:公式am
·
an
=
am+n中的底数a还可以代表单项式,多项式.当底数互为相反数的幂相乘时,先把底数统一。
合作探究
2、算一算:
(1)若xa=3,xb=4,xc=5,求2xa+b+c的值.
(2)已知23x+2=32,求x的值;
(2)
∵
23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1)
2xa+b+c=2xa·xb·xc=120.
知识点拨:(1)
am+n=am·
an
am·
an
=
am+n
逆用
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
课堂小结
今天我们收获了哪些知识?
1.说一说同底数幂的乘法法则?法则适用于三个及三个以上的同底数幂相乘吗?
2.同底数幂的乘法法则可以逆用吗?
综合演练
1.下列各式的结果等于28的是(
)
A
2+25
B
2·25
C
23·25
D
0.22·
0.24
C
2.下列计算结果正确的是(
)
A
a3
·
a3=a9
B
m2
·
n2=mn4
C
xm
·
x3=x3m
D
y
·
yn=yn+1
D
综合演练
3、在等式a·a4·_____=a8中,横线上所填的代数式应当是
(
)
A.a3
B.a4
C.a5
D.a6
4、已知am=3,am+n=18,求an的值是____.
A
6
综合演练
(1)x·x2·x(
)=x9;
(2)xm·(
)=x5m;
(3)16×4=2x,则x=(
).
6
6
x4m
6.填空:
5.计算:
(1)
xn+1·x3n=_______;
(2)
(a-b)3·(a-b)3=_______;
(3)
-a6·(-a)2=_______;
(4)
y4·y3·y2·y
=_______.
x4n+1
(a-b)6
-a8
y10
综合演练
6.计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)5·(b-a)4;
(3)
(-3)×(-3)3
×(-3)3;
(1)(2a+b)2n+1·(2a+b)4;
解:(1)(2a+b)2n+1·(2a+b)4=(2a+b)2n+5;
(2)(a-b)5·(b-a)4=(a-b)9;
(3)
(-3)×(-3)3
×(-3)3=-37;
(4)-a3·(-a)4·(-a)3=a10.
课后作业
教材96页练习题(1)-(4)题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
14.1.1同底数幂的乘法
学习目标
1.理解并掌握同底数幂的乘法法则.(重点)
2.能够运用同底数幂的乘法法则进行相关计算.(难点)
3.通过对同底数幂的乘法运算法则的推导与总结,提升自身的推理能力.
回顾旧知
n个相同因数的积的运算叫做乘方,乘方的结果叫幂.
幂
指数
底数
=
a·a·a…(表示n个a相乘)
情境导入
神威·太湖之光超级计算机是由国家并行计算机工程技术研究中心研制的超级计算机.北京时间2016年6月20日,在法兰克福世界超算大会(ISC)上,“神威·太湖之光”超级计算机系统登顶榜单之首,成为世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
合作探究
神威·太湖之光超级计算机是世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
问题1
怎样列式?
1017
×103
合作探究
问题2
观察算式1017
×103,两个因式有何特点?
观察可以发现,1017
和103这两个因数底数相同,是同底数的幂的形式.
我们把形如1017
×103这种运算叫作同底数幂的乘法.
合作探究
1017×103
=(10×10×10
×…×10)
17个10
×(10×10×10)
3个10
=10×10×…×10
20个10
=1020
=1017+3
(乘方的意义)
(乘法的结合律)
(乘方的意义)
问题3
怎样求解?
合作探究
试一试:根据乘方的意义填空.
(1)25×22=(2×2×2×2×2)
×
(
2×2
)
=2×2×2×2×2
×2×2
=27
(2)a3×a2=(a×a×a)
×(
a×a
)=
a×a×a×a×a
=a5
(3)5m×5n=(5×5×…×5)
×
(5×5×…×5)
=
(5×5×…×5)
=5m+n
(m,n是正整数)
猜一猜:
am
·
an
=a(
)
m+n
合作探究
am·an
=(a·a·…a)
(
个a)
(a·a·…a)
(
个a)
=(a·a·…a)
(
_
个a)
=a(
)
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+
n
m+n
证一证
·
合作探究
am
·
an
=
am+n
(m、n都是正整数).
同底数幂相乘,
底数 ,指数
.
不变
相加.
同底数幂的乘法法则:
知识点拨:、
结果:①底数不变
②指数相加
条件:①乘法
②底数相同
小试牛刀
1.判断下列计算是否正确,并简要说明理由
√
×
×
×
×
am·
an·
ap
=
am+n+p
(m、n、p都是正整数)
想一想:
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示
等于什么呢?
am
·
an
·
ap
x=x1
典例精析
例1
计算:
(1)x2
·
x5
;
(2)a
·
a6;
(3)(-2)
×
(-2)4
×
(-2)3;
(4)
xm
·
x3m+1.
解:(1)
x2
·
x5=
x2+5
=x7
(2)a
·
a6=
a1+6
=
a7;
(3)(-2)
×
(-2)4
×
(-2)3=
(-2)
1+4+3
=
(-2)8
=
256;
(4)
xm
·
x3m+1=
xm+3m+1
=
x4m+1.
学以致用
1、计算:
(1)(a+b)5
·
(a+b)6
;
(2)(m-n)2
·(m-n)5
·(m-n)7
;
(3)(x-y)3·(y-x)5.
解:(1)
(a+b)5
·
(a+b)6
=
(a+b)5+6
=(a+b)11;
(2)(m-n)2
·(m-n)5
·(m-n)7
=(m-n)2+5+7=(m-n)14;
(3)(x-y)3·(y-x)5=(y-x)3(y-x)5
=(y-x)3+5=(y-x)8.
方法总结:公式am
·
an
=
am+n中的底数a还可以代表单项式,多项式.当底数互为相反数的幂相乘时,先把底数统一。
合作探究
2、算一算:
(1)若xa=3,xb=4,xc=5,求2xa+b+c的值.
(2)已知23x+2=32,求x的值;
(2)
∵
23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1)
2xa+b+c=2xa·xb·xc=120.
知识点拨:(1)
am+n=am·
an
am·
an
=
am+n
逆用
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
课堂小结
今天我们收获了哪些知识?
1.说一说同底数幂的乘法法则?法则适用于三个及三个以上的同底数幂相乘吗?
2.同底数幂的乘法法则可以逆用吗?
综合演练
1.下列各式的结果等于28的是(
)
A
2+25
B
2·25
C
23·25
D
0.22·
0.24
C
2.下列计算结果正确的是(
)
A
a3
·
a3=a9
B
m2
·
n2=mn4
C
xm
·
x3=x3m
D
y
·
yn=yn+1
D
综合演练
3、在等式a·a4·_____=a8中,横线上所填的代数式应当是
(
)
A.a3
B.a4
C.a5
D.a6
4、已知am=3,am+n=18,求an的值是____.
A
6
综合演练
(1)x·x2·x(
)=x9;
(2)xm·(
)=x5m;
(3)16×4=2x,则x=(
).
6
6
x4m
6.填空:
5.计算:
(1)
xn+1·x3n=_______;
(2)
(a-b)3·(a-b)3=_______;
(3)
-a6·(-a)2=_______;
(4)
y4·y3·y2·y
=_______.
x4n+1
(a-b)6
-a8
y10
综合演练
6.计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)5·(b-a)4;
(3)
(-3)×(-3)3
×(-3)3;
(1)(2a+b)2n+1·(2a+b)4;
解:(1)(2a+b)2n+1·(2a+b)4=(2a+b)2n+5;
(2)(a-b)5·(b-a)4=(a-b)9;
(3)
(-3)×(-3)3
×(-3)3=-37;
(4)-a3·(-a)4·(-a)3=a10.
课后作业
教材96页练习题(1)-(4)题.
https://www.21cnjy.com/help/help_extract.php
