山东省东营市垦利区2019—2020学年度第一学期期末考试六年级数学试卷(Word版,附答案)
文档属性
| 名称 | 山东省东营市垦利区2019—2020学年度第一学期期末考试六年级数学试卷(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 137.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-01 23:04:33 | ||
图片预览


文档简介
东营市垦利区2019?—2020学年度第一学期期末考试
六年级数学试题
(考试时间:120分钟
分值:120分)
注意事项:
1.数学试题共4页.答题前,考生务必将自己的姓名、班级、学校、准考证号等填写在答题卡上.
2.第一大题每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.第二、三大题按要求用0.5mm碳素笔答在答题卡的相应位置上.
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,不选或选出的答案超过一个均记零分。)
第I卷(选择题
共30分)
1.比﹣4小的数是( )
A.﹣2
B.﹣1
C.﹣6
D.6
2.
下列计算正确的是( )
A.3a+4b=7ab
B.x6+x6=x12
C.﹣2(a+b)=﹣2a+2b
D.2x2+3x2=5x2
3.下列四个立体图形中,从正面看到的图形与其他三个不同的是( )
A.
B.
C.
D.
4.下列各组数中,相等的是( )
A.﹣1与(﹣2)+(﹣3)
B.|﹣5|与﹣(﹣5)
C.与
D.(﹣2)2与﹣4
5.若x=1是关于x的方程2x-a=0的解,则a的值是( )
A.-2
B.1
C.-1
D.2
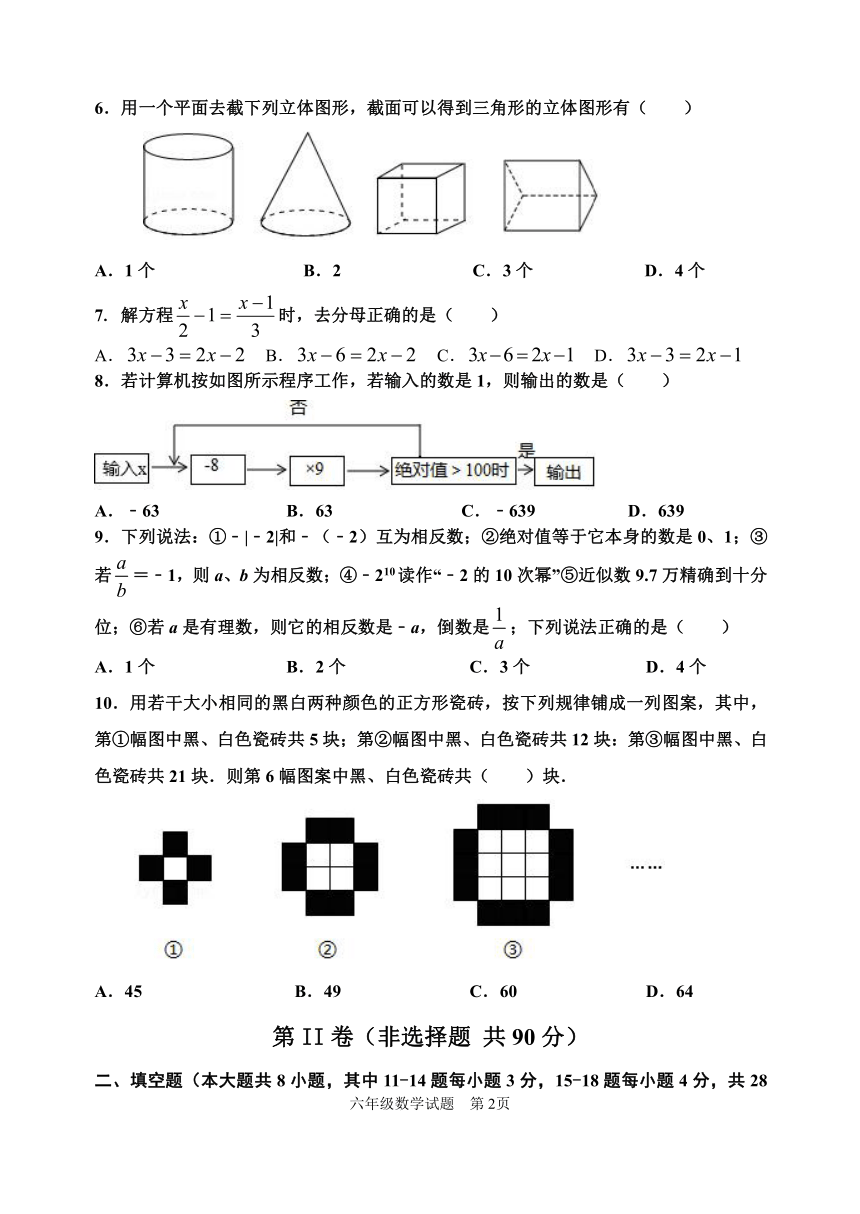
6.用一个平面去截下列立体图形,截面可以得到三角形的立体图形有( )
A.1个
B.2
C.3个
D.4个
7.
解方程时,去分母正确的是( )
A. B. C. D.
8.若计算机按如图所示程序工作,若输入的数是1,则输出的数是( )
A.﹣63
B.63
C.﹣639
D.639
9.下列说法:①﹣|﹣2|和﹣(﹣2)互为相反数;②绝对值等于它本身的数是0、1;③若=﹣1,则a、b为相反数;④﹣210读作“﹣2的10次幂”⑤近似数9.7万精确到十分位;⑥若a是有理数,则它的相反数是﹣a,倒数是;下列说法正确的是( )
A.1个
B.2个
C.3个
D.4个
10.用若干大小相同的黑白两种颜色的正方形瓷砖,按下列规律铺成一列图案,其中,第①幅图中黑、白色瓷砖共5块;第②幅图中黑、白色瓷砖共12块:第③幅图中黑、白色瓷砖共21块.则第6幅图案中黑、白色瓷砖共( )块.
A.45
B.49
C.60
D.64
第II卷(非选择题
共90分)
二、填空题(本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.)
11.根据教育部的消息,2019年参加高考的考生人数为1031万人,1031万用科学记数法表示为__________.
12.单项式5mn2的次数是__________.
13.如图所示的是一个正方体的展开图,它的每一个面上都
写有一个自然数,并且相对的两个面的两个数字相等,那么
a+b﹣2c=__________.
14.若是一元一次方程,那么__________.
15.若x+y=3,xy=2.则(4x+2)﹣(3xy﹣4y)=__________.
16.如果多项式﹣8x2+x﹣1与关于x的多项式2mx2+3x﹣7的和不含二次项,则m=__________.
17.某种商品每件的标价为240元,按标价的八折销售时,每件仍能获利20%,则这种商品每件的进价为_______元
18.一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折2次后,可以得3条折痕,那么对折5次可以得到
条折痕.
三、解答题(本大题共7小题,满分62分,解答应写出必要的文字说明、证明过程或推演步骤)
19.计算(本题满分7分,第(1)题3分,第(2)题4分)
(1)(﹣)÷(﹣2)2×|﹣12|
(2)(﹣5)3×(﹣)﹣32÷(﹣2)2×(+)
20.
解方程(本题满分8分,
每小题4分)
(1)12(2-3x)=4x+4
(2)
21.(本题满分8分)
已知下列有理数:﹣(﹣3)、﹣4、0、+5、﹣
(1)这些有理数中,整数有
个,非负数有
个.
(2)画数轴,并在数轴上表示这些有理数.
(3)把这些有理数用“<“号连接起来:
_______________.
22.(本题满分8分)
周末小彬和小明相约骑自行车去图书馆,事先决定早晨7:00从家里出发,预计每小时行7.5km,上午9:00可到达目的地.出发前他们又决定上午8:30到达目的地,那么每小时要行多少千米?
23.(本题满分9分)
已知:A=2x2+3xy+2y﹣1,B=x2﹣xy.
(1)计算:A﹣2B;
(2)若(x+1)2+|y﹣2|=0,求A﹣2B的值;
(3)若A﹣2B的值与y的取值无关,求x的值.
24.(本题满分10分)
结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是______;数轴上表示﹣3和2两点之间的距离是______;
一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如数轴上数x与5两点之间的距离等于|x﹣5|,
(2)如果表示数a和﹣2的两点之间的距离是3,那么a=______;若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
25.(本题满分12分)
我市某学校组织一批学生开展社会实践活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元.
(1)这批学生的人数是多少?原计划租用45座客车多少辆?
(2)若租用同一种客车,要使每位学生都有座位,应该怎样租用才合算?
2019-2020学年度第一学期期末考试
六年级数学试题答案及评分标准
一.选择题:
1.C
2.
D
3.A
4.B
5.D
6.
B
7.
B
8.
C
9.B
10.C
二.填空题:
11.
1.031×107
12.
3 13.
-38
14.
1
15.
8
16.
4
17.
160
18.
31
三、解答题:
19.解:(1)原式=﹣××12=﹣2;┄┈┄┄┄3分
(2)原式=﹣125×(﹣)﹣32××=75﹣10=65.┄┈┄┄┄7分
20.解:(1)去括号得24-36x=4x+4
┄┈┄┄┄1分
移项、合并同类项得-40x=-20
┄┈┄┄┄3分
系数化1得x=
┄┈┄┄┄4分
(2)去分母得3(x-3)-2(2x+1)=6
┄┈┄┄┄5分
去括号得3x-9-4x-2=6
┄┈┄┄┄6分
移项、合并同类项得-x=17
┄┈┄┄┄7分
系数化1得x=
-17
┄┈┄┄┄8分
21.
解:(1)这些有理数中,整数有:﹣(﹣3)、﹣4、0、+5,共4个,┄┈┄2分
非负数有:﹣(﹣3)、0、+5,共3个.┄┈┄┄┄4分
(2)在数轴上表示这些有理数如图:
┄┈┄┄┄6分
(3)根据数轴可得:﹣4<﹣<0<﹣(﹣3)<+5.┄┈┄┄┄8分
22.解:设每小时行驶x千米,由题意列
x×1.5x=7.5×2
┄┈┄┄┄5分
解得x=10
┄┈┄┄┄7分
答:每小时行驶10千米
┄┈┄┄┄8分
23.
解:(1)∵A=2x2+3xy+2y﹣1,B=x2﹣xy,
∴A﹣2B=2x2+3xy+2y﹣1﹣2x2+2xy=5xy+2y﹣1;┄┈┄┄┄3分
(2)∵(x+1)2+|y﹣2|=0,
∴x=﹣1,y=2,
则A﹣2B=﹣10+4﹣1=﹣7;┄┈┄┄┄6分
(3)A﹣2B=5xy+2y﹣1=(5x+2)y﹣1,
由结果与y的取值无关,得到5x+2=0,
解得:x=﹣.┄┈┄┄┄9分声明:试题
24.解:(1)观察数轴可得:数轴上表示4和1的两点之间的距离是3;数轴上表示﹣3和2两点之间的距离是5;
故答案为:3;5;┄┈┄┄┄2分
(2)如果表示数a和﹣2的两点之间的距离是3,那么|a﹣(﹣2)|=3
∴|a+2|=3
∴a+2=3或a+2=﹣3
∴a=1或a=﹣5;
故答案为:1或﹣5;┄┈┄┄┄4分
∵|a+4|+|a﹣2|表示数a与﹣4的距离与a和2的距离之和;
若数轴上表示数a的点位于﹣4与2之间,则|a+4|+|a﹣2|的值等于2和﹣4之间的距离,等于6
∴|a+4|+|a﹣2|的值为6;┄┈┄┄┄7分
(3)|a+5|+|a﹣1|+|a﹣4|表示一点到﹣5,1,4三点的距离的和
∴当a=1时,该式的值最小,最小值为6+0+3=9.┄┈┄┄┄10分
25.解:设原计划租用45座客车x辆,则这批学生的人数为(45x+15)┄┈┄┄┄1分
由题意得60(x-1)=45x+15
┄┈┄┄┄4分
解得x=5
┄┈┄┄┄5分
45x+15=240
┄┈┄┄┄6分
即:这批学生人数为240人,原计划租用45座客车5辆.
┄┈┄┄┄7分
(2)由题意得:租45座客车6辆,租60座客车4辆┄┈┄┄┄9分
租45座客车费用:220×6=1320(元);租69座客车费用:300×4=1200(元)┄┄11分∵1320>1200
∴租用同一种客车,要使每位学生都有座位,租用4辆60座客车更合算┄┈┄┄12分
六年级数学试题
第1页
六年级数学试题
(考试时间:120分钟
分值:120分)
注意事项:
1.数学试题共4页.答题前,考生务必将自己的姓名、班级、学校、准考证号等填写在答题卡上.
2.第一大题每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.第二、三大题按要求用0.5mm碳素笔答在答题卡的相应位置上.
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,不选或选出的答案超过一个均记零分。)
第I卷(选择题
共30分)
1.比﹣4小的数是( )
A.﹣2
B.﹣1
C.﹣6
D.6
2.
下列计算正确的是( )
A.3a+4b=7ab
B.x6+x6=x12
C.﹣2(a+b)=﹣2a+2b
D.2x2+3x2=5x2
3.下列四个立体图形中,从正面看到的图形与其他三个不同的是( )
A.
B.
C.
D.
4.下列各组数中,相等的是( )
A.﹣1与(﹣2)+(﹣3)
B.|﹣5|与﹣(﹣5)
C.与
D.(﹣2)2与﹣4
5.若x=1是关于x的方程2x-a=0的解,则a的值是( )
A.-2
B.1
C.-1
D.2
6.用一个平面去截下列立体图形,截面可以得到三角形的立体图形有( )
A.1个
B.2
C.3个
D.4个
7.
解方程时,去分母正确的是( )
A. B. C. D.
8.若计算机按如图所示程序工作,若输入的数是1,则输出的数是( )
A.﹣63
B.63
C.﹣639
D.639
9.下列说法:①﹣|﹣2|和﹣(﹣2)互为相反数;②绝对值等于它本身的数是0、1;③若=﹣1,则a、b为相反数;④﹣210读作“﹣2的10次幂”⑤近似数9.7万精确到十分位;⑥若a是有理数,则它的相反数是﹣a,倒数是;下列说法正确的是( )
A.1个
B.2个
C.3个
D.4个
10.用若干大小相同的黑白两种颜色的正方形瓷砖,按下列规律铺成一列图案,其中,第①幅图中黑、白色瓷砖共5块;第②幅图中黑、白色瓷砖共12块:第③幅图中黑、白色瓷砖共21块.则第6幅图案中黑、白色瓷砖共( )块.
A.45
B.49
C.60
D.64
第II卷(非选择题
共90分)
二、填空题(本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.)
11.根据教育部的消息,2019年参加高考的考生人数为1031万人,1031万用科学记数法表示为__________.
12.单项式5mn2的次数是__________.
13.如图所示的是一个正方体的展开图,它的每一个面上都
写有一个自然数,并且相对的两个面的两个数字相等,那么
a+b﹣2c=__________.
14.若是一元一次方程,那么__________.
15.若x+y=3,xy=2.则(4x+2)﹣(3xy﹣4y)=__________.
16.如果多项式﹣8x2+x﹣1与关于x的多项式2mx2+3x﹣7的和不含二次项,则m=__________.
17.某种商品每件的标价为240元,按标价的八折销售时,每件仍能获利20%,则这种商品每件的进价为_______元
18.一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折2次后,可以得3条折痕,那么对折5次可以得到
条折痕.
三、解答题(本大题共7小题,满分62分,解答应写出必要的文字说明、证明过程或推演步骤)
19.计算(本题满分7分,第(1)题3分,第(2)题4分)
(1)(﹣)÷(﹣2)2×|﹣12|
(2)(﹣5)3×(﹣)﹣32÷(﹣2)2×(+)
20.
解方程(本题满分8分,
每小题4分)
(1)12(2-3x)=4x+4
(2)
21.(本题满分8分)
已知下列有理数:﹣(﹣3)、﹣4、0、+5、﹣
(1)这些有理数中,整数有
个,非负数有
个.
(2)画数轴,并在数轴上表示这些有理数.
(3)把这些有理数用“<“号连接起来:
_______________.
22.(本题满分8分)
周末小彬和小明相约骑自行车去图书馆,事先决定早晨7:00从家里出发,预计每小时行7.5km,上午9:00可到达目的地.出发前他们又决定上午8:30到达目的地,那么每小时要行多少千米?
23.(本题满分9分)
已知:A=2x2+3xy+2y﹣1,B=x2﹣xy.
(1)计算:A﹣2B;
(2)若(x+1)2+|y﹣2|=0,求A﹣2B的值;
(3)若A﹣2B的值与y的取值无关,求x的值.
24.(本题满分10分)
结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是______;数轴上表示﹣3和2两点之间的距离是______;
一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如数轴上数x与5两点之间的距离等于|x﹣5|,
(2)如果表示数a和﹣2的两点之间的距离是3,那么a=______;若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
25.(本题满分12分)
我市某学校组织一批学生开展社会实践活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元.
(1)这批学生的人数是多少?原计划租用45座客车多少辆?
(2)若租用同一种客车,要使每位学生都有座位,应该怎样租用才合算?
2019-2020学年度第一学期期末考试
六年级数学试题答案及评分标准
一.选择题:
1.C
2.
D
3.A
4.B
5.D
6.
B
7.
B
8.
C
9.B
10.C
二.填空题:
11.
1.031×107
12.
3 13.
-38
14.
1
15.
8
16.
4
17.
160
18.
31
三、解答题:
19.解:(1)原式=﹣××12=﹣2;┄┈┄┄┄3分
(2)原式=﹣125×(﹣)﹣32××=75﹣10=65.┄┈┄┄┄7分
20.解:(1)去括号得24-36x=4x+4
┄┈┄┄┄1分
移项、合并同类项得-40x=-20
┄┈┄┄┄3分
系数化1得x=
┄┈┄┄┄4分
(2)去分母得3(x-3)-2(2x+1)=6
┄┈┄┄┄5分
去括号得3x-9-4x-2=6
┄┈┄┄┄6分
移项、合并同类项得-x=17
┄┈┄┄┄7分
系数化1得x=
-17
┄┈┄┄┄8分
21.
解:(1)这些有理数中,整数有:﹣(﹣3)、﹣4、0、+5,共4个,┄┈┄2分
非负数有:﹣(﹣3)、0、+5,共3个.┄┈┄┄┄4分
(2)在数轴上表示这些有理数如图:
┄┈┄┄┄6分
(3)根据数轴可得:﹣4<﹣<0<﹣(﹣3)<+5.┄┈┄┄┄8分
22.解:设每小时行驶x千米,由题意列
x×1.5x=7.5×2
┄┈┄┄┄5分
解得x=10
┄┈┄┄┄7分
答:每小时行驶10千米
┄┈┄┄┄8分
23.
解:(1)∵A=2x2+3xy+2y﹣1,B=x2﹣xy,
∴A﹣2B=2x2+3xy+2y﹣1﹣2x2+2xy=5xy+2y﹣1;┄┈┄┄┄3分
(2)∵(x+1)2+|y﹣2|=0,
∴x=﹣1,y=2,
则A﹣2B=﹣10+4﹣1=﹣7;┄┈┄┄┄6分
(3)A﹣2B=5xy+2y﹣1=(5x+2)y﹣1,
由结果与y的取值无关,得到5x+2=0,
解得:x=﹣.┄┈┄┄┄9分声明:试题
24.解:(1)观察数轴可得:数轴上表示4和1的两点之间的距离是3;数轴上表示﹣3和2两点之间的距离是5;
故答案为:3;5;┄┈┄┄┄2分
(2)如果表示数a和﹣2的两点之间的距离是3,那么|a﹣(﹣2)|=3
∴|a+2|=3
∴a+2=3或a+2=﹣3
∴a=1或a=﹣5;
故答案为:1或﹣5;┄┈┄┄┄4分
∵|a+4|+|a﹣2|表示数a与﹣4的距离与a和2的距离之和;
若数轴上表示数a的点位于﹣4与2之间,则|a+4|+|a﹣2|的值等于2和﹣4之间的距离,等于6
∴|a+4|+|a﹣2|的值为6;┄┈┄┄┄7分
(3)|a+5|+|a﹣1|+|a﹣4|表示一点到﹣5,1,4三点的距离的和
∴当a=1时,该式的值最小,最小值为6+0+3=9.┄┈┄┄┄10分
25.解:设原计划租用45座客车x辆,则这批学生的人数为(45x+15)┄┈┄┄┄1分
由题意得60(x-1)=45x+15
┄┈┄┄┄4分
解得x=5
┄┈┄┄┄5分
45x+15=240
┄┈┄┄┄6分
即:这批学生人数为240人,原计划租用45座客车5辆.
┄┈┄┄┄7分
(2)由题意得:租45座客车6辆,租60座客车4辆┄┈┄┄┄9分
租45座客车费用:220×6=1320(元);租69座客车费用:300×4=1200(元)┄┄11分∵1320>1200
∴租用同一种客车,要使每位学生都有座位,租用4辆60座客车更合算┄┈┄┄12分
六年级数学试题
第1页
同课章节目录
