2010学年新人教从化七中九年级上《点和圆的位置关系》导学案
文档属性
| 名称 | 2010学年新人教从化七中九年级上《点和圆的位置关系》导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 24.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-11 13:28:16 | ||
图片预览
文档简介
24.2.1点与圆的位置关系导学案
班级: 主备教师:王国鑫 备课组长: 领导批阅: 上课时间: 年 月 日
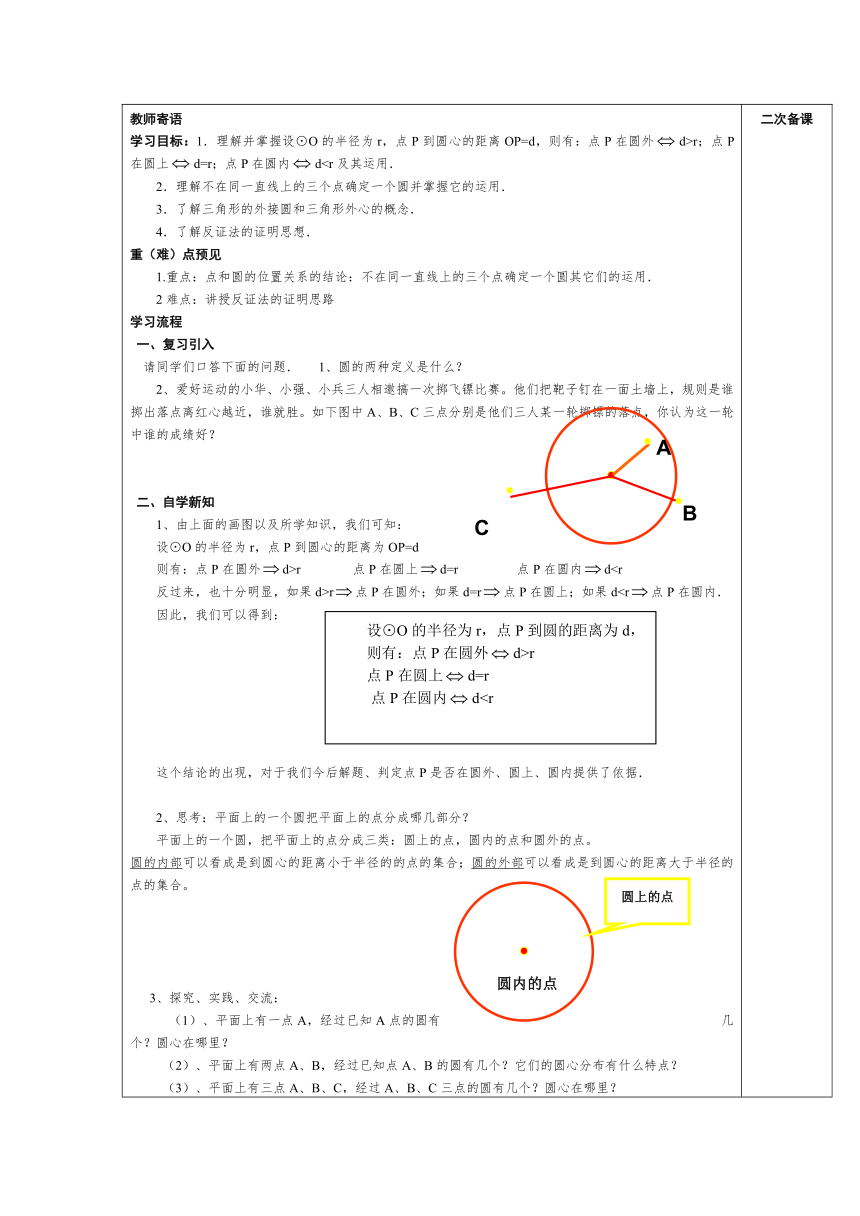
1、由上面的画图以及所学知识,我们可知:
③以O为圆心,以OA为半径作圆,⊙O就是所要求作的圆,如图3所示.
在上面的作图过程中,因为直线DE与FG只有一个交点O,并且点O到A、B、C三个点的距离相等(中垂线上的任一点到两边的距离相等),所以经过A、B、C三点可以作一个圆,并且只能作一个圆.即:不在同一直线上的三个点确定一个圆.将上述结论用于三角形,可得:5、有关概念: 1、 经过三角形的三个顶点可以做一个圆,并且只能画一个圆,这个圆叫做三角形的外接圆. 2、外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心.3、三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。想一想:1、一个三角形的外接圆有几个?一个圆的内接三角形有几个?2、如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.3、任意四个点是不是可以作一个圆?请举例说明.三、自学检测1、已知矩形ABCD的边AB=3厘米,AD=4厘米(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?2、判断下列说法是否正确(1)任意的一个三角形一定有一个外接圆( ).(2)任意一个圆有且只有一个内接三角形( )(3)经过三点一定可以确定一个圆( )(4)三角形的外心到三角形各顶点的距离相等( )四、当堂训练课本93页练习1.2.3.4题五、归纳总结:本节课你有哪些收获?请与同学们分享。教学反思布置作业:P101习题24.2复习巩固1,综合运用8、10(第10题做在书上)第二课时一、复习,引入新课做一做:1、分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.(P102综合运用8) 2、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的的安全区域,已知这个导火索的长度为18cm,如果点导火索的人以每秒6.5m的速度撤离,那么是否安全?为什么?思考:经过同一条直线上的三个点能做出一个圆吗?(幻灯片22)证明:如图,假设过同一直线L上的A、B、C三点可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线L1,又在线段BC的垂直平分线L2,即点P为L1与L2点,而L1⊥L,L2⊥L,这与我们以前所学的“过一点有且只有一条直线与已知直线垂直”矛盾.所以,过同一直线上的三点不能作圆. 上面的证明方法与我们前面所学的证明方法思路不同,它不是直接从命题的已知得出结论,而是假设命题的结论不成立(即假设过同一直线上的三点可以作一个圆),由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到命题成立.这种证明方法叫做反证法.(幻灯片23) 在某些情景下,反证法是很有效的证明方法.例题:用反证法证明:两直线平行,同位角相等。分析:1、题设和结论分别是什么?2、如何假设?3、如何证明?三、巩固练习四、课后反思:用反证法证明“一个三角形中必有一个内角小于或等于60度”,该如何假设?这个问题没有讲解清楚。 教学反思(黑体小五号):内容 小五仿宋-GB2312 不加粗 单倍行距 二次备课
A
C
B
圆内的点
圆上的点
设⊙O的半径为r,点P到圆的距离为d,
则有:点P在圆外d>r
点P在圆上d=r
点P在圆内dA
B
C
D
E
F
1
2
O
班级: 主备教师:王国鑫 备课组长: 领导批阅: 上课时间: 年 月 日
1、由上面的画图以及所学知识,我们可知:
③以O为圆心,以OA为半径作圆,⊙O就是所要求作的圆,如图3所示.
在上面的作图过程中,因为直线DE与FG只有一个交点O,并且点O到A、B、C三个点的距离相等(中垂线上的任一点到两边的距离相等),所以经过A、B、C三点可以作一个圆,并且只能作一个圆.即:不在同一直线上的三个点确定一个圆.将上述结论用于三角形,可得:5、有关概念: 1、 经过三角形的三个顶点可以做一个圆,并且只能画一个圆,这个圆叫做三角形的外接圆. 2、外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心.3、三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。想一想:1、一个三角形的外接圆有几个?一个圆的内接三角形有几个?2、如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.3、任意四个点是不是可以作一个圆?请举例说明.三、自学检测1、已知矩形ABCD的边AB=3厘米,AD=4厘米(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?2、判断下列说法是否正确(1)任意的一个三角形一定有一个外接圆( ).(2)任意一个圆有且只有一个内接三角形( )(3)经过三点一定可以确定一个圆( )(4)三角形的外心到三角形各顶点的距离相等( )四、当堂训练课本93页练习1.2.3.4题五、归纳总结:本节课你有哪些收获?请与同学们分享。教学反思布置作业:P101习题24.2复习巩固1,综合运用8、10(第10题做在书上)第二课时一、复习,引入新课做一做:1、分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.(P102综合运用8) 2、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的的安全区域,已知这个导火索的长度为18cm,如果点导火索的人以每秒6.5m的速度撤离,那么是否安全?为什么?思考:经过同一条直线上的三个点能做出一个圆吗?(幻灯片22)证明:如图,假设过同一直线L上的A、B、C三点可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线L1,又在线段BC的垂直平分线L2,即点P为L1与L2点,而L1⊥L,L2⊥L,这与我们以前所学的“过一点有且只有一条直线与已知直线垂直”矛盾.所以,过同一直线上的三点不能作圆. 上面的证明方法与我们前面所学的证明方法思路不同,它不是直接从命题的已知得出结论,而是假设命题的结论不成立(即假设过同一直线上的三点可以作一个圆),由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到命题成立.这种证明方法叫做反证法.(幻灯片23) 在某些情景下,反证法是很有效的证明方法.例题:用反证法证明:两直线平行,同位角相等。分析:1、题设和结论分别是什么?2、如何假设?3、如何证明?三、巩固练习四、课后反思:用反证法证明“一个三角形中必有一个内角小于或等于60度”,该如何假设?这个问题没有讲解清楚。 教学反思(黑体小五号):内容 小五仿宋-GB2312 不加粗 单倍行距 二次备课
A
C
B
圆内的点
圆上的点
设⊙O的半径为r,点P到圆的距离为d,
则有:点P在圆外d>r
点P在圆上d=r
点P在圆内d
B
C
D
E
F
1
2
O
同课章节目录
