九年级上《公式法》第1课时导学案
图片预览

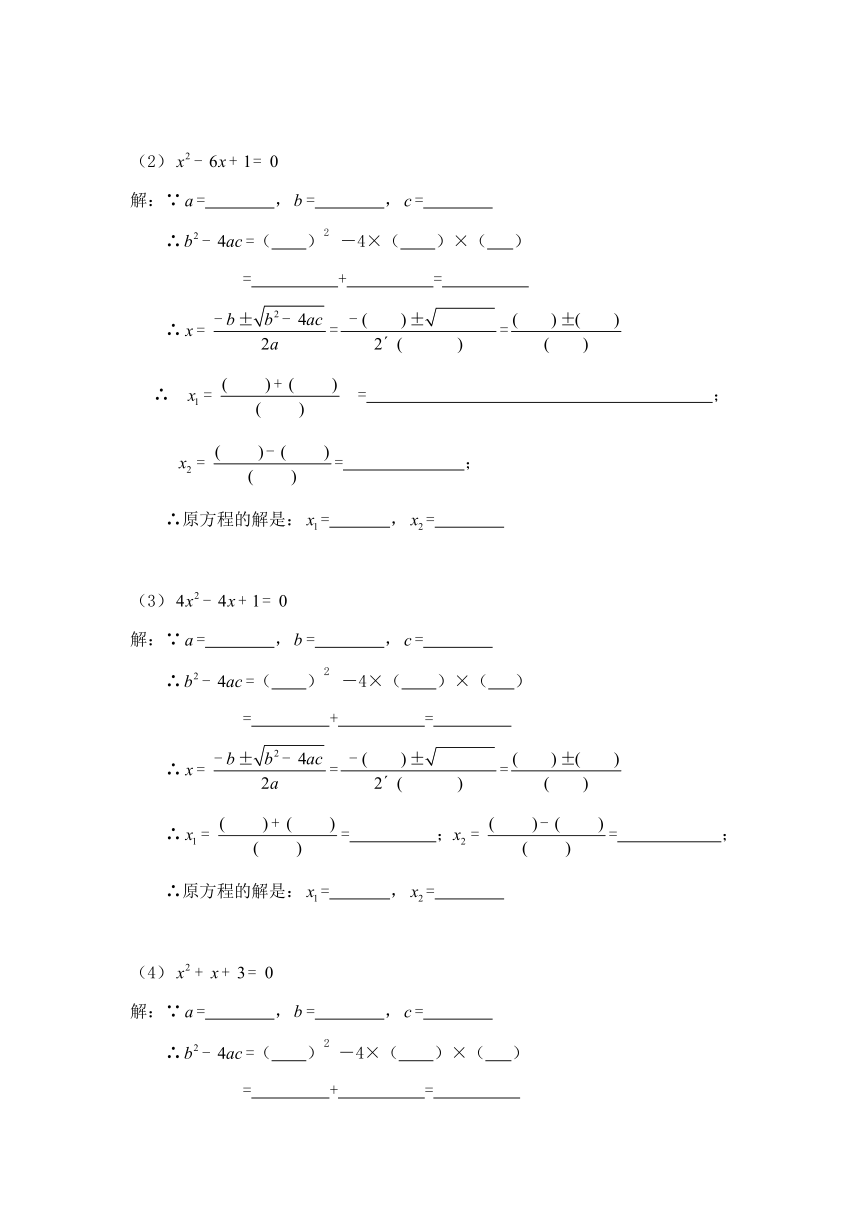
文档简介
(九年级数学)第23章一元二次方程(三)——公式法
第 周 星期 班别_______ 姓名___ _____ 学号_____
一、学习目标:
正确运用求根公式解一元二次方程。
二、学习过程:
环节一:复习回顾
1、一元二次方程的一般形式:
2、运用求根公式解一元二次方程:
一元二次方程()的求根公式:
()
运用此公式注意:必须把方程化为一般形式。
环节二: 练习A:
1、用公式法解方程:
(1)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
∴==
∴= ;= ;
∴原方程的解是:= ,=
(2)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
∴==
∴= ;= ;
∴原方程的解是:= ,=
(3)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
∴==
∴= ;= ;
∴原方程的解是:= ,=
(4)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
思考:此时 0(填“>”、”<”);
因为负数 平方根(横线上填“有”或“没有”),
所以此时 平方根(横线上填“有”或“没有”);
所以原方程 实数解(横线上填“有”或“没有”)。
**小结:
关于一元二次方程的解有三种情况:
当 0时,方程有两个不相等的实数解;
当 0时,方程有两个相等的实数解;
当 0时,方程没有实数解;
(5)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
(6)
解:
B组:
1、解方程:
(1)
解:∵= ,= ,=
(2)
解:将方程化为一般形式,得:
∵= ,= ,=
∴=
(3)
解:将方程化为一般形式,得:
∵= ,= ,=
∴=
第 周 星期 班别_______ 姓名___ _____ 学号_____
一、学习目标:
正确运用求根公式解一元二次方程。
二、学习过程:
环节一:复习回顾
1、一元二次方程的一般形式:
2、运用求根公式解一元二次方程:
一元二次方程()的求根公式:
()
运用此公式注意:必须把方程化为一般形式。
环节二: 练习A:
1、用公式法解方程:
(1)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
∴==
∴= ;= ;
∴原方程的解是:= ,=
(2)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
∴==
∴= ;= ;
∴原方程的解是:= ,=
(3)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
∴==
∴= ;= ;
∴原方程的解是:= ,=
(4)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
思考:此时 0(填“>”、”<”);
因为负数 平方根(横线上填“有”或“没有”),
所以此时 平方根(横线上填“有”或“没有”);
所以原方程 实数解(横线上填“有”或“没有”)。
**小结:
关于一元二次方程的解有三种情况:
当 0时,方程有两个不相等的实数解;
当 0时,方程有两个相等的实数解;
当 0时,方程没有实数解;
(5)
解:∵= ,= ,=
∴=( )2 -4×( )×( )
= + =
(6)
解:
B组:
1、解方程:
(1)
解:∵= ,= ,=
(2)
解:将方程化为一般形式,得:
∵= ,= ,=
∴=
(3)
解:将方程化为一般形式,得:
∵= ,= ,=
∴=
