函数单调性

(共19张PPT)
第 （三） 节
函数的单调性
一、知识体系
1、函数单调性的定义
2、单调性知识的应用
（1）、证明函数在指定区间的单调性
（2）、求函数的单调区间
（3）、求最值、值域、解不等式等等
（4）、涉及到抽象函数单调性问题的处理
（5）、利用单调性求解相关参数的问题
二、基础准备
1、函数单调性的
定义
在函数f(x)的定义域Ⅰ内，对于属于某个区间的任意两个自变量的值x1、x2,
①当x1②当x1f(x2),那么就说f(x)在这个区间上是减函数
③如果函数y=f(x)在某个区间是增函数或减函数，那么就说函数y=f(x)在这一区间具有(严格的)单调性
④这一区间叫做函数的单调区间
2、证明函数单调性的步骤是什么
证明函数单调性应该按下列步骤进行：
第一步：取值，设x1、x2是给定区间上的任意两个实数且x1则△x=x2-x1＞0
第二步：作差变形， f(x1)－f(x2) ，并将其变形到可以与0比较大小为止。
第三步：定号，f(x1)－f(x2)的正负
第四步：判断并下结论，如f(x1)－f(x2)<0即△y=f(x2)-f(x1)＞0,则f(x)在这个区间上是增函数
一、证明函数单调性
例1、证明函数 在 上是增函数
例2、判断函数f(x)=－x3+1在(－∞,0)上是增函数还是减函数，并证明你的结论；如果x∈（0，＋∞），函数f(x)是增函数还是减函数？
所以f(x)在(－∞,0)上是减函数
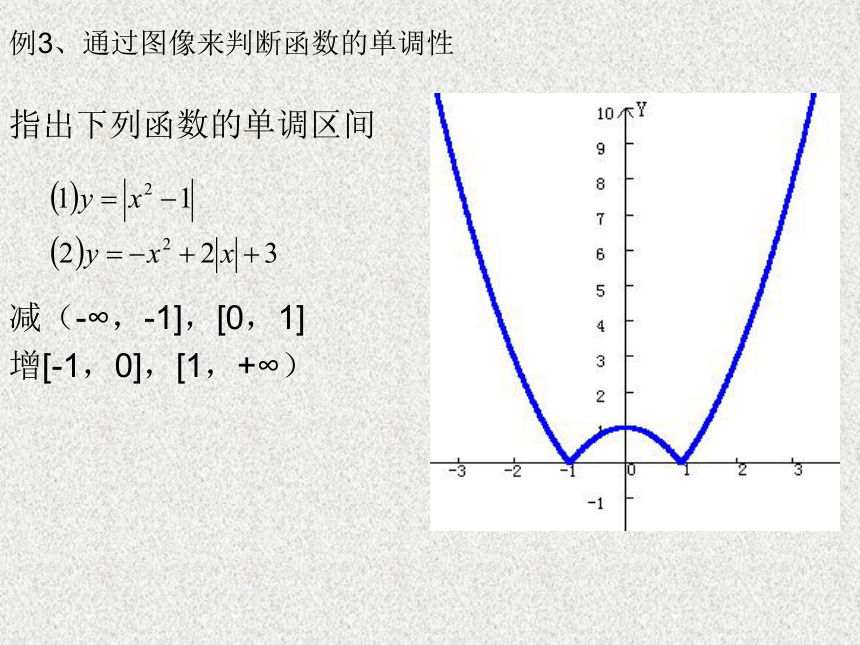
例3、通过图像来判断函数的单调性
指出下列函数的单调区间
减（-∞，-1]，[0，1]
增[-1，0]，[1，+∞）
(2)、y=-x2+2|x|+3
如果函数的图象比较好画，我们就画图象观察——图象法
增（-∞，-1），（0，1）
减（-1，0），（1，+∞）
利用图象法求单调区间的时候，应特别注意某些特殊点，尤其是图象发生急转弯的地方。用它们将定义域进行划分，再分别考察。
结论1：y＝f(x)(f(x) 恒不为0），与 的单调性相反。
二、利用已知函数单调性判断
例4：判断函数
在(1,+∞)上的单调性。
利用已知函数单调性进行判断
例5：设f(x)在定义域A上是减函数，试判断y＝3－2f(x)在A上的单调性，并说明理由。
解：y=3－2f(x)在A上是增函数，因为：
任取x1，x2∈A，且x1由f(x)在A上为减函数，所以
f(x1)>f(x2),故－2 f(x1)<－2f(x2) 所以3－2 f(x1)<3－2f(x2)即有
y1结论2：
y＝f(x)与y＝kf(x)
当k>0时，单调性相同；
当k<0时，单调性相反。
利用已知函数单调性进行判断
结论3：若f(x)与g(x)在R上是增函数，则f(x)+g(x)也是增函数。
结论4：若f(x) 在R上是增函数， g(x)在R上是减函数，则
f(x) －g(x)也是增函数
结论5：若f(x)(其中f(x)>0)在某个区间上为增函数，则
也是增函数
结论6：复合函数f[g(x)]由f(x)和g(x)的单调性共同决定。它们之间有如下关系：
f(x)
g(x)
f[g(x)]
例、 求函数 的单调区间
解: 记 ， ,列表如下:
(1)
(2)
即:原函数的增区间是（－∞，1];
减区间是[1，+∞）
利用已知函数单调性进行判断
练习：求函数
的单调区间。
答案：
(－∞, －3]单减区间
[2,+∞)单增区间
注意：求单调区间时，一定要先看定义域。
二、函数单调性解题应用
例6：已知函数
y=x2－2ax＋a2－1在(－∞,1)上是减函数，求a的取值范围。
解此类由二次函数单调性求参数范围的题，最好将二次函数的图象画出来，通过图象进行分析，可以将抽象的问题形象化。
练习：如果
f(x)=x2－(a－1)x+5在区间（0.5，1）上是增函数，那么
f(2)的取值范围是什么？
答案：[7,＋∞）
利用函数单调性解题（不等式）
例7：已知：f(x)是定义在[－1,1]上的增函数，且f(x－1)求x的取值范围。
注： 在利用函数的单调性解不等式的时候，一定要注意定义域的限制。
保证实施的是等价转化
利用函数单调性解题（抽象函数、不等式）
例8：已知f(x)在其定义域R＋上为增函数，
f(2)=1,f(xy)=f(x)+f(y).解不等式
f(x)+f(x－2) ≤3
解此类题型关键在于充分利用题目所给的条件，本题就抓住这点想办法构造出f(8)=3,这样就能用单调性解不等式了。
小结
1、怎样用定义证明函数的单调性？
2、判断函数的单调性有哪些方法？
3、与单调性有关的题型大致有哪些？
取值
作差
变形
定号
下结论
小结
1、怎样用定义证明函数的单调性？
2、判断函数的单调性有哪些方法？
3、与单调性有关的题型大致有哪些？
1、定义法
2、图象法
3、利用已知函数的单调性，通过一些简单结论、性质作出判断。
4、利用复合函数单调性的规则进行判断。
小结
1、怎样用定义证明函数的单调性？
2、判断函数的单调性有哪些方法？
3、与单调性有关的题型大致有哪些？
1、已知单调性，求参数范围。（有时候需要讨论）
3、利用单调性求解不等式。（重在转化问题）
2、利用函数单调性求函数的值域或最值。
4、求函数单调区间的题型（包括求复合函数单调区间）