轴对称过关测试题

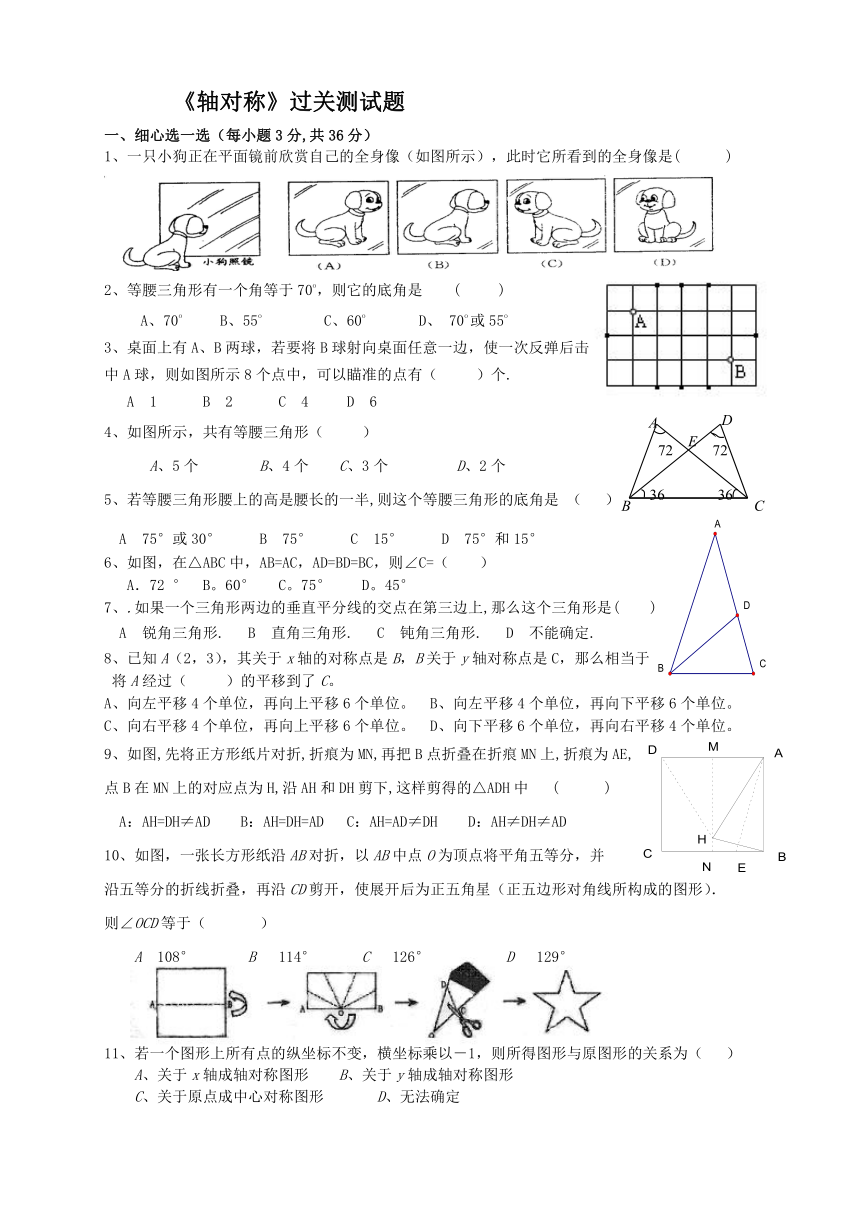
《轴对称》过关测试题
一、细心选一选（每小题3分,共36分）
1、一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时它所看到的全身像是( )
2、等腰三角形有一个角等于70o，则它的底角是 ( )
A、70o B、55o C、60o D、 70o或55o
3、桌面上有A、B两球，若要将B球射向桌面任意一边，使一次反弹后击
中A球，则如图所示8个点中，可以瞄准的点有（ ）个.
A 1 B 2 C 4 D 6
4、如图所示，共有等腰三角形（ ）
A、5个 B、4个 C、3个 D、2个
5、若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是 （ ）
A 75°或30° B 75° C 15° D 75°和15°
6、如图，在△ABC中，AB=AC，AD=BD=BC，则∠C=（ ）
A．72 ° B。60° C。75° D。45°
7、.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A 锐角三角形. B 直角三角形. C 钝角三角形. D 不能确定.
8、已知A（2，3），其关于x轴的对称点是B，B关于y轴对称点是C，那么相当于
将A经过（ ）的平移到了C。
A、向左平移4个单位，再向上平移6个单位。 B、向左平移4个单位，再向下平移6个单位。
C、向右平移4个单位，再向上平移6个单位。 D、向下平移6个单位，再向右平移4个单位。
9、如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,
点B在MN上的对应点为H,沿AH和DH剪下,这样剪得的△ADH中 ( )
A：AH=DH≠AD B：AH=DH=AD C：AH=AD≠DH D：AH≠DH≠AD
10、如图，一张长方形纸沿AB对折，以AB中点O为顶点将平角五等分，并
沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形）．
则∠OCD等于（ ）
A 108° B 114° C 126° D 129°
11、若一个图形上所有点的纵坐标不变，横坐标乘以－1，则所得图形与原图形的关系为（ ）
A、关于x轴成轴对称图形 B、关于y轴成轴对称图形
C、关于原点成中心对称图形 D、无法确定
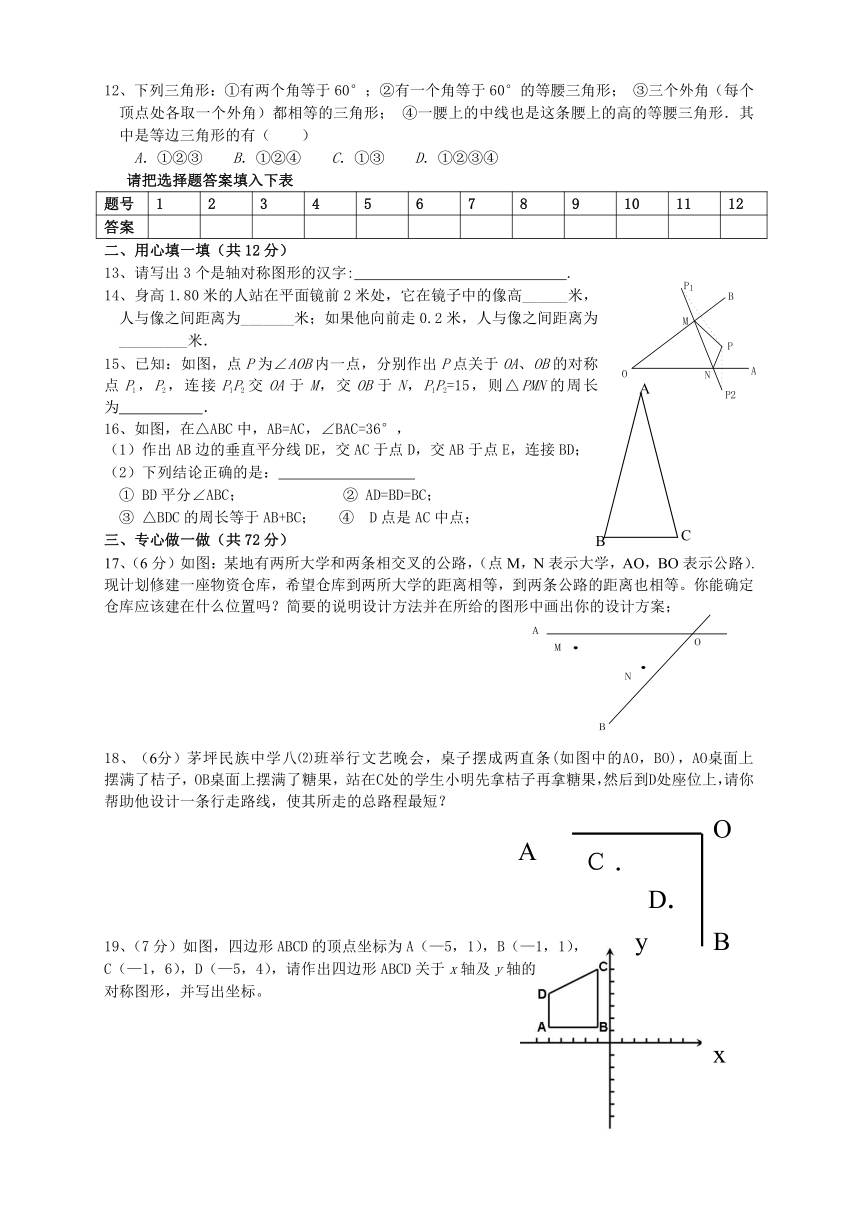
12、下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（ ）
A．①②③ B．①②④ C．①③ D．①②③④
请把选择题答案填入下表
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、用心填一填（共12分）
13、请写出3个是轴对称图形的汉字: .
14、身高1.80米的人站在平面镜前2米处，它在镜子中的像高______米，人与像之间距离为_______米；如果他向前走0.2米，人与像之间距离为_________米．
15、已知：如图，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=15，则△PMN的周长为 ．
16、如图，在△ABC中，AB=AC，∠BAC=36°，
（1）作出AB边的垂直平分线DE，交AC于点D，交AB于点E，连接BD；
（2）下列结论正确的是：
① BD平分∠ABC； ② AD=BD=BC；
③ △BDC的周长等于AB+BC； ④ D点是AC中点；
三、专心做一做（共72分）
17、（6分）如图：某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路）.现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等。你能确定仓库应该建在什么位置吗？简要的说明设计方法并在所给的图形中画出你的设计方案；
18、（6分）茅坪民族中学八⑵班举行文艺晚会，桌子摆成两直条(如图中的AO，BO)，AO桌面上摆满了桔子，OB桌面上摆满了糖果，站在C处的学生小明先拿桔子再拿糖果，然后到D处座位上，请你帮助他设计一条行走路线，使其所走的总路程最短？　
19、（7分）如图，四边形ABCD的顶点坐标为A（—5，1），B（—1，1），
C（—1，6），D（—5，4），请作出四边形ABCD关于x轴及y轴的
对称图形，并写出坐标。
20、（7分）如图，已知△ABC，∠CAE是△ABC的外角，在下列三项中：①AB=AC；②AD平分∠CAE；③AD∥BC．选择两项为题设，另一项为结论，组成一个真命题，并证明．
21、（7分）如图，已知：在Rt△ABC中，∠ACB=90°，∠B=30°，CD⊥AB于D
求证：AD=AB
22、（7分）如图所示，在等边三角形ABC中，∠ABC、∠ACB的平分线交于点O，OB和OC的垂直平分线交BC于E、F，试用你所学的知识说明BE=EF=FC的道理。
23、(10分)如图，点A、B、C在同一直线上，△ABD，△BCE都是等边三角形。
（1）求证：AE=CD；(4分)
（2）若M，N分别是AE，CD的中点，试判断△BMN的形状，并证明你的结论。(6分)
24、(10分)(1)、如图① △ABC中，BD=CD, ∠1=∠2, 求证：AB=AC（5分）
（2）、如图② BD=CD, ∠1=∠2, 此时 EB=AC是否成立吗？
请说明你的理由。(5分)
25、（12分）如图,△ABC是等腰直角三角形，，BC=AC，直角顶点C在x轴上，一锐角顶点B在y轴上。
（1）如图①，若点C的坐标是（2，0），点A的坐标是（-2，-2），求B点的坐标；（4分）
（2）如图②，若y轴恰好平分∠ABC，AC与y轴交与点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系，并说明理由。（4分）
（3）如图③，直角边BC在两坐标轴上滑动，使点A在第四象限内，过A点作AF⊥y轴于F，在滑动的过程中，两个结论①为定值；②为定值，只有一个结论成立，请你判断正确的结论加以证明并求出定值。（4分）
E
D
C
B
A
36°
36°
72°
72°
A
C
B
O
Ｃ． 。.
A
D.． 。.
y
B
x
A
B
C
D
E
B
A
C
E
D
N
M
①
②
①
②
③