人教版八年级上册数学教案:12.2.1全等三角形判定(SSS)
文档属性
| 名称 | 人教版八年级上册数学教案:12.2.1全等三角形判定(SSS) |  | |
| 格式 | zip | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-03 15:13:30 | ||
图片预览

文档简介
课题:§12.2.1
全等三角形的判定(SSS)
课标要求
掌握基本事实:三边分别相等的两个三角形全等.
教
学
目
标
知识技能
掌握边边边条件的内容;能初步应用边边边条件判定两个三角形全等.
数学思考
经历探索三角形全等条件的过程,体会用操作,归纳得出数量结论的过程
解决问题
会运用边边边条件证明两个三角全等
情感态度
通过探索三角形全等的条件的活动,培养学生合作交流的意识和大胆猜想,乐于探究的良好品质以及发现问题的能力.
重点
指导学生分析问题,寻找判定三角形全等的条件
难点
探究三角形全等的条件
学情
分析
学生在经历线段、角、相交线、平行线以及三角形的有关知识的学习,有了一点说理的基础,本节是研究的是两个图形之间的关系,可进一步引导学生学习推理论证的方法。
教法
演示、讲解
学法
动手操作、观察、合作探究
教具
圆规、三角形
教学程序设计
教学
环节
教学内容
师生活动
设计意图
一、
情境
引入
复习:已知△ABC
≌△
A′B′
C′,找出其中相等的边与角:
思考:满足这六个条件可以保证△ABC≌△A′B′C′吗?
追问1:当满足一个条件时,
△ABC
与△A′B′C′全等吗?
追问2:当满足两个条件时,
△ABC
与△A′B′C′全等吗?
追问3:当满足三个条件时,
△ABC
与△A′B′C′全等吗?满足三个条件时,又分为几种情况呢?
师出示复习,学生回答.
独立思考思考问题.
学生发现需要再分两种情况进行说明,即一条边分别相等、一个角分别相等.在探究过程中,可以通过画图加以说明,也可以利用三角尺等进行说明.
学生独立思考,教师适时点拨,最后达成共识:满足“两个条件”分两边、一边一角或两角分别相等三种情况.学生分三组分别进行探究,通过画图、展示交流,最后得出结论:只满足“两个条件”的两个三角形不一定全等.
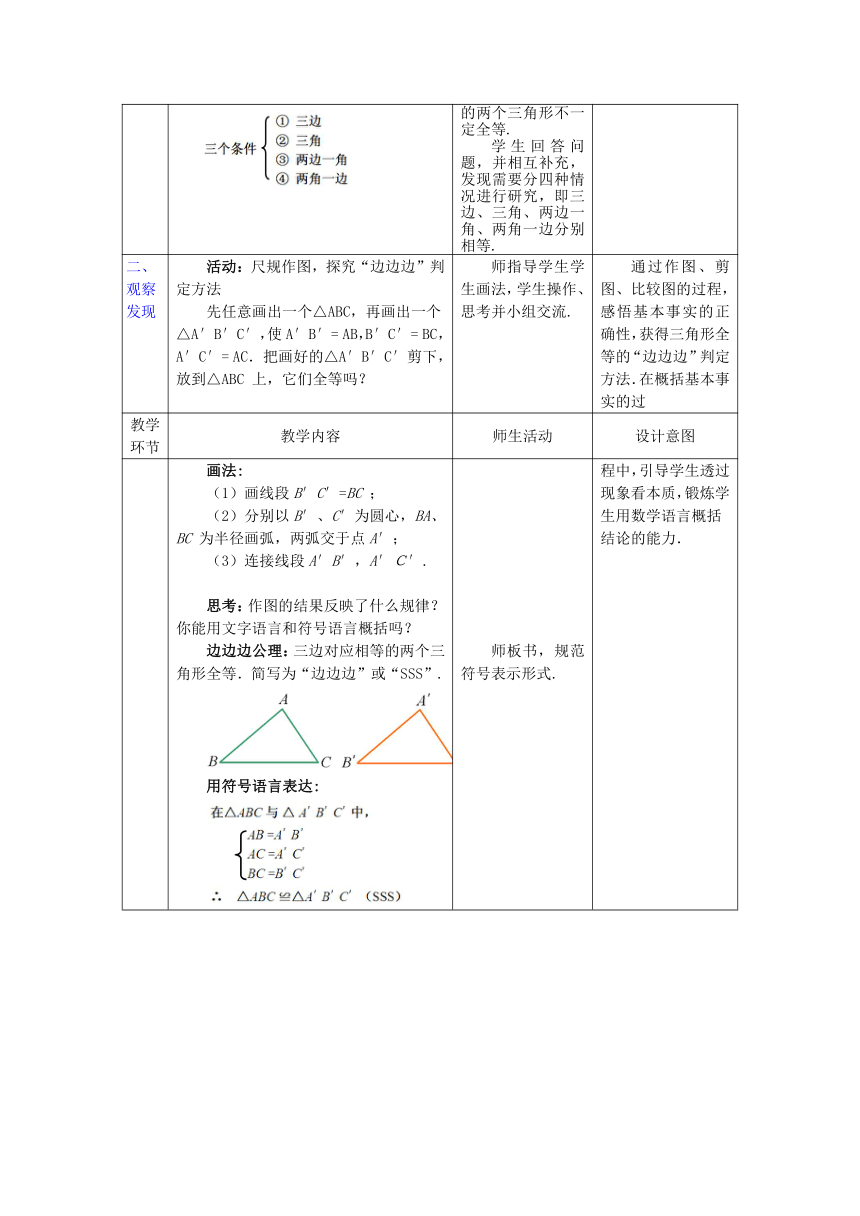
学生回答问题,并相互补充,发现需要分四种情况进行研究,即三边、三角、两边一角、两角一边分别相等.
先提出“全等判定”问题,构建出三角形全等条件的探索路径,然后以问题串的方式呈现探究过程,引导学生层层深入地思考问题.
二、
观察
发现
活动:尺规作图,探究“边边边”判定方法
先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′=
AB,B′C′=
BC,A′C′=
AC.把画好的△A′B′C′剪下,放到△ABC
上,它们全等吗?
师指导学生学生画法,学生操作、思考并小组交流.
通过作图、剪图、比较图的过程,感悟基本事实的正确性,获得三角形全等的“边边边”判定方法.在概括基本事实的过
教学
环节
教学内容
师生活动
设计意图
画法:
(1)画线段B′C′=BC
;
(2)分别以B′、C′为圆心,BA、BC
为半径画弧,两弧交于点A′;
(3)连接线段A′B′,A′C′.
思考:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
边边边公理:三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
用符号语言表达:
师板书,规范符号表示形式.
程中,引导学生透过现象看本质,锻炼学生用数学语言概括结论的能力.
三、
应用
提高
问题:我们曾经做过这样的实验:将三根木条钉成一个三角形木架,这个三角形木架的形状、大小就不变了.你能解释其中的道理吗?
例1:如图所示的三角形钢架中,AB
=AC
,AD
是连接点A
与BC
中点D
的支架.求证△ABD
≌△ACD
.
应用:用尺规作一个角等于已知角.
已知:∠AOB.
求作:
∠A′O′B′=∠AOB.
学生用“边边边”判定方法进行解释.
师生共同分析解题思路,即要证明两三角形全等,就要看这两个三角形的三条边是否分别相等,题中有一个隐含条件AD是两个三角形的公共边.学生口述证明过程,教师板书.
师指导学生用尺规作图.
用所学知识解释生活现象,进一步体会判定方法的作用,感悟数学的应用价值.
运用“边边边”判定方法证明简单的几何问题,感悟判定方法的简捷性,体会证明过程的规范性.
让学生运用“SSS”条件进行尺规作图,同时体会作图的合理性,增强作图技能.
四、
巩固
练习
练习:
1.课本P37页练习第1、2题
2.
如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
学生观察图形后,寻找全等的三角形,同时注意引导学生考虑到特殊位置时结论的正确性.
运用数学知识解决实际问题.采用小组合作探究的方式,这样既培养了学生的合作精神,又培养了学生发散思维和创新思维的能力.
教学
环节
教学内容
师生活动
设计意图
五、
体验
收获
谈谈你的收获和体会
师引导学生回答,并补充完善.
通过小结,使学生梳理本节课所学内容,掌握本节课的核心—构建三角形全等条件的探索思路,以及判定三角形全等的“边边边”方法.
六、
实践
延伸
课后作业:
课本P43页习题12.2第1、9题.
学生课后独立完成.
检测学生对本节所学知识的掌握情况.
附:板书设计
全等三角形的判定(SSS)
课标要求
掌握基本事实:三边分别相等的两个三角形全等.
教
学
目
标
知识技能
掌握边边边条件的内容;能初步应用边边边条件判定两个三角形全等.
数学思考
经历探索三角形全等条件的过程,体会用操作,归纳得出数量结论的过程
解决问题
会运用边边边条件证明两个三角全等
情感态度
通过探索三角形全等的条件的活动,培养学生合作交流的意识和大胆猜想,乐于探究的良好品质以及发现问题的能力.
重点
指导学生分析问题,寻找判定三角形全等的条件
难点
探究三角形全等的条件
学情
分析
学生在经历线段、角、相交线、平行线以及三角形的有关知识的学习,有了一点说理的基础,本节是研究的是两个图形之间的关系,可进一步引导学生学习推理论证的方法。
教法
演示、讲解
学法
动手操作、观察、合作探究
教具
圆规、三角形
教学程序设计
教学
环节
教学内容
师生活动
设计意图
一、
情境
引入
复习:已知△ABC
≌△
A′B′
C′,找出其中相等的边与角:
思考:满足这六个条件可以保证△ABC≌△A′B′C′吗?
追问1:当满足一个条件时,
△ABC
与△A′B′C′全等吗?
追问2:当满足两个条件时,
△ABC
与△A′B′C′全等吗?
追问3:当满足三个条件时,
△ABC
与△A′B′C′全等吗?满足三个条件时,又分为几种情况呢?
师出示复习,学生回答.
独立思考思考问题.
学生发现需要再分两种情况进行说明,即一条边分别相等、一个角分别相等.在探究过程中,可以通过画图加以说明,也可以利用三角尺等进行说明.
学生独立思考,教师适时点拨,最后达成共识:满足“两个条件”分两边、一边一角或两角分别相等三种情况.学生分三组分别进行探究,通过画图、展示交流,最后得出结论:只满足“两个条件”的两个三角形不一定全等.
学生回答问题,并相互补充,发现需要分四种情况进行研究,即三边、三角、两边一角、两角一边分别相等.
先提出“全等判定”问题,构建出三角形全等条件的探索路径,然后以问题串的方式呈现探究过程,引导学生层层深入地思考问题.
二、
观察
发现
活动:尺规作图,探究“边边边”判定方法
先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′=
AB,B′C′=
BC,A′C′=
AC.把画好的△A′B′C′剪下,放到△ABC
上,它们全等吗?
师指导学生学生画法,学生操作、思考并小组交流.
通过作图、剪图、比较图的过程,感悟基本事实的正确性,获得三角形全等的“边边边”判定方法.在概括基本事实的过
教学
环节
教学内容
师生活动
设计意图
画法:
(1)画线段B′C′=BC
;
(2)分别以B′、C′为圆心,BA、BC
为半径画弧,两弧交于点A′;
(3)连接线段A′B′,A′C′.
思考:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
边边边公理:三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
用符号语言表达:
师板书,规范符号表示形式.
程中,引导学生透过现象看本质,锻炼学生用数学语言概括结论的能力.
三、
应用
提高
问题:我们曾经做过这样的实验:将三根木条钉成一个三角形木架,这个三角形木架的形状、大小就不变了.你能解释其中的道理吗?
例1:如图所示的三角形钢架中,AB
=AC
,AD
是连接点A
与BC
中点D
的支架.求证△ABD
≌△ACD
.
应用:用尺规作一个角等于已知角.
已知:∠AOB.
求作:
∠A′O′B′=∠AOB.
学生用“边边边”判定方法进行解释.
师生共同分析解题思路,即要证明两三角形全等,就要看这两个三角形的三条边是否分别相等,题中有一个隐含条件AD是两个三角形的公共边.学生口述证明过程,教师板书.
师指导学生用尺规作图.
用所学知识解释生活现象,进一步体会判定方法的作用,感悟数学的应用价值.
运用“边边边”判定方法证明简单的几何问题,感悟判定方法的简捷性,体会证明过程的规范性.
让学生运用“SSS”条件进行尺规作图,同时体会作图的合理性,增强作图技能.
四、
巩固
练习
练习:
1.课本P37页练习第1、2题
2.
如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
学生观察图形后,寻找全等的三角形,同时注意引导学生考虑到特殊位置时结论的正确性.
运用数学知识解决实际问题.采用小组合作探究的方式,这样既培养了学生的合作精神,又培养了学生发散思维和创新思维的能力.
教学
环节
教学内容
师生活动
设计意图
五、
体验
收获
谈谈你的收获和体会
师引导学生回答,并补充完善.
通过小结,使学生梳理本节课所学内容,掌握本节课的核心—构建三角形全等条件的探索思路,以及判定三角形全等的“边边边”方法.
六、
实践
延伸
课后作业:
课本P43页习题12.2第1、9题.
学生课后独立完成.
检测学生对本节所学知识的掌握情况.
附:板书设计
