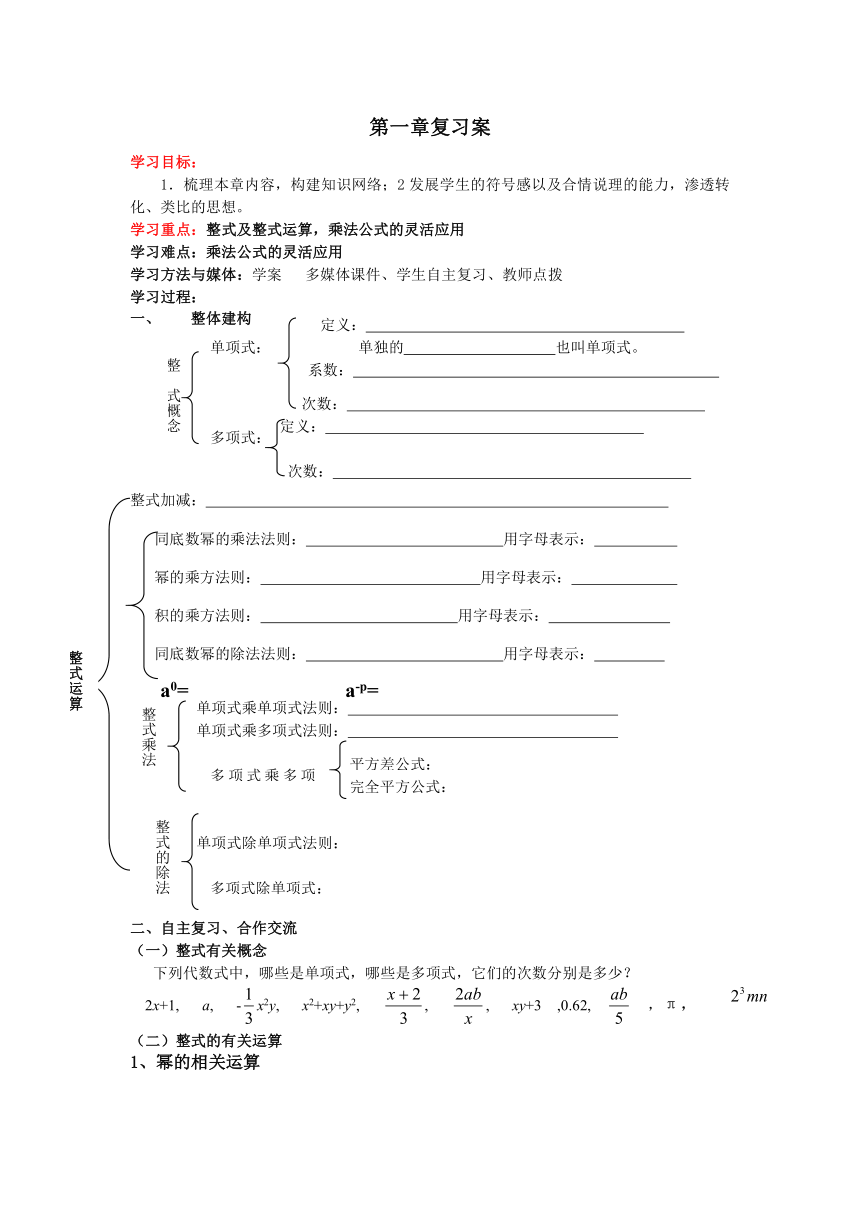
第一章复习案

第一章复习案
学习目标：
1．梳理本章内容，构建知识网络；2发展学生的符号感以及合情说理的能力，渗透转化、类比的思想。
学习重点：整式及整式运算，乘法公式的灵活应用
学习难点：乘法公式的灵活应用
学习方法与媒体：学案 多媒体课件、学生自主复习、教师点拨
学习过程：
整体建构
整式加减：
a0= a-p=
二、自主复习、合作交流
（一）整式有关概念
下列代数式中，哪些是单项式，哪些是多项式，它们的次数分别是多少？
2x+1, a, -x2y, x2+xy+y2, , , xy+3 ,0.62, ，π，
（二）整式的有关运算
1、幂的相关运算
= = = =
2、整式加减乘除运算
(1)、5x2-[3x-2(2x-3)-4x2] (2)
(3)-5a（2a2-3a+4） ( 4 )
(5)、－６xy÷（２xy）(6)、（-15x2y-10xy2）÷（-5xy）
易错点：
3、乘法公式及应用
(1)、(y+3z)(y-3z) ( 2)、 (-2b- 5) (2b -5)
(3)、103×97 （4）(-m-2)2 ； （5）(-8x+3)2
（6）9982 （7）(2x+3)（4x+9）（2x-3） (8)(x-y+1)(x+y-1)
易错点：
三、当堂练习：
典例分析
例1
1、若要使是完全平方式，则m的值应为（ ）。
A． 　　　　　 B． 　C． 　　　　D．
2、（2）如果多项式是一个完全平方式，则k的值是（ ）
A、－4 B、4 C、－16 D、16
例2：若的积不含x的一次项，求a的值。
例3
求值
1、，其中，
2、（2a+2b+1）（2a+2b-1）=63，求a+b的值。
思维拓展：
已知：
四、当堂达标：
A
B
（2）如果关于字母x多项式3mx2-x2+6xy-4y-2(4x2+3xy+4)的值与x无关.求多项式m2-[m2+(3m-4)+m]的值.
课后达标
A(1) 4a2c5 (-3a3bc2) (2) (x2y-2xy+y2)(-3xy)
(3) (3a–2)(a–1)–(a+1)(a+2) （4）（3x-6）(3x+6)
（5） (28a-14a+7a)÷7 （6）（2x-1）（1-2x）
（7）（3a-4b）-（2a-b） （8）（3a-4b）·（-4b-3a）
B
（1） x+y=-5，xy=3，求x+y及（x-y）2的值。
(2)其中
(3)如果a =2，a =3 ，求 a ，a
定义：
单独的 也叫单项式。
单项式：
整 式概念
系数：
次数：
定义：
多项式：
次数：
同底数幂的乘法法则： 用字母表示：
幂的乘方法则： 用字母表示：
积的乘方法则： 用字母表示：
多项式乘多项式
同底数幂的除法法则： 用字母表示：
整式运算
整式乘法
单项式乘单项式法则：
单项式乘多项式法则：
平方差公式：
完全平方公式：
整式的除法
单项式除单项式法则：
多项式除单项式：
m-2n
2m+3n
m
n