2021中考数学备考经典微专题 反比例函数中k的几何意义的应用 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 反比例函数中k的几何意义的应用 学案(技巧+满分解答) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 08:31:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
反比例函数中的几何意义的应用
如图1,在平面直角坐标系中,在反比例函数图象上任取一点,作轴,轴,垂足为,,则
这个结论就是我们通常所说的“的几何意义”.本文通过举例说明的几何意义的应用.
一、求的值
例1 如图2,经过原点的直线交反比例函数的图象于,两点,轴于点.若面积为6,则的值是 .
解析 因为反比例函数的图象关于原点对称,直线经过原点,且与反比例
函数的图象交于,两点,所以,两点关于原点对称.于是,所以的面积等于面积的一半,即,根据的几何意义,,又因为反比例函数的图象位于第一、三象限,故.
二求图形面积
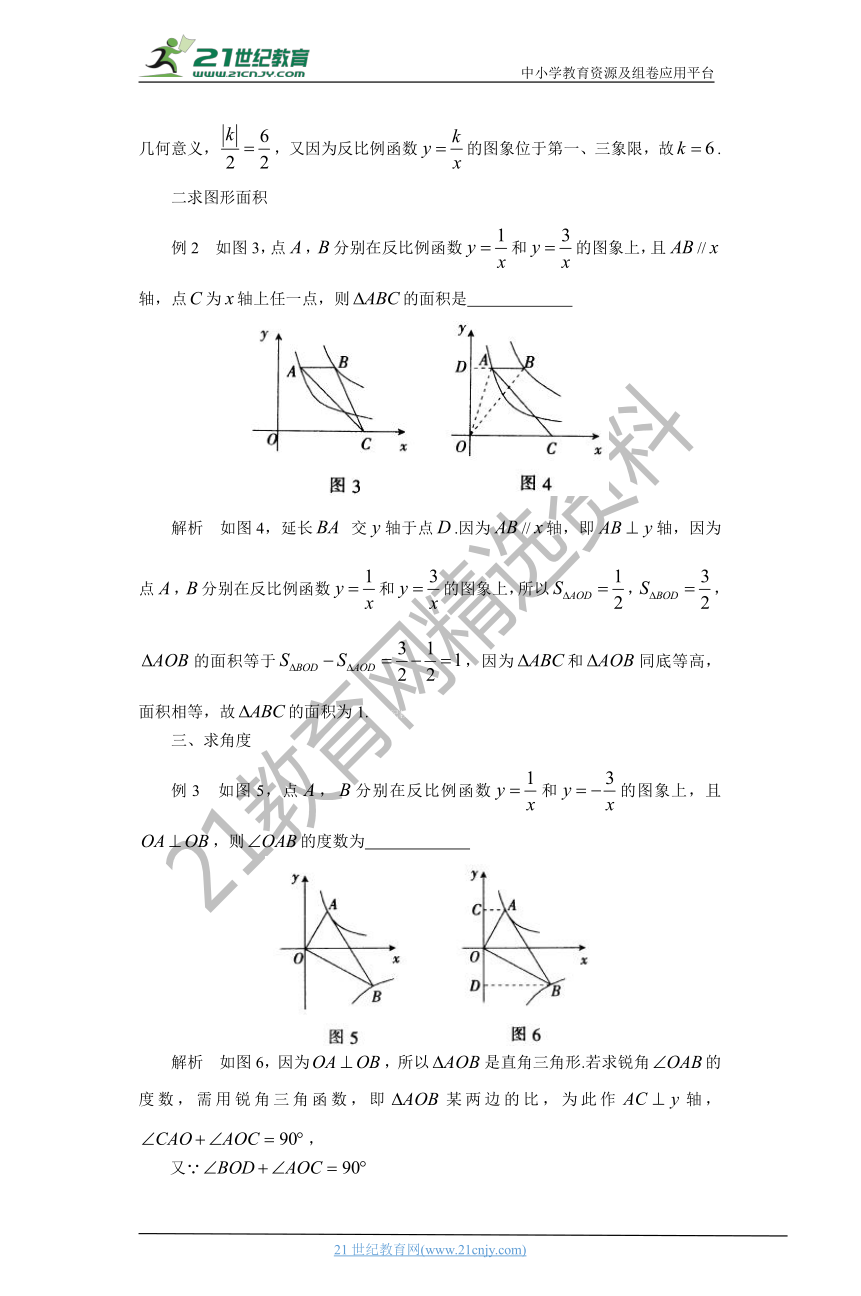
例2 如图3,点,分别在反比例函数和的图象上,且//轴,点为轴上任一点,则的面积是
解析 如图4,延长 交轴于点.因为//轴,即轴,因为点,分别在反比例函数和的图象上,所以,,的面积等于,因为和同底等高,面积相等,故的面积为1.21世纪教育网版权所有
三、求角度
例3 如图5,点,分别在反比例函数和的图象上,且,则的度数为 21cnjy.com
解析 如图6,因为,所以是直角三角形.若求锐角的度数,需用锐角三角函数,即某两边的比,为此作轴,,
又
根据的几何意义
,
四比较图形面积大小
例4 如图7,已知,,、在轴上,顶点,在反比例函数图象上,斜边,分别交轴于点,.若四边形和四边形的面积分别是,则( )21教育网
(A ) >
(B) =
(C ) <
(D) ,的大小关系不能确定
解析 分别过点, 作轴的垂线,垂足为,,根据的几何意义,矩形与矩形面积相等,即E .
设,
则
,
,
而
故四边形和四边形的面积相等,即=,应选B
五、证明结论
例5已知点,为反比例函数图象上两点,直线与:轴、轴分别交于点,,则.
解析 若,点,可能在同一象限(如图8),也可能位于不同象限(如图9),下
面只给出后一种情形的证明.
过点分别作轴,轴,垂足为,,过点分别作轴,轴,垂足为,,,相交于点.根据的几何意义可知,矩形与矩形的面积相等(等于),
,
//
所以四边形和四边形都是平行四边形,
故
若,证明方法相同.
_21?????????è?????(www.21cnjy.com)_
反比例函数中的几何意义的应用
如图1,在平面直角坐标系中,在反比例函数图象上任取一点,作轴,轴,垂足为,,则
这个结论就是我们通常所说的“的几何意义”.本文通过举例说明的几何意义的应用.
一、求的值
例1 如图2,经过原点的直线交反比例函数的图象于,两点,轴于点.若面积为6,则的值是 .
解析 因为反比例函数的图象关于原点对称,直线经过原点,且与反比例
函数的图象交于,两点,所以,两点关于原点对称.于是,所以的面积等于面积的一半,即,根据的几何意义,,又因为反比例函数的图象位于第一、三象限,故.
二求图形面积
例2 如图3,点,分别在反比例函数和的图象上,且//轴,点为轴上任一点,则的面积是
解析 如图4,延长 交轴于点.因为//轴,即轴,因为点,分别在反比例函数和的图象上,所以,,的面积等于,因为和同底等高,面积相等,故的面积为1.21世纪教育网版权所有
三、求角度
例3 如图5,点,分别在反比例函数和的图象上,且,则的度数为 21cnjy.com
解析 如图6,因为,所以是直角三角形.若求锐角的度数,需用锐角三角函数,即某两边的比,为此作轴,,
又
根据的几何意义
,
四比较图形面积大小
例4 如图7,已知,,、在轴上,顶点,在反比例函数图象上,斜边,分别交轴于点,.若四边形和四边形的面积分别是,则( )21教育网
(A ) >
(B) =
(C ) <
(D) ,的大小关系不能确定
解析 分别过点, 作轴的垂线,垂足为,,根据的几何意义,矩形与矩形面积相等,即E .
设,
则
,
,
而
故四边形和四边形的面积相等,即=,应选B
五、证明结论
例5已知点,为反比例函数图象上两点,直线与:轴、轴分别交于点,,则.
解析 若,点,可能在同一象限(如图8),也可能位于不同象限(如图9),下
面只给出后一种情形的证明.
过点分别作轴,轴,垂足为,,过点分别作轴,轴,垂足为,,,相交于点.根据的几何意义可知,矩形与矩形的面积相等(等于),
,
//
所以四边形和四边形都是平行四边形,
故
若,证明方法相同.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
