2021中考数学备考经典微专题 活用中点构造全等三角形 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 活用中点构造全等三角形 学案(技巧+满分解答) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 08:43:22 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
活用中点构造全等三角形
《中小学数学课程标准》指出,在数学教学中,要重视学生对所学知识的反思,利用分层次和多样化的训练,特别重视变式训练,让学生能够懂得从特殊到一般、从一般到特殊以及转化等思维策略.
本文就等腰三角形“三线合一定理”作拓展探索研究.
“三线合一”定理,即等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
已知:如图1,中,,求证:的中线、高和平分线互相重合.
证明 作底边的中线.
,,是公共边,
的中线、高和平分线互相重合.
变式1 (条件之间的变化)如图1,中是的中线,,求证:[来源:Z§xx§k.Com]
证明 延长线段到点,使.
,,
,
变式2 (图形变化)如图2,已知,,求证:
证明 延长线段到点,使.
,,
,
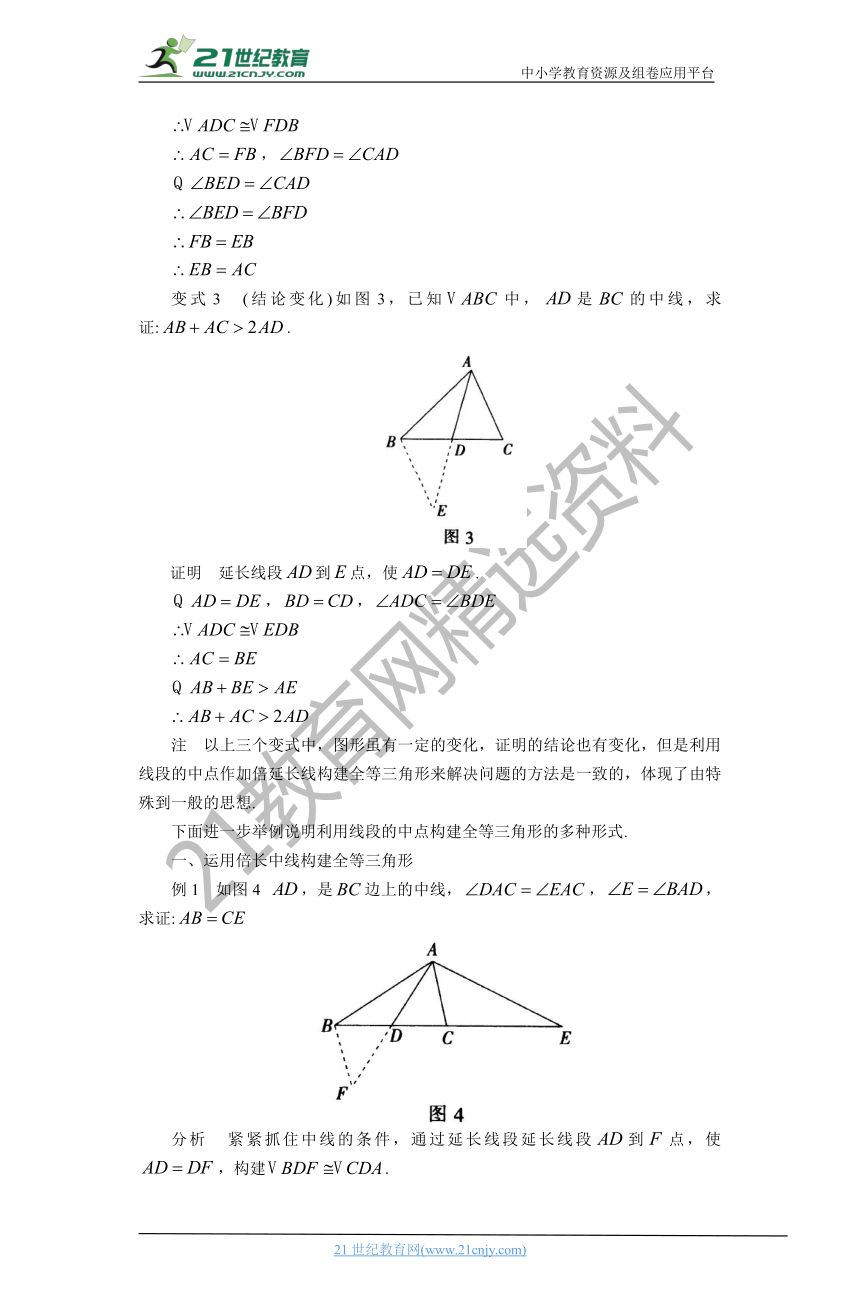
变式3 (结论变化)如图3,已知中,是的中线,求证:.
证明 延长线段到点,使.
,,
注 以上三个变式中,图形虽有一定的变化,证明的结论也有变化,但是利用线段的中点作加倍延长线构建全等三角形来解决问题的方法是一致的,体现了由特殊到一般的思想.
下面进一步举例说明利用线段的中点构建全等三角形的多种形式.[来源:学_科_网Z_X_X_K]
一、运用倍长中线构建全等三角形
例1 如图4 ,是边上的中线,,,求证:
分析 紧紧抓住中线的条件,通过延长线段延长线段到点,使,构建.
证明 延长线段到点,使.
,,
,
,
二、运用作平行线构建全等三角形
例2 如图5,已知,,求证:.
分析 本题若直接证明,会发现对应边不对.而抓住中线的条件,如何作辅助线是关键.本题只提供了一个角的条件,如果作延长线,则会破坏和,而过点作,则可以得到.
证明 过点作交于点.
,
三、运用模型构建全等三角形
例3 如图6,已知,,,交于点,连结,求证:.
分析 此题可借鉴下列由直角和直角构成的模型(见图7(1)~图7(5):
证明 如图6,过点作,交的延长线于点.
,
,
,
,,是公共边,
数学是研究数量关系和空间形式的科学.学生通过数学学习,掌握数学的基础知识、基本技能和思想方法,学会有条理地思考和简明清晰地表达思考过程,并运用数学的思想方法分析问题和解决问题,能培养学生的抽象能力、推理能力、创造能力.我们在教学过程中,要让学生体会到数学之美,做到授生以渔,而非授生以鱼,就能在数学教学中达到事半功倍的效果.
_21?????????è?????(www.21cnjy.com)_
活用中点构造全等三角形
《中小学数学课程标准》指出,在数学教学中,要重视学生对所学知识的反思,利用分层次和多样化的训练,特别重视变式训练,让学生能够懂得从特殊到一般、从一般到特殊以及转化等思维策略.
本文就等腰三角形“三线合一定理”作拓展探索研究.
“三线合一”定理,即等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
已知:如图1,中,,求证:的中线、高和平分线互相重合.
证明 作底边的中线.
,,是公共边,
的中线、高和平分线互相重合.
变式1 (条件之间的变化)如图1,中是的中线,,求证:[来源:Z§xx§k.Com]
证明 延长线段到点,使.
,,
,
变式2 (图形变化)如图2,已知,,求证:
证明 延长线段到点,使.
,,
,
变式3 (结论变化)如图3,已知中,是的中线,求证:.
证明 延长线段到点,使.
,,
注 以上三个变式中,图形虽有一定的变化,证明的结论也有变化,但是利用线段的中点作加倍延长线构建全等三角形来解决问题的方法是一致的,体现了由特殊到一般的思想.
下面进一步举例说明利用线段的中点构建全等三角形的多种形式.[来源:学_科_网Z_X_X_K]
一、运用倍长中线构建全等三角形
例1 如图4 ,是边上的中线,,,求证:
分析 紧紧抓住中线的条件,通过延长线段延长线段到点,使,构建.
证明 延长线段到点,使.
,,
,
,
二、运用作平行线构建全等三角形
例2 如图5,已知,,求证:.
分析 本题若直接证明,会发现对应边不对.而抓住中线的条件,如何作辅助线是关键.本题只提供了一个角的条件,如果作延长线,则会破坏和,而过点作,则可以得到.
证明 过点作交于点.
,
三、运用模型构建全等三角形
例3 如图6,已知,,,交于点,连结,求证:.
分析 此题可借鉴下列由直角和直角构成的模型(见图7(1)~图7(5):
证明 如图6,过点作,交的延长线于点.
,
,
,
,,是公共边,
数学是研究数量关系和空间形式的科学.学生通过数学学习,掌握数学的基础知识、基本技能和思想方法,学会有条理地思考和简明清晰地表达思考过程,并运用数学的思想方法分析问题和解决问题,能培养学生的抽象能力、推理能力、创造能力.我们在教学过程中,要让学生体会到数学之美,做到授生以渔,而非授生以鱼,就能在数学教学中达到事半功倍的效果.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
