2021中考数学备考经典微专题 基本图形在中考几何中的应用 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 基本图形在中考几何中的应用 学案(技巧+满分解答) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 08:53:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
基本图形在中考几何中的应用
我们知道,教材中所选_???é??????????????_都是经过专家深思熟虑、精心筛选的,不少图形具有典型性和代表性,其性质的应用具有一般性,我们常把这些图形称为基本图形.如果我们在解题中能联想到这些基本图形及其性质,就能开启我们的解题思路,使问题得到快速、正确的解答.下面以中考真题为例说明.
例1 如图1,是的高,,求.
解 是的高,
在中,
.
在中,
,
.
例2 如图2,在中,,求.
解 过点作,垂足为,
则.
在中,
,
在中,
,
.
例3 如图3,平地上一幢建筑物与铁塔相距60m,在建筑物的顶部测得铁塔底部的俯角为,测得铁塔顶部的仰角为,求铁塔的高度(精确到lm).
解 过点作于点,如图3,则四边形为矩形,
.
在中,
.
在中,
,
,
.
答:铁塔的高度约为95米.
上述图1中的、图2中的、图3中的都是非直角三角形,但在解题中可通过添加辅助线(作高),将其转化为直角三角形求解.教材在这一章编排时出现了3次类似的图形和问题,从易到难、逐步加深,目的就是说明这个图形的重要性,我们要深刻掌握其中“化斜为直”的解题方法.下面请看近几年各地中考题中利用基本图形解决问题的例子.
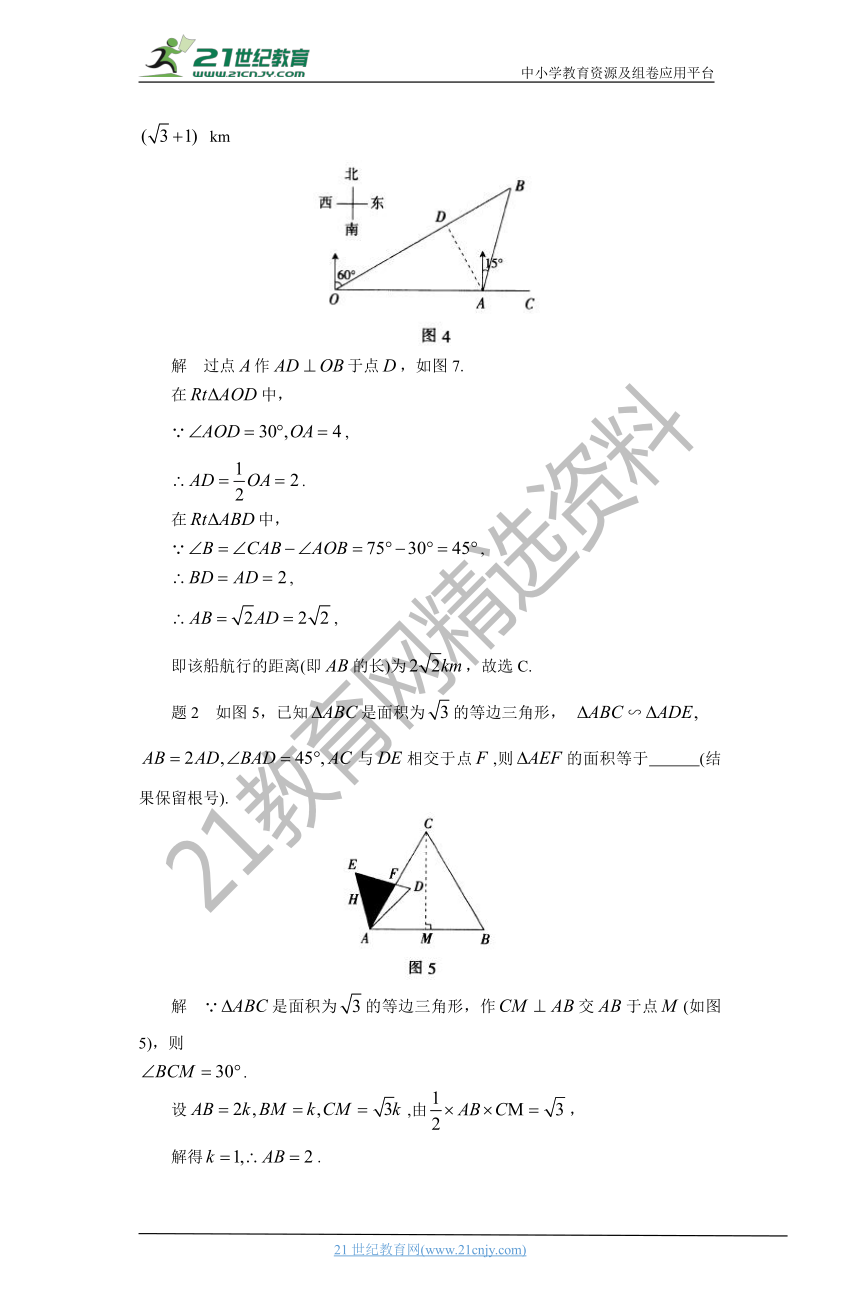
题1 如图4,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船航行的距离(即的长)为( )
(A) 4km (B) km (C) km (D) km
解 过点作于点,如图7.
在中,
,
.
在中,
,
,
,
即该船航行的距离(即的长)为,故选C.
题2 如图5,已知是面积为的等边三角形, ∽
与相交于点,则的面积等于 (结果保留根号).
解 是面积为的等边三角形,作交于点(如图5),则
.
设,由,
解得.
.
过点作交于点,如图5.
∽,
,
.
设,
则.
,
解得.
.
题3 如图6,在一笔直的海岸线上有两个观测站,在的正东方向,(单位:km).有一艘小船在点处,从测得小船在北偏西的方向,从测得小船在北偏东的方向.
(1)求点到海岸线的距离;
(2)小船从点处沿射线的方向航行一段时间后,到点处,此时,从测得小船在北偏西的方向,求点与点之间的距离.(上述两小题的结果都保留根号)
解 (1)过点作于点,如图6.设 km,由题意,可知
,
在中, .
在中, .
.
答:点到海岸线的距离为()km.
(2)如图6,过点作于点.
在中,.
在中,.
在中, .
答:点与点之间的距离为km.
题4 如图7,已知.按如下步骤作图:①以为圆心,长为半径
画弧;②以为圆心,长为半径画弧,两弧相交于点;③连结,与交于点,连结.若,求的长.
解
≌.
,
,即.
在中,
.
在中,
.
,
,
解得.
题5 如图8,四边形与四边形都是菱形,其中点在上,点分别在上,若,则= .
解 ,四边形与四边形都是菱形,
,
.
过点作于点,如图8,设,在中,
,
.
在中,
.
则.
题6 已知:如图9,在中,是边上一点,圆过三点, .(1)求证:直线是圆的切线;(2)如果,圆的半径为2,求的长.
解 (1),
.
,
,
,
直线是圆的切线.
(2) ,
.
,
.
作于点,如图9,
则,
.
.
_21?????????è?????(www.21cnjy.com)_
基本图形在中考几何中的应用
我们知道,教材中所选_???é??????????????_都是经过专家深思熟虑、精心筛选的,不少图形具有典型性和代表性,其性质的应用具有一般性,我们常把这些图形称为基本图形.如果我们在解题中能联想到这些基本图形及其性质,就能开启我们的解题思路,使问题得到快速、正确的解答.下面以中考真题为例说明.
例1 如图1,是的高,,求.
解 是的高,
在中,
.
在中,
,
.
例2 如图2,在中,,求.
解 过点作,垂足为,
则.
在中,
,
在中,
,
.
例3 如图3,平地上一幢建筑物与铁塔相距60m,在建筑物的顶部测得铁塔底部的俯角为,测得铁塔顶部的仰角为,求铁塔的高度(精确到lm).
解 过点作于点,如图3,则四边形为矩形,
.
在中,
.
在中,
,
,
.
答:铁塔的高度约为95米.
上述图1中的、图2中的、图3中的都是非直角三角形,但在解题中可通过添加辅助线(作高),将其转化为直角三角形求解.教材在这一章编排时出现了3次类似的图形和问题,从易到难、逐步加深,目的就是说明这个图形的重要性,我们要深刻掌握其中“化斜为直”的解题方法.下面请看近几年各地中考题中利用基本图形解决问题的例子.
题1 如图4,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船航行的距离(即的长)为( )
(A) 4km (B) km (C) km (D) km
解 过点作于点,如图7.
在中,
,
.
在中,
,
,
,
即该船航行的距离(即的长)为,故选C.
题2 如图5,已知是面积为的等边三角形, ∽
与相交于点,则的面积等于 (结果保留根号).
解 是面积为的等边三角形,作交于点(如图5),则
.
设,由,
解得.
.
过点作交于点,如图5.
∽,
,
.
设,
则.
,
解得.
.
题3 如图6,在一笔直的海岸线上有两个观测站,在的正东方向,(单位:km).有一艘小船在点处,从测得小船在北偏西的方向,从测得小船在北偏东的方向.
(1)求点到海岸线的距离;
(2)小船从点处沿射线的方向航行一段时间后,到点处,此时,从测得小船在北偏西的方向,求点与点之间的距离.(上述两小题的结果都保留根号)
解 (1)过点作于点,如图6.设 km,由题意,可知
,
在中, .
在中, .
.
答:点到海岸线的距离为()km.
(2)如图6,过点作于点.
在中,.
在中,.
在中, .
答:点与点之间的距离为km.
题4 如图7,已知.按如下步骤作图:①以为圆心,长为半径
画弧;②以为圆心,长为半径画弧,两弧相交于点;③连结,与交于点,连结.若,求的长.
解
≌.
,
,即.
在中,
.
在中,
.
,
,
解得.
题5 如图8,四边形与四边形都是菱形,其中点在上,点分别在上,若,则= .
解 ,四边形与四边形都是菱形,
,
.
过点作于点,如图8,设,在中,
,
.
在中,
.
则.
题6 已知:如图9,在中,是边上一点,圆过三点, .(1)求证:直线是圆的切线;(2)如果,圆的半径为2,求的长.
解 (1),
.
,
,
,
直线是圆的切线.
(2) ,
.
,
.
作于点,如图9,
则,
.
.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
