2021中考数学备考经典微专题 解决动点生成的函数图象压轴选择题 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 解决动点生成的函数图象压轴选择题 学案(技巧+满分解答) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
解决动点生成的函数图象压轴选择题
由动点生成的函数图_è±?é??é????????è??_几年中考的热点问题.此类问题多出现在选择压轴题中,可见其分量,因此不少学生往往是望而却步.笔者通过研究发现,抓住“两点”,可以使该类问题轻松获解,下面略举几例与大家分享.
一、抓住“拐点”
这里所说的“拐点”指的是,动点经过多边形的顶点时,生成的函数图象不平滑,即出了“尖”,我们称之为“拐点”.
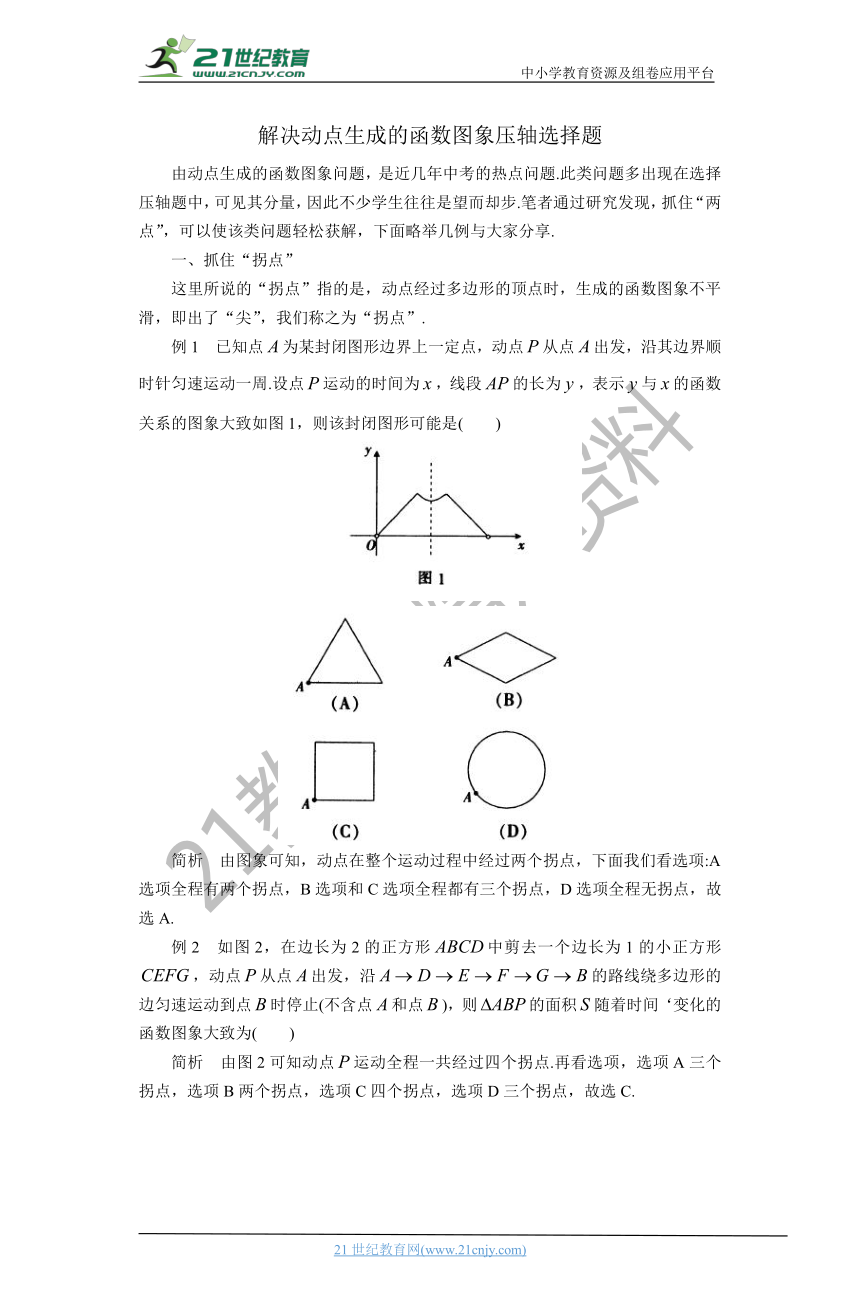
例1 已知点为某封闭图形边界上一定点,动点从点出发,沿其边界顺时针匀速运动一周.设点运动的时间为,线段的长为,表示与的函数关系的图象大致如图1,则该封闭图形可能是( )
简析 由_???è±????????????¨_点在整个运动过程中经过两个拐点,下面我们看选项:A选项全程有两个拐点,B选项和C选项全程都有三个拐点,D选项全程无拐点,故选A.
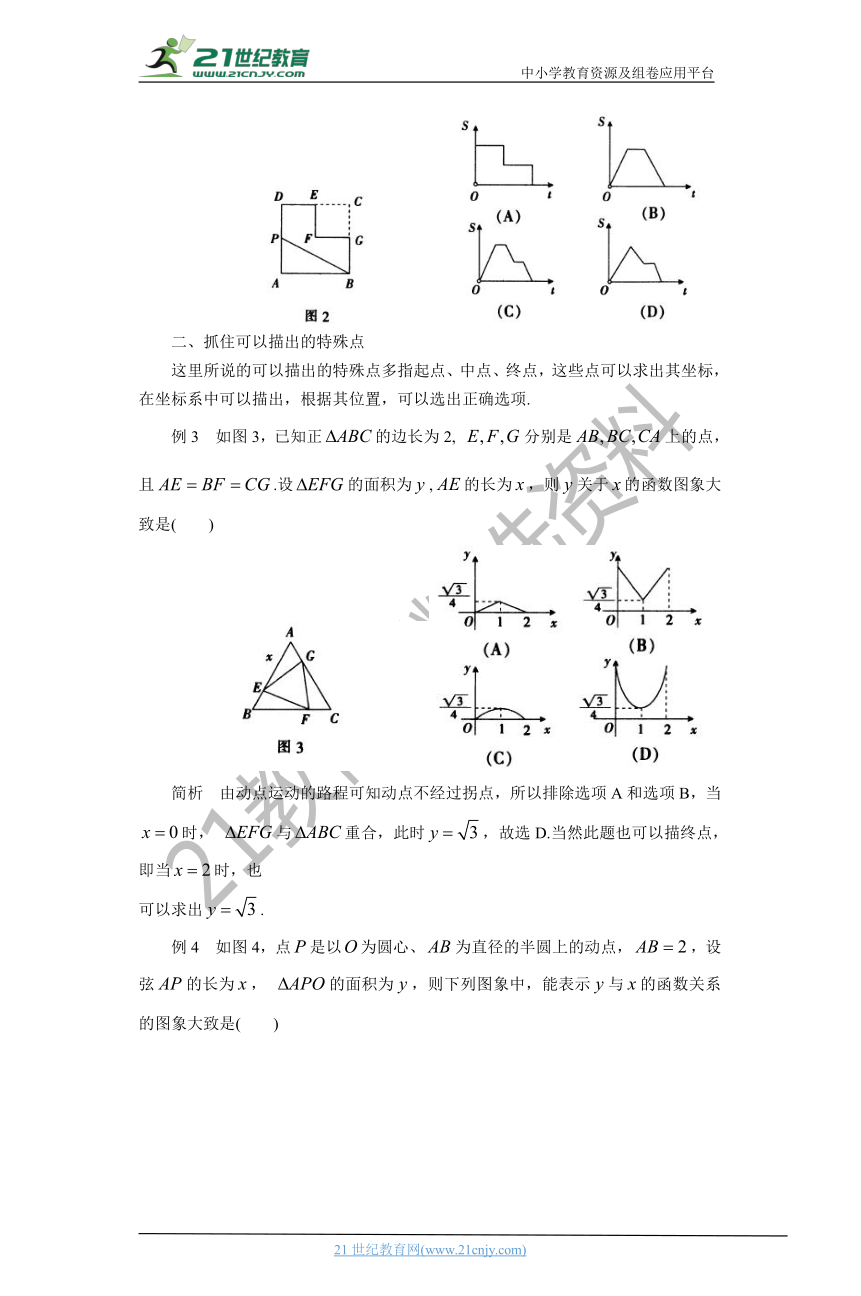
例2 如图2,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点),则的面积随着时间‘变化的函数图象大致为( )
简析 由图2可知动点运动全程一共经过四个拐点.再看选项,选项A三个拐点,选项B两个拐点,选项C四个拐点,选项D三个拐点,故选C.
二、抓住可以描出的特殊点
这里所说的可以描出的特殊点多指起点、中点、终点,这些点可以求出其坐标,在坐标系中可以描出,根据其位置,可以选出正确选项.
例3 如图3,已知正的边长为2, 分别是上的点,且.设的面积为,的长为,则关于的函数图象大致是( )
简析 由动点运动的路程可知动点不经过拐点,所以排除选项A和选项B,当时, 与重合,此时,故选D.当然此题也可以描终点,即当时,也
可以求出.
例4 如图4,点是以为圆心、为直径的半圆上的动点,,设弦的长为, 的面积为,则下列图象中,能表示与的函数关系的图象大致是( )
简析 由图4知点运动全程不经过拐点,故排除选项C和选项D,而起点和终点对于选项A和选项B是相同的,所以只能描中点,即当时,是边长为1的等边三角形,此时,点(1,0. 433)显然在选项A的图象上,故选A.当然此题也可以描出图象的最高点,即当时,可以求出,故选A.2-1-c-n-j-y
以上几例充分说明,抓住拐点和描出特殊点,可以使该类问题的解决变得轻而易举.
_21?????????è?????(www.21cnjy.com)_
解决动点生成的函数图象压轴选择题
由动点生成的函数图_è±?é??é????????è??_几年中考的热点问题.此类问题多出现在选择压轴题中,可见其分量,因此不少学生往往是望而却步.笔者通过研究发现,抓住“两点”,可以使该类问题轻松获解,下面略举几例与大家分享.
一、抓住“拐点”
这里所说的“拐点”指的是,动点经过多边形的顶点时,生成的函数图象不平滑,即出了“尖”,我们称之为“拐点”.
例1 已知点为某封闭图形边界上一定点,动点从点出发,沿其边界顺时针匀速运动一周.设点运动的时间为,线段的长为,表示与的函数关系的图象大致如图1,则该封闭图形可能是( )
简析 由_???è±????????????¨_点在整个运动过程中经过两个拐点,下面我们看选项:A选项全程有两个拐点,B选项和C选项全程都有三个拐点,D选项全程无拐点,故选A.
例2 如图2,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点),则的面积随着时间‘变化的函数图象大致为( )
简析 由图2可知动点运动全程一共经过四个拐点.再看选项,选项A三个拐点,选项B两个拐点,选项C四个拐点,选项D三个拐点,故选C.
二、抓住可以描出的特殊点
这里所说的可以描出的特殊点多指起点、中点、终点,这些点可以求出其坐标,在坐标系中可以描出,根据其位置,可以选出正确选项.
例3 如图3,已知正的边长为2, 分别是上的点,且.设的面积为,的长为,则关于的函数图象大致是( )
简析 由动点运动的路程可知动点不经过拐点,所以排除选项A和选项B,当时, 与重合,此时,故选D.当然此题也可以描终点,即当时,也
可以求出.
例4 如图4,点是以为圆心、为直径的半圆上的动点,,设弦的长为, 的面积为,则下列图象中,能表示与的函数关系的图象大致是( )
简析 由图4知点运动全程不经过拐点,故排除选项C和选项D,而起点和终点对于选项A和选项B是相同的,所以只能描中点,即当时,是边长为1的等边三角形,此时,点(1,0. 433)显然在选项A的图象上,故选A.当然此题也可以描出图象的最高点,即当时,可以求出,故选A.2-1-c-n-j-y
以上几例充分说明,抓住拐点和描出特殊点,可以使该类问题的解决变得轻而易举.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
