2021中考数学备考经典微专题 借助数学思想 求解角度问题 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 借助数学思想 求解角度问题 学案(技巧+满分解答) |
|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
借助数学思想 求解角度问题
在求解角度问题时,学生必需掌握角的平分线性质,以及角的和、差、倍、分定义及基本图形的性质,然后利用角平分线的定义、比例、方程等综合知识,以及转化、变换、分类、构造数学等思想来解决间题.以下举例说明.
一、借助“转化”求角度
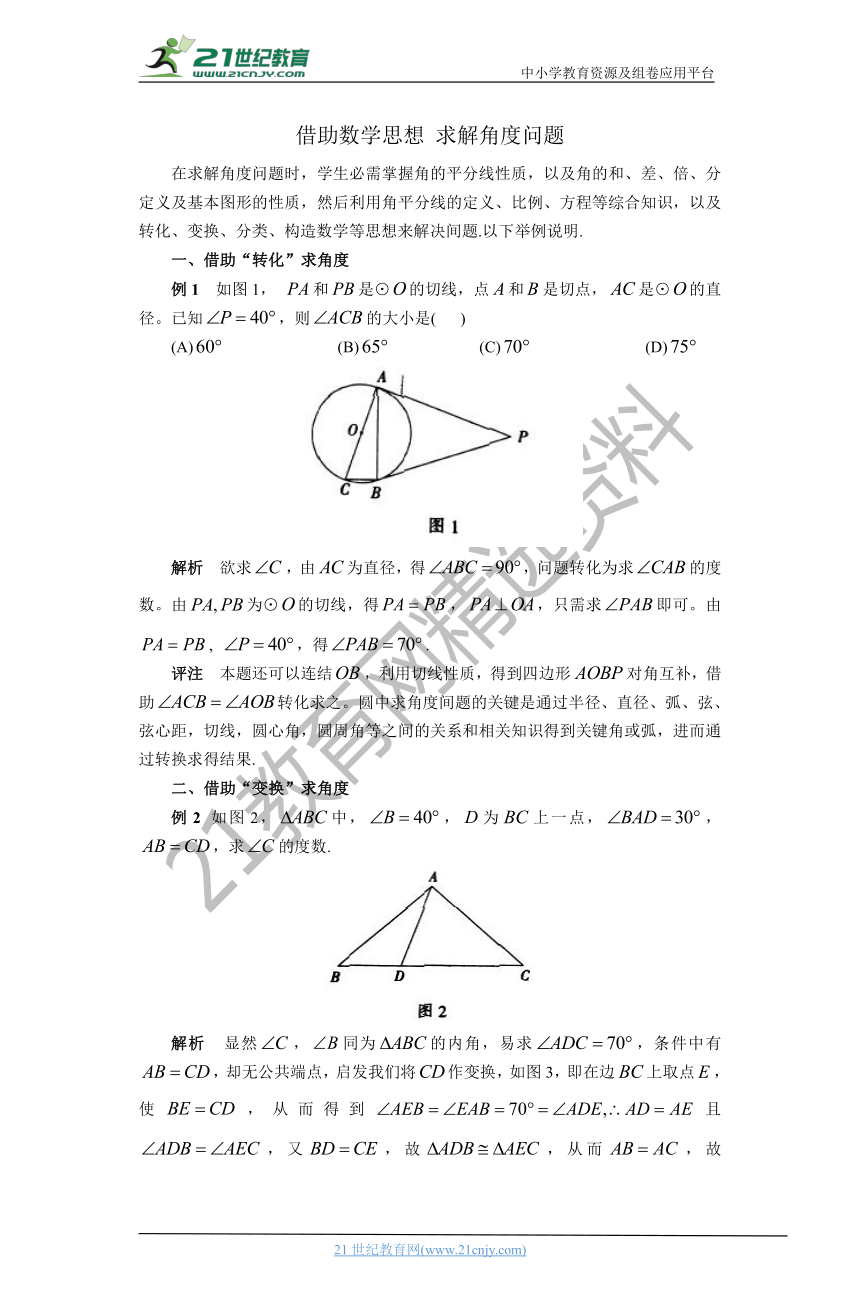
例1 如图1, 和是⊙的切线,点和是切点,是⊙的直径。已知,则的大小是( )
(A) (B) (C) (D)
解析 欲求,由为直径,得,问题转化为求的度数。由为⊙的切线,得,,只需求即可。由, ,得.
评注 本题还可以连结,利用切线性质,得到四边形对角互补,借助转化求之。圆中求角度间题的关键是通过半径、直径、弧、弦、弦心距,切线,圆心角,圆周角等之间的关系和相关知识得到关键角或弧,进而通过转换求得结果.2·1·c·n·j·y
二、借助“变换”求角度
例2 如图2,中,,为上一点,,,求的度数.
解析 显然,同为的内角,易求,条件中有,却无公共端点,启发我们将作变换,如图3,即在边上取点,使,从而得到且,又,故,从而,故.21·cn·jy·com
评注 本题的关键是借助平移这一变换让焕发活力.桥要一段一段的搭,题也是要一步一步的做,切不可妄想一步到位.搭桥不容易,解题亦艰难,都是功夫.所谓功夫,即是工夫,工夫到了,功夫也就出来了.
三、借助“构造”求角度
例3 如图4,,求的度数.
解析 由,得
.
如图4,以为底,长为腰作,连结.
由,
可得,
则,
,
所以//,。
由,得,
故。
又,故垂直平分,故。
又,
故为等边三角形,
所以,
所以,
解得,即为。
评注 本题没_????·???????è§????_,但结合已知条件构造全等三角形或相似三角形,利用有关性质及判定定理,列出方程或比例式,再用代数方法就可求得所求角的度数.www.21-cn-jy.com
四、借助“分类”求角度
例4 如图5,在中,是边的中点,求的度数.[来源:Zxxk.Com]
解析 固定,通过分析知,的大小随着和的位置而确定.和的位置有两种情况:
第一种情况,如图5,显然;
第二种情况,如图7,作,垂足为,作的垂直平分线,垂足为,交于点,连结.[来源:Zxxk.Com]【来源:21·世纪·教育·网】
则。
设,
则,
所以。
在中,
由,得。
又,从而,
所以,
所以,
又,故,
解得,
所以,.
评注 本题看似简单,却很难入手,且容易因思考不全而造成漏解。关键是“情况不明需分类.”
总之,数学思想方法是数学的灵魂,是解决数学问题的金钥匙因此,解决角的计算问题要养成善于从中考题目中挖掘更为深层的东西的习惯,寻找联系,展开拓思关健是重视提炼数学思想,学会以整体,联系,动态的观点进行思考;归纳解题方法,使零碎、隐性的解题经验显性化、系统化.只有这样,复习才会事半功倍,才能真正体现复习的价值.
_21?????????è?????(www.21cnjy.com)_
借助数学思想 求解角度问题
在求解角度问题时,学生必需掌握角的平分线性质,以及角的和、差、倍、分定义及基本图形的性质,然后利用角平分线的定义、比例、方程等综合知识,以及转化、变换、分类、构造数学等思想来解决间题.以下举例说明.
一、借助“转化”求角度
例1 如图1, 和是⊙的切线,点和是切点,是⊙的直径。已知,则的大小是( )
(A) (B) (C) (D)
解析 欲求,由为直径,得,问题转化为求的度数。由为⊙的切线,得,,只需求即可。由, ,得.
评注 本题还可以连结,利用切线性质,得到四边形对角互补,借助转化求之。圆中求角度间题的关键是通过半径、直径、弧、弦、弦心距,切线,圆心角,圆周角等之间的关系和相关知识得到关键角或弧,进而通过转换求得结果.2·1·c·n·j·y
二、借助“变换”求角度
例2 如图2,中,,为上一点,,,求的度数.
解析 显然,同为的内角,易求,条件中有,却无公共端点,启发我们将作变换,如图3,即在边上取点,使,从而得到且,又,故,从而,故.21·cn·jy·com
评注 本题的关键是借助平移这一变换让焕发活力.桥要一段一段的搭,题也是要一步一步的做,切不可妄想一步到位.搭桥不容易,解题亦艰难,都是功夫.所谓功夫,即是工夫,工夫到了,功夫也就出来了.
三、借助“构造”求角度
例3 如图4,,求的度数.
解析 由,得
.
如图4,以为底,长为腰作,连结.
由,
可得,
则,
,
所以//,。
由,得,
故。
又,故垂直平分,故。
又,
故为等边三角形,
所以,
所以,
解得,即为。
评注 本题没_????·???????è§????_,但结合已知条件构造全等三角形或相似三角形,利用有关性质及判定定理,列出方程或比例式,再用代数方法就可求得所求角的度数.www.21-cn-jy.com
四、借助“分类”求角度
例4 如图5,在中,是边的中点,求的度数.[来源:Zxxk.Com]
解析 固定,通过分析知,的大小随着和的位置而确定.和的位置有两种情况:
第一种情况,如图5,显然;
第二种情况,如图7,作,垂足为,作的垂直平分线,垂足为,交于点,连结.[来源:Zxxk.Com]【来源:21·世纪·教育·网】
则。
设,
则,
所以。
在中,
由,得。
又,从而,
所以,
所以,
又,故,
解得,
所以,.
评注 本题看似简单,却很难入手,且容易因思考不全而造成漏解。关键是“情况不明需分类.”
总之,数学思想方法是数学的灵魂,是解决数学问题的金钥匙因此,解决角的计算问题要养成善于从中考题目中挖掘更为深层的东西的习惯,寻找联系,展开拓思关健是重视提炼数学思想,学会以整体,联系,动态的观点进行思考;归纳解题方法,使零碎、隐性的解题经验显性化、系统化.只有这样,复习才会事半功倍,才能真正体现复习的价值.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
