2021中考数学备考经典微专题 例析追击和相遇问题的解题方法 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 例析追击和相遇问题的解题方法 学案(技巧+满分解答) | 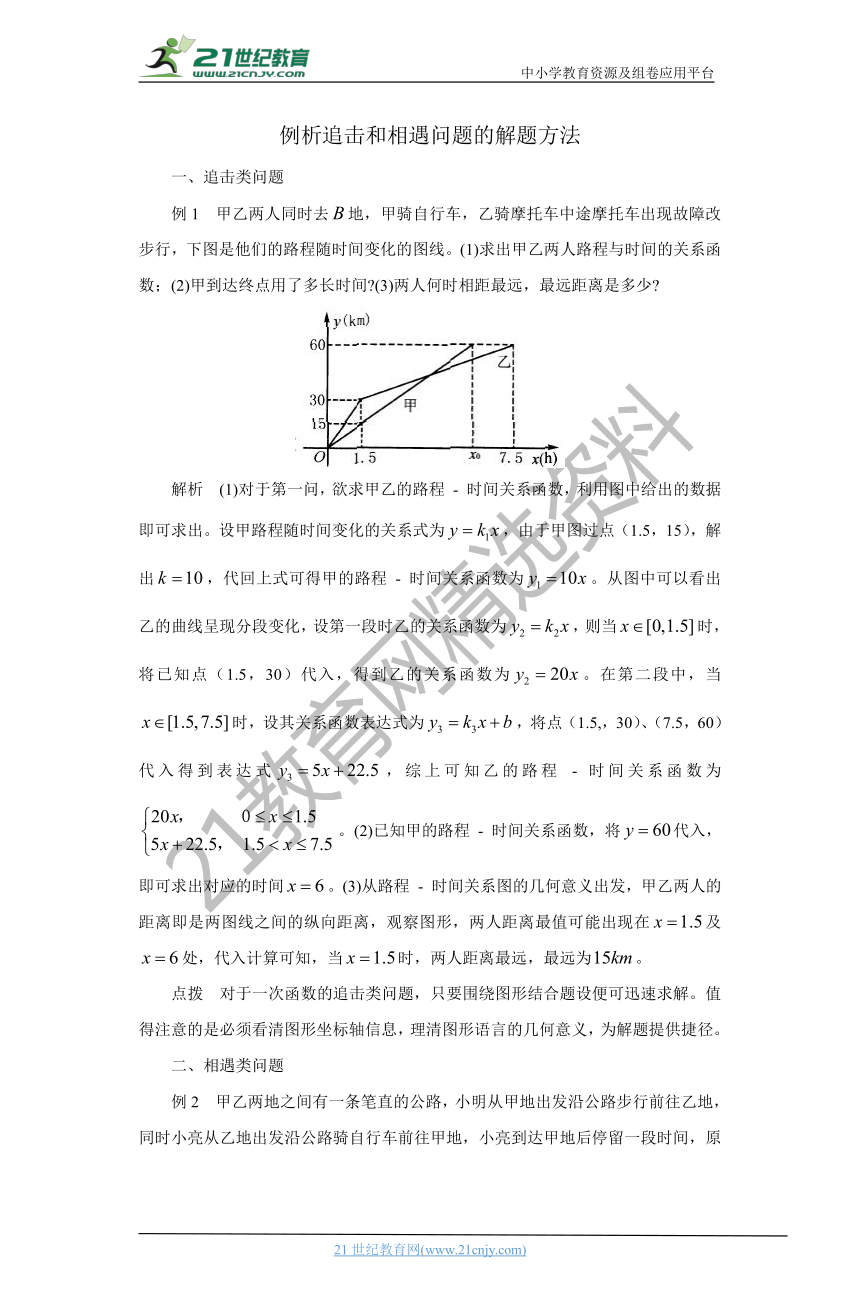 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 10:52:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
例析追击和相遇问题的解题方法
一、追击类问题
例1 甲乙两人同时去地,甲骑自行车,乙骑摩托车中途摩托车出现故障改步行,下图是他们的路程随时间变化的图线。(1)求出甲乙两人路程与时间的关系函数;(2)甲到达终点用了多长时间?(3)两人何时相距最远,最远距离是多少?
解析 (1)对于第一问,欲求甲乙的路程 - 时间关系函数,利用图中给出的数据即可求出。设甲路程随时间变化的关系式为,由于甲图过点(1.5,15),解出,代回上式可得甲的路程 - 时间关系函数为。从图中可以看出乙的曲线呈现分段变化,设第一段时乙的关系函数为,则当时,将已知点(1.5,30)代入,得到乙的关系函数为。在第二段中,当时,设其关系函数表达式为,将点(1.5,,30)、(7.5,60)代入得到表达式,综上可知乙的路程 - 时间关系函数为。(2)已知甲的路程 - 时间关系函数,将代入,即可求出对应的时间。(3)从路程 - 时间关系图的几何意义出发,甲乙两人的距离即是两图线之间的纵向距离,观察图形,两人距离最值可能出现在及处,代入计算可知,当时,两人距离最远,最远为。
点拨 对于一次函数的追击类问题,只要围绕图形结合题设便可迅速求解。值得注意的是必须看清图形坐标轴信息,理清图形语言的几何意义,为解题提供捷径。
二、相遇类问题
例2 甲乙两地之间有一条笔直的公路,小明从甲地出发沿公路步行前往乙地,同时小亮从乙地出发沿公路骑自行车前往甲地,小亮到达甲地后停留一段时间,原路原速返回,追上小明后两人一起步行到乙地。设小明与甲地的距离为,小亮与甲地的距离为,小明小亮之间的距离为,小明行走时间为,与之间的函数图象如图1,与之间的部分图形如图2。(1)求小亮从乙到甲的与之间的函数关系;(2)求小亮由甲返回到与小明相遇的与的函数关系;(3)补全图2的信息,并求出值。
解析 图1是小明与小亮的路程 - 时间图象,结合题目背景可知,段是小亮从乙地到甲地的过程,设其关系式为,将已知点代人可得、,得到其关系式为。
(2)段为小亮在甲地停留的过程,段则是小亮与小明相遇的过程,设,已知小亮的骑行速度,结合已知点,可得段的关系式为,同时可以得到。此时,小亮与小明相遇的与的关系即是与之间的纵坐标之差,。
(3)首先,a值表示两人第一次相遇时间,已知两地距离与两人速度,。段::当时,小亮到达甲地,此后14分钟,小亮停留在甲地,此时,两人之间的距离满足关系:。段:此时,小亮出发往乙地,直至与小明相遇,两人之间的距离。满足关系式,最终状态两人相遇即,此段的时间。段:此时两人已经相遇,且同时步行至乙地,故两人之间的距离始终为0。至此,对两人的运动过程的分析全部完成,将对应的关系式与区间段代入图形即可得到对应的图2。
点拨 遇到复杂类型的相遇追击问题,切忌慌乱,此时可以多读题目,将题目背景与图形进行反复关联对照。同时,将已知的信息尽可能多的标注在图形上,从而提高审题效率。
一次函数类的相遇与追击问题常常与学生的生活实际相联系,有条件时我们不妨安排学生进行模拟实验,在生动趣味的实验过程中深化学生理解。在教学过程中,尽可能追求学生对题目图形的理解,务必做到图形与情境的一一对应。
_21?????????è?????(www.21cnjy.com)_
例析追击和相遇问题的解题方法
一、追击类问题
例1 甲乙两人同时去地,甲骑自行车,乙骑摩托车中途摩托车出现故障改步行,下图是他们的路程随时间变化的图线。(1)求出甲乙两人路程与时间的关系函数;(2)甲到达终点用了多长时间?(3)两人何时相距最远,最远距离是多少?
解析 (1)对于第一问,欲求甲乙的路程 - 时间关系函数,利用图中给出的数据即可求出。设甲路程随时间变化的关系式为,由于甲图过点(1.5,15),解出,代回上式可得甲的路程 - 时间关系函数为。从图中可以看出乙的曲线呈现分段变化,设第一段时乙的关系函数为,则当时,将已知点(1.5,30)代入,得到乙的关系函数为。在第二段中,当时,设其关系函数表达式为,将点(1.5,,30)、(7.5,60)代入得到表达式,综上可知乙的路程 - 时间关系函数为。(2)已知甲的路程 - 时间关系函数,将代入,即可求出对应的时间。(3)从路程 - 时间关系图的几何意义出发,甲乙两人的距离即是两图线之间的纵向距离,观察图形,两人距离最值可能出现在及处,代入计算可知,当时,两人距离最远,最远为。
点拨 对于一次函数的追击类问题,只要围绕图形结合题设便可迅速求解。值得注意的是必须看清图形坐标轴信息,理清图形语言的几何意义,为解题提供捷径。
二、相遇类问题
例2 甲乙两地之间有一条笔直的公路,小明从甲地出发沿公路步行前往乙地,同时小亮从乙地出发沿公路骑自行车前往甲地,小亮到达甲地后停留一段时间,原路原速返回,追上小明后两人一起步行到乙地。设小明与甲地的距离为,小亮与甲地的距离为,小明小亮之间的距离为,小明行走时间为,与之间的函数图象如图1,与之间的部分图形如图2。(1)求小亮从乙到甲的与之间的函数关系;(2)求小亮由甲返回到与小明相遇的与的函数关系;(3)补全图2的信息,并求出值。
解析 图1是小明与小亮的路程 - 时间图象,结合题目背景可知,段是小亮从乙地到甲地的过程,设其关系式为,将已知点代人可得、,得到其关系式为。
(2)段为小亮在甲地停留的过程,段则是小亮与小明相遇的过程,设,已知小亮的骑行速度,结合已知点,可得段的关系式为,同时可以得到。此时,小亮与小明相遇的与的关系即是与之间的纵坐标之差,。
(3)首先,a值表示两人第一次相遇时间,已知两地距离与两人速度,。段::当时,小亮到达甲地,此后14分钟,小亮停留在甲地,此时,两人之间的距离满足关系:。段:此时,小亮出发往乙地,直至与小明相遇,两人之间的距离。满足关系式,最终状态两人相遇即,此段的时间。段:此时两人已经相遇,且同时步行至乙地,故两人之间的距离始终为0。至此,对两人的运动过程的分析全部完成,将对应的关系式与区间段代入图形即可得到对应的图2。
点拨 遇到复杂类型的相遇追击问题,切忌慌乱,此时可以多读题目,将题目背景与图形进行反复关联对照。同时,将已知的信息尽可能多的标注在图形上,从而提高审题效率。
一次函数类的相遇与追击问题常常与学生的生活实际相联系,有条件时我们不妨安排学生进行模拟实验,在生动趣味的实验过程中深化学生理解。在教学过程中,尽可能追求学生对题目图形的理解,务必做到图形与情境的一一对应。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
