2021中考数学备考经典微专题 一个数形结合模型及其在解题中的运用 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 一个数形结合模型及其在解题中的运用 学案(技巧+满分解答) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
一个数形结合模型及其在解题中的运用
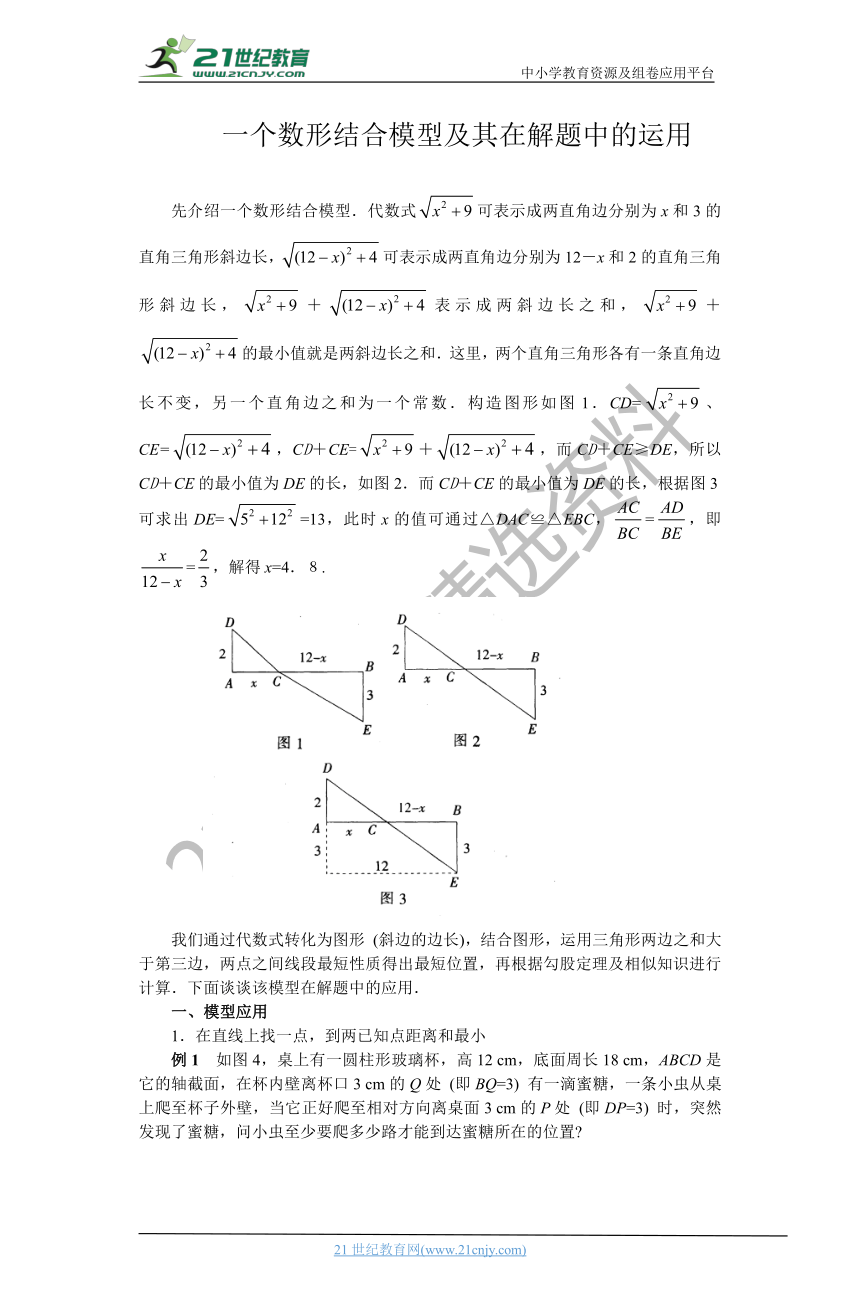
先介绍一个数形结合模型.代数式可表示成两直角边分别为x和3的直角三角形斜边长,可表示成两直角边分别为12-x和2的直角三角形斜边长,+表示成两斜边长之和,+的最小值就是两斜边长之和.这里,两个直角三角形各有一条直角边长不变,另一个直角边之和为一个常数.构造图形如图1.CD=、CE=,CD+CE=+,而CD+CE≥DE,所以CD+CE的最小值为DE的长,如图2.而CD+CE的最小值为DE的长,根据图3可求出DE==13,此时x的值可通过△DAC≌△EBC,=,即=,解得x=4.8.
我们通过代数式转化为_??????_(???è??_的边长),结合图形,运用三角形两边之和大于第三边,两点之间线段最短性质得出最短位置,再根据勾股定理及相似知识进行计算.下面谈谈该模型在解题中的应用.
一、模型应用
1.在直线上找一点,到两已知点距离和最小
例1 __??????4??????_上有一圆柱形玻璃杯,高12 cm,底面周长18 cm,ABCD是它的轴截面,在杯内壁离杯口3 cm的Q处 (即BQ=3) 有一滴蜜糖,一条小虫从桌上爬至杯子外壁,当它正好爬至相对方向离桌面3 cm的P处 (即DP=3) 时,突然发现了蜜糖,问小虫至少要爬多少路才能到达蜜糖所在的位置?
分析 把圆柱侧面展开,_?????????????¤????_小虫在外壁P,一定要通过杯口即展开图中线段BC上一点H到内壁Q,要求PH+HQ的最小值.按照上述模型解题思路,第一步求出PH、HQ的代数式,第二步画出对应图形,第三步根据图形运用勾股定理知识解决.21·cn·jy·com
解 设CH=a,∵ BC=9,∴ BH=9-a;又BQ=3,CP=9.
∴ PH= ,
HQ=
∴ P H+H Q=+.
根据代数式构造图形如图5.
PH+HQ的最小值为
PQ==15.
2.在一条直线上找一定长线段,使它两端分别到两已知点距离和最小
例2 如图6,在平_é?????è§??????????_中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.
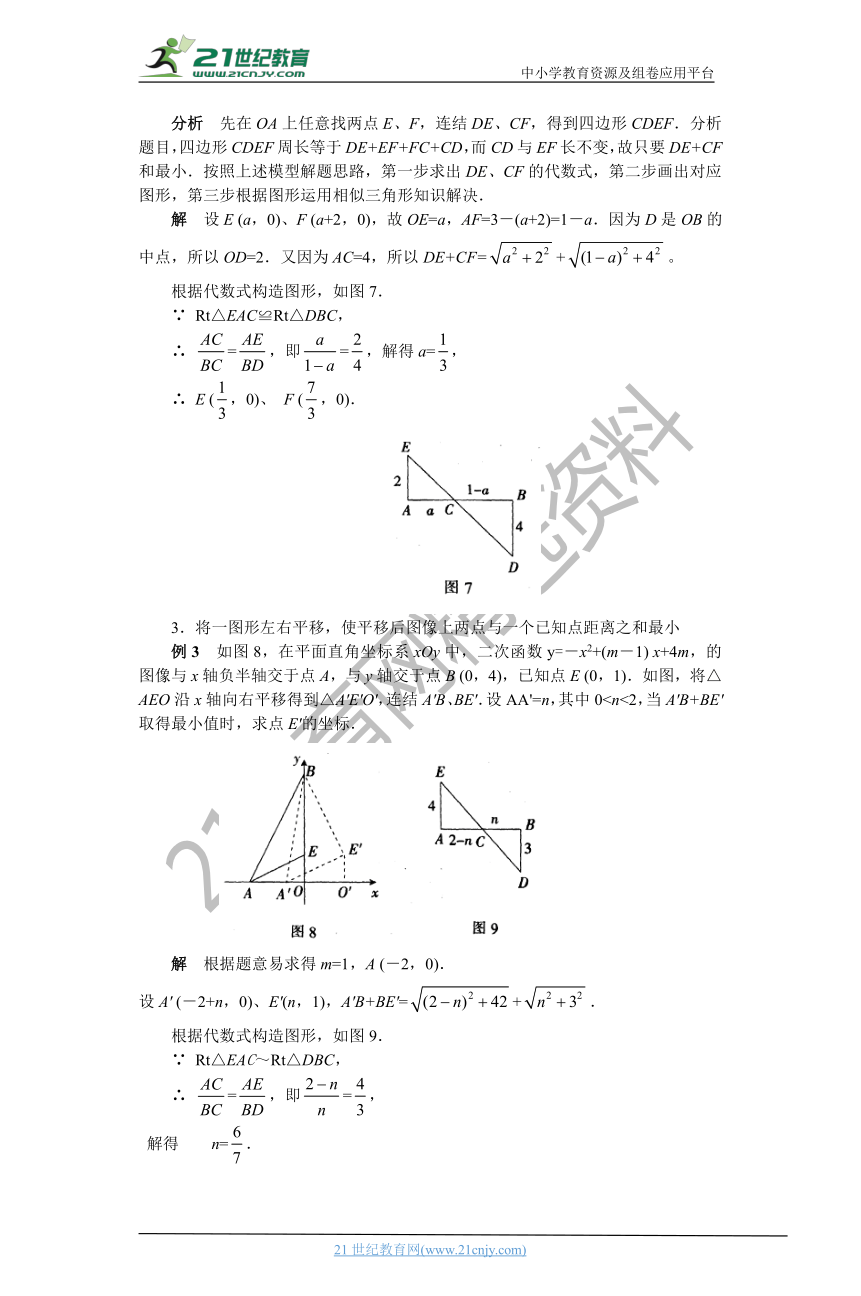
分析 先在OA上任意找_??¤???E???F???_连结DE、CF,得到四边形CDEF.分析题目,四边形CDEF周长等于DE+EF+FC+CD,而CD与EF长不变,故只要DE+CF和最小.按照上述模型解题思路,第一步求出DE、CF的代数式,第二步画出对应图形,第三步根据图形运用相似三角形知识解决.
解 设E (a,0)、F (a+2,0),故OE=a,AF=3-(a+2)=1-a.因为D是OB的中点,所以OD=2.又因为AC=4,所以DE+CF=+。
根据代数式构造图形,如图7.
∵ Rt△EAC≌Rt△DBC,
∴ =,即=,解得a=,
∴ E (,0)、 F (,0).
3.将一图形左右平移,使平移后图像上两点与一个已知点距离之和最小
例3 __??????8?????¨_平面直角坐标系xOy中,二次函数y=-x2+(m-1) x+4m,的图像与x轴负半轴交于点A,与y轴交于点B (0,4),已知点E (0,1).如图,将△AEO沿x轴向右平移得到△A'E'O',连结A'B、BE'.设AA'=n,其中0 解 根据题意易求得m=1,A (-2,0).
设A' (-2+n,0)、E'(n,1),A'B+BE'=+.
根据代数式构造图形,如图9.
∵ Rt△EAC~Rt△DBC,
∴ =,即=,
解得 n=.
∴ E' (,1).
4.将一图形左右平移,使平移后图像上两点分别与两个已知点距离之和最小
例4 如图10,直_???y=2x+_6上有两点A (-3.5,n)、B (-1,m),y轴上有两点C (0,2)、D (0,3),现将直线y=2x+6左右平移,点A平移后对应点记作A',点B平移后对应点记作B',若A'C+B'D最小,求平移后的直线解析式.
解 易求出n=1,m=4.设直线向右平移a个单位,A' (-3.5+ a,1)、B' (-1+ a,4),A'C+B'D =+.
因为3.5-a与l-a的和不是一个常数,而(1-a)2=(a-1)2,故A'C+B'D=+.
根据代数式构造图形,如图11.
∵ Rt△EAC~Rt△DBC,
∴ =,即=,解得a=2.25,∴ 需要将直线向右平移2.25个单位,平移后的直线为y=2(x-2.25)+6,即y=2x+1.5.
5.综合应用
例5 如图12,已知点A (-4,8) 和B (2,n) 在抛物线y=ax2上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标.
(2) 平移抛_??????y=ax_2,记平移后点A的对应点为A',点B的对应点为B',点C (-2,0) 和点D (-4,0) 是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A'C+CB' 最短,求此时抛物线的函数解析式;
② 当抛物线向左或_??????????§???????_是否存在某个位置,使四边形A'B'CD的周长最短? 若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
分析 这道题目3个问题都是求两线段
和最小,分别属_????¨?????????¨1_、3、4,只需按照模型解题思路,第一步求出对应两线段代数式,第二步根据对应代数式画出相应图形,第三步根据图形运用勾股定理或相似知识进行计算.
解 (1) 易求a=,B关于x轴对称点P (2,-2),抛物线为y=x2.
设Q (a,0),
AQ+BQ=+.
根据代数式构造图形,如图13.
∵ Rt△EAC~Rt△DBC,
∴ =,即=,
解得 a=,∴Q (,0).
(2) 设抛物线向左平移a个单位,如图14,则 A' (-4-a,8)、B' (2-a,2),A'C+CB'=+.
根据代数式构造图形,如图15.
∵ Rt△EAC∽Rt△DBC,
∴ =,即=,解得a=,
∴ 抛物线y=x2向左平移个单位后解析式为y=+(x+)2
(3) 设抛物_???????·?????§?a_个单位,如图16.则A' (-4-a,8)、B' (2-a,2).因为CD、A'B'长度已知,四边形A'B'CD周长最小实质就是A'D+B'C最小.
A'D+CB' =+,
根据代数式构造图形,如图17.
∵ R t△EAC~R t△DBC
∴ =,即=,解得a=,
∴ 抛物线y=x2向左平移个单位后解析式为y=(x+)2.
回顾模型在上述_???é?????????????¨_,都是先将两线段长用代数式表示出来,然后根据得到的代数式画出对应图形,再结合图形,运用相关数学知识进行计算.它用一种解题模式解决了众多变化多端的数学题,做到以不变应万变,在教学中深受学生喜爱.
_21?????????è?????(www.21cnjy.com)_
一个数形结合模型及其在解题中的运用
先介绍一个数形结合模型.代数式可表示成两直角边分别为x和3的直角三角形斜边长,可表示成两直角边分别为12-x和2的直角三角形斜边长,+表示成两斜边长之和,+的最小值就是两斜边长之和.这里,两个直角三角形各有一条直角边长不变,另一个直角边之和为一个常数.构造图形如图1.CD=、CE=,CD+CE=+,而CD+CE≥DE,所以CD+CE的最小值为DE的长,如图2.而CD+CE的最小值为DE的长,根据图3可求出DE==13,此时x的值可通过△DAC≌△EBC,=,即=,解得x=4.8.
我们通过代数式转化为_??????_(???è??_的边长),结合图形,运用三角形两边之和大于第三边,两点之间线段最短性质得出最短位置,再根据勾股定理及相似知识进行计算.下面谈谈该模型在解题中的应用.
一、模型应用
1.在直线上找一点,到两已知点距离和最小
例1 __??????4??????_上有一圆柱形玻璃杯,高12 cm,底面周长18 cm,ABCD是它的轴截面,在杯内壁离杯口3 cm的Q处 (即BQ=3) 有一滴蜜糖,一条小虫从桌上爬至杯子外壁,当它正好爬至相对方向离桌面3 cm的P处 (即DP=3) 时,突然发现了蜜糖,问小虫至少要爬多少路才能到达蜜糖所在的位置?
分析 把圆柱侧面展开,_?????????????¤????_小虫在外壁P,一定要通过杯口即展开图中线段BC上一点H到内壁Q,要求PH+HQ的最小值.按照上述模型解题思路,第一步求出PH、HQ的代数式,第二步画出对应图形,第三步根据图形运用勾股定理知识解决.21·cn·jy·com
解 设CH=a,∵ BC=9,∴ BH=9-a;又BQ=3,CP=9.
∴ PH= ,
HQ=
∴ P H+H Q=+.
根据代数式构造图形如图5.
PH+HQ的最小值为
PQ==15.
2.在一条直线上找一定长线段,使它两端分别到两已知点距离和最小
例2 如图6,在平_é?????è§??????????_中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.
分析 先在OA上任意找_??¤???E???F???_连结DE、CF,得到四边形CDEF.分析题目,四边形CDEF周长等于DE+EF+FC+CD,而CD与EF长不变,故只要DE+CF和最小.按照上述模型解题思路,第一步求出DE、CF的代数式,第二步画出对应图形,第三步根据图形运用相似三角形知识解决.
解 设E (a,0)、F (a+2,0),故OE=a,AF=3-(a+2)=1-a.因为D是OB的中点,所以OD=2.又因为AC=4,所以DE+CF=+。
根据代数式构造图形,如图7.
∵ Rt△EAC≌Rt△DBC,
∴ =,即=,解得a=,
∴ E (,0)、 F (,0).
3.将一图形左右平移,使平移后图像上两点与一个已知点距离之和最小
例3 __??????8?????¨_平面直角坐标系xOy中,二次函数y=-x2+(m-1) x+4m,的图像与x轴负半轴交于点A,与y轴交于点B (0,4),已知点E (0,1).如图,将△AEO沿x轴向右平移得到△A'E'O',连结A'B、BE'.设AA'=n,其中0
设A' (-2+n,0)、E'(n,1),A'B+BE'=+.
根据代数式构造图形,如图9.
∵ Rt△EAC~Rt△DBC,
∴ =,即=,
解得 n=.
∴ E' (,1).
4.将一图形左右平移,使平移后图像上两点分别与两个已知点距离之和最小
例4 如图10,直_???y=2x+_6上有两点A (-3.5,n)、B (-1,m),y轴上有两点C (0,2)、D (0,3),现将直线y=2x+6左右平移,点A平移后对应点记作A',点B平移后对应点记作B',若A'C+B'D最小,求平移后的直线解析式.
解 易求出n=1,m=4.设直线向右平移a个单位,A' (-3.5+ a,1)、B' (-1+ a,4),A'C+B'D =+.
因为3.5-a与l-a的和不是一个常数,而(1-a)2=(a-1)2,故A'C+B'D=+.
根据代数式构造图形,如图11.
∵ Rt△EAC~Rt△DBC,
∴ =,即=,解得a=2.25,∴ 需要将直线向右平移2.25个单位,平移后的直线为y=2(x-2.25)+6,即y=2x+1.5.
5.综合应用
例5 如图12,已知点A (-4,8) 和B (2,n) 在抛物线y=ax2上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标.
(2) 平移抛_??????y=ax_2,记平移后点A的对应点为A',点B的对应点为B',点C (-2,0) 和点D (-4,0) 是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A'C+CB' 最短,求此时抛物线的函数解析式;
② 当抛物线向左或_??????????§???????_是否存在某个位置,使四边形A'B'CD的周长最短? 若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
分析 这道题目3个问题都是求两线段
和最小,分别属_????¨?????????¨1_、3、4,只需按照模型解题思路,第一步求出对应两线段代数式,第二步根据对应代数式画出相应图形,第三步根据图形运用勾股定理或相似知识进行计算.
解 (1) 易求a=,B关于x轴对称点P (2,-2),抛物线为y=x2.
设Q (a,0),
AQ+BQ=+.
根据代数式构造图形,如图13.
∵ Rt△EAC~Rt△DBC,
∴ =,即=,
解得 a=,∴Q (,0).
(2) 设抛物线向左平移a个单位,如图14,则 A' (-4-a,8)、B' (2-a,2),A'C+CB'=+.
根据代数式构造图形,如图15.
∵ Rt△EAC∽Rt△DBC,
∴ =,即=,解得a=,
∴ 抛物线y=x2向左平移个单位后解析式为y=+(x+)2
(3) 设抛物_???????·?????§?a_个单位,如图16.则A' (-4-a,8)、B' (2-a,2).因为CD、A'B'长度已知,四边形A'B'CD周长最小实质就是A'D+B'C最小.
A'D+CB' =+,
根据代数式构造图形,如图17.
∵ R t△EAC~R t△DBC
∴ =,即=,解得a=,
∴ 抛物线y=x2向左平移个单位后解析式为y=(x+)2.
回顾模型在上述_???é?????????????¨_,都是先将两线段长用代数式表示出来,然后根据得到的代数式画出对应图形,再结合图形,运用相关数学知识进行计算.它用一种解题模式解决了众多变化多端的数学题,做到以不变应万变,在教学中深受学生喜爱.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
