2021中考数学备考经典微专题 由圆的定义发现隐圆巧解实际问题 学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 由圆的定义发现隐圆巧解实际问题 学案(技巧+满分解答) | 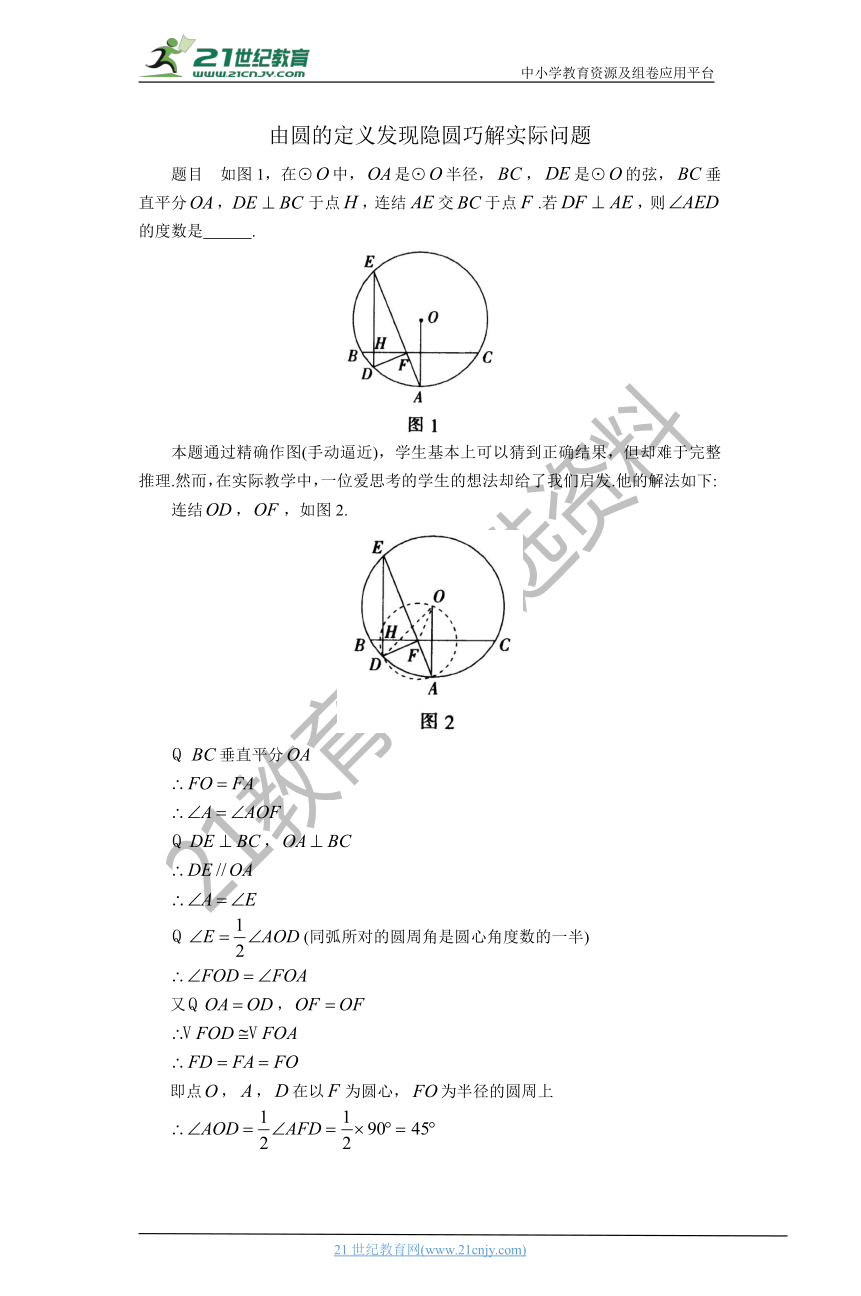 | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 11:58:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
由圆的定义发现隐圆巧解实际问题
题目 如图1,在⊙中,是⊙半径,,是⊙的弦,垂直平分,于点,连结交于点.若,则的度数是 .
[来源:学科网]
本题通过精确作图(手动逼近),学生基本上可以猜到正确结果,但却难于完整推理.然而,在实际教学中,一位爱思考的学生的想法却给了我们启发.他的解法如下:[来
连结,,如图2.
垂直平分
,
(同弧所对的圆周角是圆心角度数的一半)
又,
即点,,在以为圆心,为半径的圆周上
题1
已知:是半径为1的⊙的一条弦,且,以为一边在⊙内作正,为⊙上不同于点的一点,且,的延长线交⊙于点,则的长为( )
(A) (B) (C) (D)
解 如图3,连结,以为圆心,长为半径作圆.
,,都在⊙上
而在⊙中,弧的度数等于的度数,其大小为,
,选B.
题2
如图4,,于点,交于点.
求证:的面积
证明
点,,在⊙上(如图5).
,
,
又
又
总结对于圆的问题,往往可以通过弧(同弧或等弧)实现角的转换.因此,添作辅助圆,把角放入同圆中,利用同弧所对的圆周角与圆心角的数量关系,就可以进行灵活转换,达到简化计算或证明的目的.这里,发现共圆是关键,而根据圆的定义找圆是一条有效的途径,但在实际解题中,往往被我们很多人忽略了.因此,建议同学们做个有心人,解题时不要忘了作为根基的圆的定义,也许它会给你意外的惊喜.
_21?????????è?????(www.21cnjy.com)_
由圆的定义发现隐圆巧解实际问题
题目 如图1,在⊙中,是⊙半径,,是⊙的弦,垂直平分,于点,连结交于点.若,则的度数是 .
[来源:学科网]
本题通过精确作图(手动逼近),学生基本上可以猜到正确结果,但却难于完整推理.然而,在实际教学中,一位爱思考的学生的想法却给了我们启发.他的解法如下:[来
连结,,如图2.
垂直平分
,
(同弧所对的圆周角是圆心角度数的一半)
又,
即点,,在以为圆心,为半径的圆周上
题1
已知:是半径为1的⊙的一条弦,且,以为一边在⊙内作正,为⊙上不同于点的一点,且,的延长线交⊙于点,则的长为( )
(A) (B) (C) (D)
解 如图3,连结,以为圆心,长为半径作圆.
,,都在⊙上
而在⊙中,弧的度数等于的度数,其大小为,
,选B.
题2
如图4,,于点,交于点.
求证:的面积
证明
点,,在⊙上(如图5).
,
,
又
又
总结对于圆的问题,往往可以通过弧(同弧或等弧)实现角的转换.因此,添作辅助圆,把角放入同圆中,利用同弧所对的圆周角与圆心角的数量关系,就可以进行灵活转换,达到简化计算或证明的目的.这里,发现共圆是关键,而根据圆的定义找圆是一条有效的途径,但在实际解题中,往往被我们很多人忽略了.因此,建议同学们做个有心人,解题时不要忘了作为根基的圆的定义,也许它会给你意外的惊喜.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
