2021中考数学备考经典微专题 “正六边形”考点透析学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 “正六边形”考点透析学案(技巧+满分解答) | 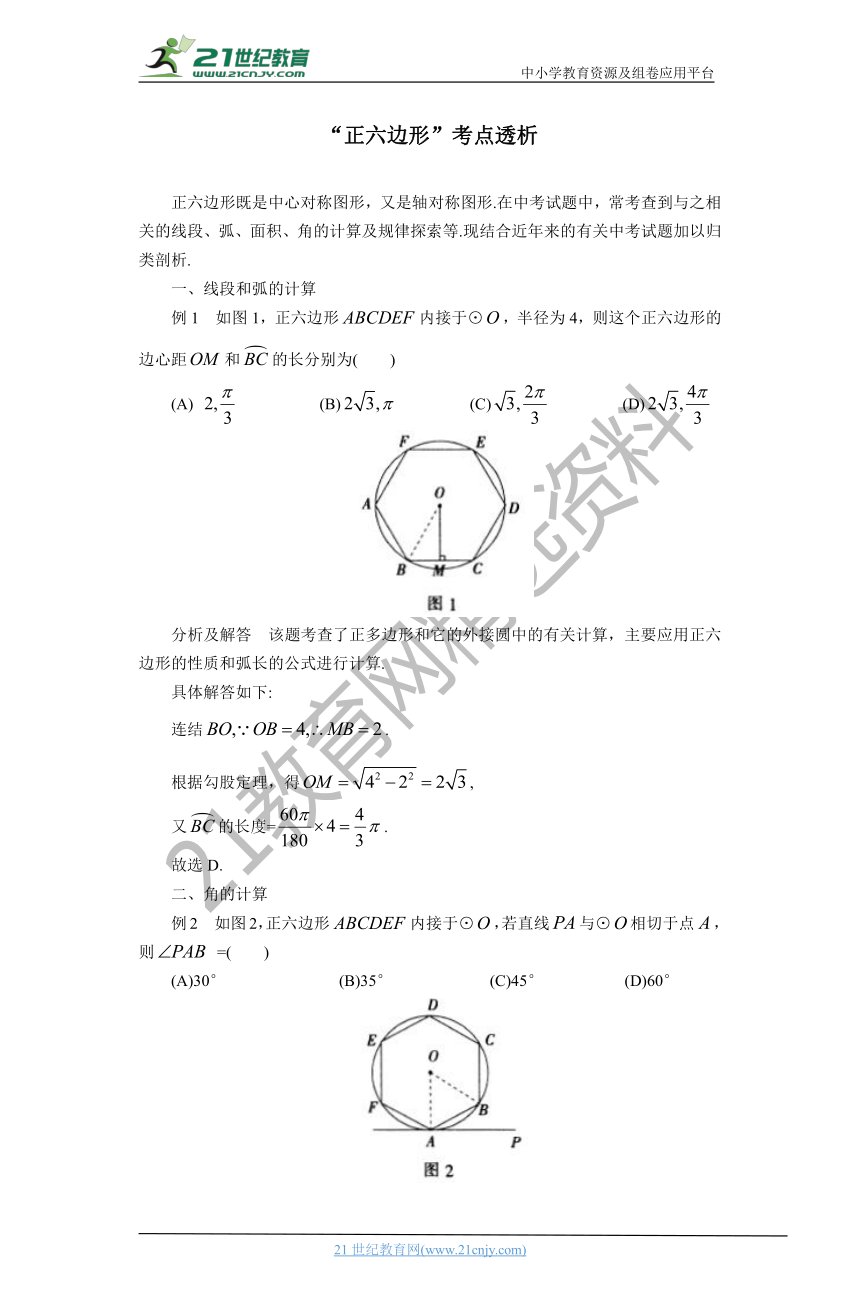 | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 12:04:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
“正六边形”考点透析
正六边形既是中_???????§°?????????_又是轴对称图形.在中考试题中,常考查到与之相关的线段、弧、面积、角的计算及规律探索等.现结合近年来的有关中考试题加以归类剖析.21·cn·jy·com
一、线段和弧的计算
例1 如图1,正六边形内接于⊙,半径为4,则这个正六边形的边心距和的长分别为( )www.21-cn-jy.com
(A) (B) (C) (D)
分析及解答 该题考查了正多边形和它的外接圆中的有关计算,主要应用正六边形的性质和弧长的公式进行计算.
具体解答如下:
连结.
根据勾股定理,得,
又的长度=.
故选D.
二、角的计算
例2 如图2,正六边形内接于⊙,若直线与⊙相切于点,则 =( )
(A)30° (B)35° (C)45° (D)60°
分析及解答 该题的解决主要是利用切线和正六边形的性质.具体解答如下:
连结,则是等边三角形,
.
又是⊙的切线,
,
.
故选A.
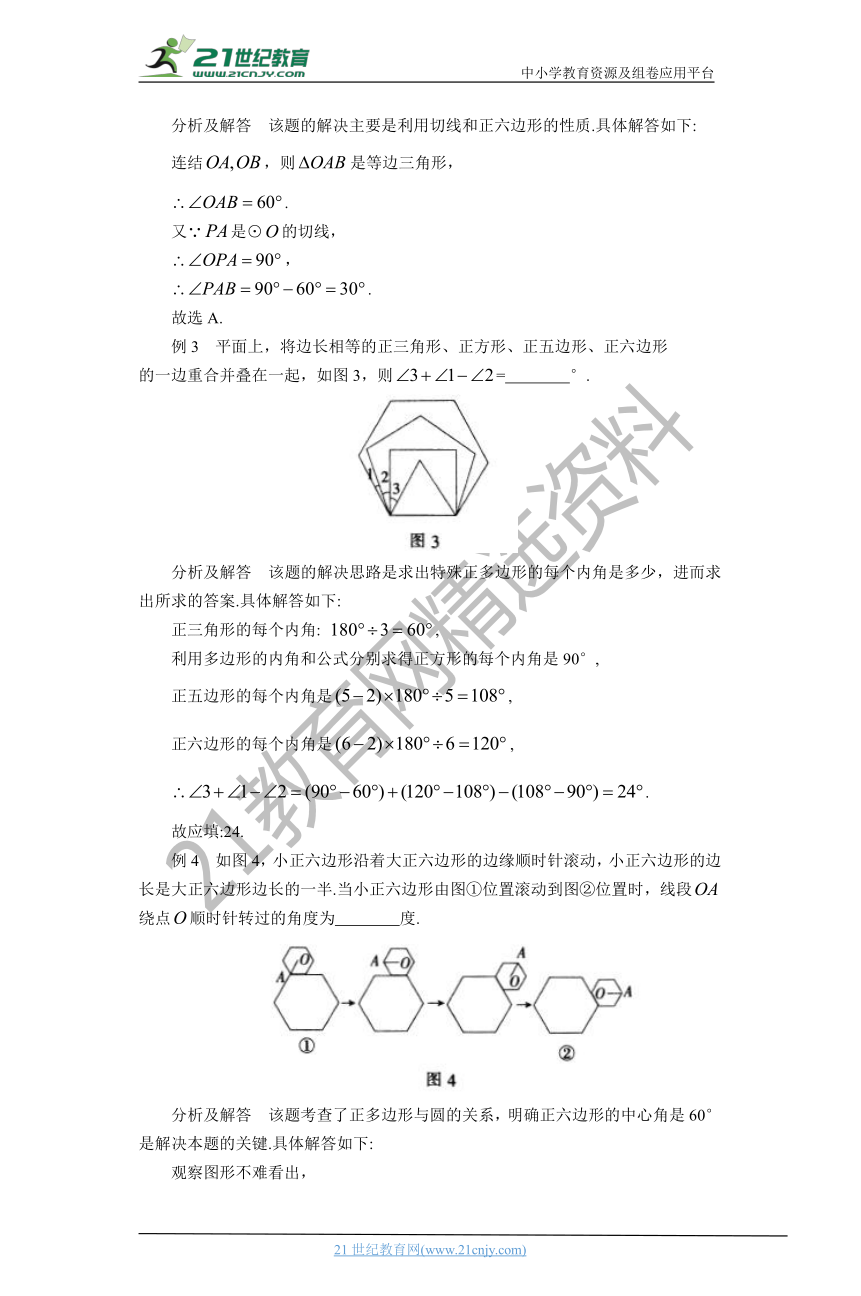
例3 平面上,将边长相等的正三角形、正方形、正五边形、正六边形
的一边重合并叠在一起,如图3,则= °.
分析及解答 该题的解决思路是求出特殊正多边形的每个内角是多少,进而求出所求的答案.具体解答如下:
正三角形的每个内角: ,
利用多边形的内角和公式分别求得正方形的每个内角是90°,
正五边形的每个内角是,
正六边形的每个内角是,
.
故应填:24.
例4 如图4,小正六边形沿着大正六边形的边缘顺时针滚动,小正六边形的边长是大正六边形边长的一半.当小正六边形由图①位置滚动到图②位置时,线段绕点顺时针转过的角度为 度.2·1·c·n·j·y
分析及解答 该题考查了正多边形与圆的关系,明确正六边形的中心角是60°是解决本题的关键.具体解答如下:
观察图形不难看出,
第一个到第二个转过了60°;
第二个到第三个转过了120°;
第三个到第四个又转过了60°,所以总共转动了240 °.
即小正六边形由图①位置滚动到图②位置时,线段绕点顺时针转过的角度为240度.
故应填:240.
三、面积的计算
例5如图5所示,正六边形内接于⊙,若⊙的半径为4,则阴影部分的面积等于 .
l幻)
分析及解答 该题考查了在外接圆中三角形、扇形和弓形的面积计算,该题的计算量较大,辅助线的添画也显得重要.具体解答如下:
连结、、.交于点交于点,过点作于点.
六边形是正六边形,
.
根据垂径定理,得.
在Rt中,,
,
.
于是有的面积.
同理的面积也是.
,半径,
是等边三角形,
.
在Rt 中,,
.
阴影部分的面积.
故应填:.
四、规律探索
例6 如图6,正六边形的边长为2,正六边形的外接圆与正六边形的各边相切,正六边形,的外接圆与正六边形的各边相切,…按这样的规律进行下去,的边长为( )21教育网
(A) (B) (C) (D)
分析及解答 该题的_è§???????è????????_用切线的性质、正多边形和其外接圆的关系.特别提示:正六边形的边长与其外接圆的半径相等!在作辅助线时,见切点,连圆心!具体解答如下:21·世纪*教育网
连结.
六边形是正六边形,
,
是等边三角形.
正六边形的外接圆与正六边形的各边相切,
,,
正六边形的边长为.
同理可求得正六边形的边长为.
故可得正六边形的边长为: ,故选D.
五、其它型题目
例7 如图7,已知点、、、、、是边长为1的正六边形的顶点,连结任意两点均得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为( )
(A) (B) (C) (D)
分析及解答 该题涉及到勾股定理、正六边形的性质和概率公式.具体解答如下:
不妨连结,过点作 ,垂足是点.
六边形是正六边形,
,
,.
可以发现:从任意一点,连结两点所得的所有线段一共有15种情况,而取得长度为的线段只有6种情况.
所以,在连结两点所得的所有线段中任取一条线段,取到长度为的线段的概率为.
故选B.
_21?????????è?????(www.21cnjy.com)_
“正六边形”考点透析
正六边形既是中_???????§°?????????_又是轴对称图形.在中考试题中,常考查到与之相关的线段、弧、面积、角的计算及规律探索等.现结合近年来的有关中考试题加以归类剖析.21·cn·jy·com
一、线段和弧的计算
例1 如图1,正六边形内接于⊙,半径为4,则这个正六边形的边心距和的长分别为( )www.21-cn-jy.com
(A) (B) (C) (D)
分析及解答 该题考查了正多边形和它的外接圆中的有关计算,主要应用正六边形的性质和弧长的公式进行计算.
具体解答如下:
连结.
根据勾股定理,得,
又的长度=.
故选D.
二、角的计算
例2 如图2,正六边形内接于⊙,若直线与⊙相切于点,则 =( )
(A)30° (B)35° (C)45° (D)60°
分析及解答 该题的解决主要是利用切线和正六边形的性质.具体解答如下:
连结,则是等边三角形,
.
又是⊙的切线,
,
.
故选A.
例3 平面上,将边长相等的正三角形、正方形、正五边形、正六边形
的一边重合并叠在一起,如图3,则= °.
分析及解答 该题的解决思路是求出特殊正多边形的每个内角是多少,进而求出所求的答案.具体解答如下:
正三角形的每个内角: ,
利用多边形的内角和公式分别求得正方形的每个内角是90°,
正五边形的每个内角是,
正六边形的每个内角是,
.
故应填:24.
例4 如图4,小正六边形沿着大正六边形的边缘顺时针滚动,小正六边形的边长是大正六边形边长的一半.当小正六边形由图①位置滚动到图②位置时,线段绕点顺时针转过的角度为 度.2·1·c·n·j·y
分析及解答 该题考查了正多边形与圆的关系,明确正六边形的中心角是60°是解决本题的关键.具体解答如下:
观察图形不难看出,
第一个到第二个转过了60°;
第二个到第三个转过了120°;
第三个到第四个又转过了60°,所以总共转动了240 °.
即小正六边形由图①位置滚动到图②位置时,线段绕点顺时针转过的角度为240度.
故应填:240.
三、面积的计算
例5如图5所示,正六边形内接于⊙,若⊙的半径为4,则阴影部分的面积等于 .
l幻)
分析及解答 该题考查了在外接圆中三角形、扇形和弓形的面积计算,该题的计算量较大,辅助线的添画也显得重要.具体解答如下:
连结、、.交于点交于点,过点作于点.
六边形是正六边形,
.
根据垂径定理,得.
在Rt中,,
,
.
于是有的面积.
同理的面积也是.
,半径,
是等边三角形,
.
在Rt 中,,
.
阴影部分的面积.
故应填:.
四、规律探索
例6 如图6,正六边形的边长为2,正六边形的外接圆与正六边形的各边相切,正六边形,的外接圆与正六边形的各边相切,…按这样的规律进行下去,的边长为( )21教育网
(A) (B) (C) (D)
分析及解答 该题的_è§???????è????????_用切线的性质、正多边形和其外接圆的关系.特别提示:正六边形的边长与其外接圆的半径相等!在作辅助线时,见切点,连圆心!具体解答如下:21·世纪*教育网
连结.
六边形是正六边形,
,
是等边三角形.
正六边形的外接圆与正六边形的各边相切,
,,
正六边形的边长为.
同理可求得正六边形的边长为.
故可得正六边形的边长为: ,故选D.
五、其它型题目
例7 如图7,已知点、、、、、是边长为1的正六边形的顶点,连结任意两点均得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为( )
(A) (B) (C) (D)
分析及解答 该题涉及到勾股定理、正六边形的性质和概率公式.具体解答如下:
不妨连结,过点作 ,垂足是点.
六边形是正六边形,
,
,.
可以发现:从任意一点,连结两点所得的所有线段一共有15种情况,而取得长度为的线段只有6种情况.
所以,在连结两点所得的所有线段中任取一条线段,取到长度为的线段的概率为.
故选B.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
