2021中考数学备考经典微专题 等腰三角形一个判定方法的证明及应用学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 等腰三角形一个判定方法的证明及应用学案(技巧+满分解答) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
等腰三角形一个判定方法的证明及应用
等腰三角形具有“三线合一”的性质:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
如图l,在中,是上一点.
(1)如果,那么;
(2)如果,那么,;
(3)如果,那么,.
图1
上述性质中,共存在4个关系式:.而改写后的每条性质都有两个条件,且都有一个条件是“”.
反过来,在关系式中,如果其中某两条成立,那么能否得到?
这是一个很有意义的话题,为了便于思考,现将它们罗列如下:
命题 在中,是上一点,
(1)如果,那么;
(2)如果,那么;
(3)如果,那么.
以上三个命题中,命题(1)可表述为:线段垂直平分线上的点到线段两端点的距离相等.证明简单.
命题(2)可通过≌证明.
而命题(3)用文字语言表达就是:
如果三角形一个角的平分线又是其对边上的中线,那么这个三角形是等腰三角形.
这是一个判定等腰_???è§?????????????_真命题,它有多种证法,而且这些证法几乎贯穿于整个初中阶段的几何学习.本文着重研究这个判定方法的证明及应用.
一、证明
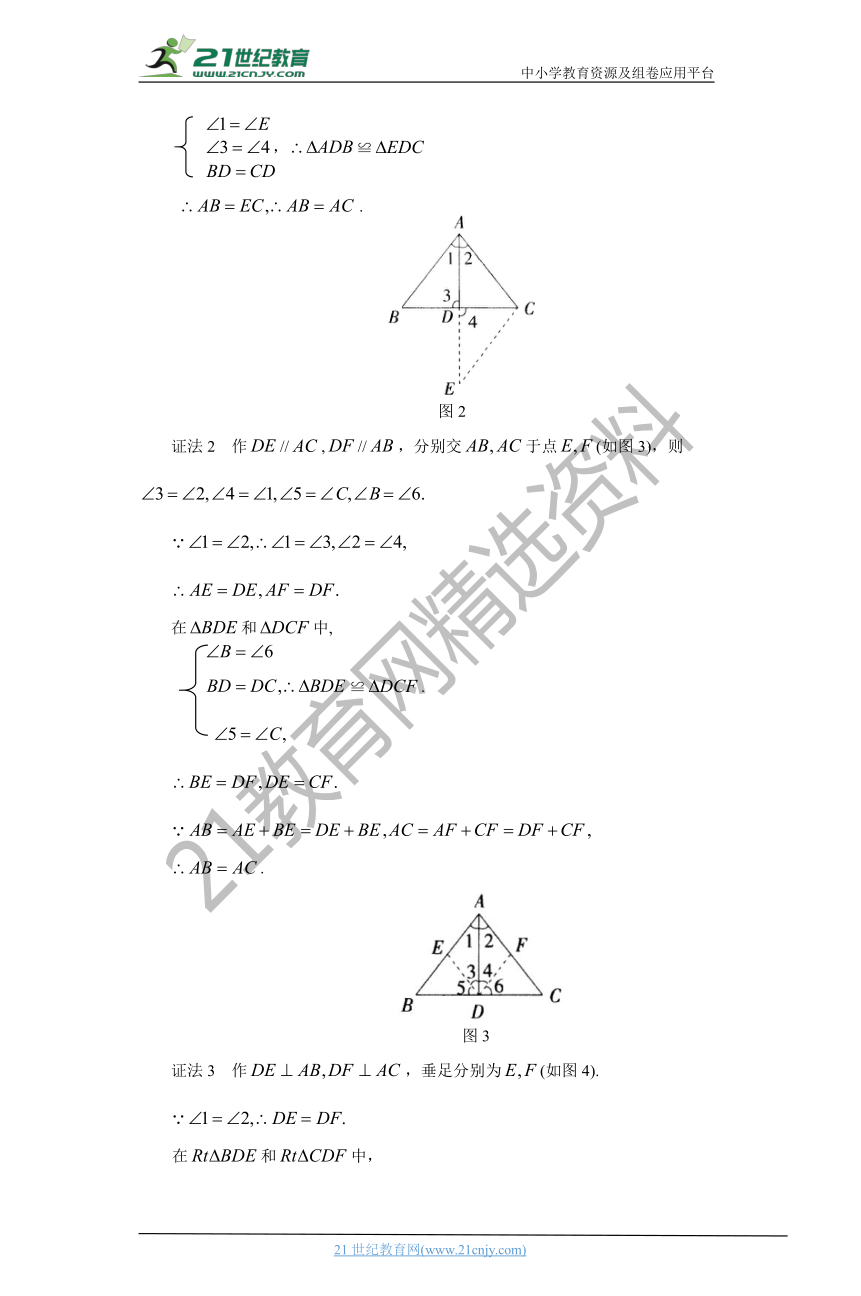
证法1 作 // ,交延长线于点(如图2),则.
在和中,
,≌
.
图2
证法2 作//,//,分别交于点(如图3),则
在和中,
≌.
.
图3
证法3 作,垂足分别为(如图4).
在和中,
,
,
≌,
.
图4
证法4 作,垂足分别为(如图4).
证法5 用反证法,假设>.在上取一点,使,连结(如图5).
在和中,
,
≌,
,
这与矛盾,
假设>不成立.
同理,<也不成立.
.
图5
证法6 延长到点,使,连结(如图6).
四边形是平行四边形,
∥
.
图6
证法7 作中点,连结(如图7).
是的中位线,
∥
.
图7
证法8 作的外接圆,延长交圆于点,连结( 如图8).
图8
二、应用
例1 如图9,在中,平分,求证:四边形是菱形.
证明 连结,交于点,则.
由于平分,由命题(3),得,是菱形.
图9
例2 已知:如图l0,是的角平分线,是中点,在上,且,求证:.
证明 取的中点,连结.
.
点是线段的三等分点,
图10
是的中点,
∥,亦即∥,∽,,
,即点是的中点.
平分 ,.
例3 已知:如图11 , 中,是的三等分线,求证:点不可能同时是边的三等分点.
图11
证明 假设点同时是线段的三等分点,则.
是的三等分线,.
由命题(3),得,.
两式相减,得,.
再由,立得,这与条件矛盾.
假设不成立,
点不可能同时是线段的三等分点.
_21?????????è?????(www.21cnjy.com)_
等腰三角形一个判定方法的证明及应用
等腰三角形具有“三线合一”的性质:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
如图l,在中,是上一点.
(1)如果,那么;
(2)如果,那么,;
(3)如果,那么,.
图1
上述性质中,共存在4个关系式:.而改写后的每条性质都有两个条件,且都有一个条件是“”.
反过来,在关系式中,如果其中某两条成立,那么能否得到?
这是一个很有意义的话题,为了便于思考,现将它们罗列如下:
命题 在中,是上一点,
(1)如果,那么;
(2)如果,那么;
(3)如果,那么.
以上三个命题中,命题(1)可表述为:线段垂直平分线上的点到线段两端点的距离相等.证明简单.
命题(2)可通过≌证明.
而命题(3)用文字语言表达就是:
如果三角形一个角的平分线又是其对边上的中线,那么这个三角形是等腰三角形.
这是一个判定等腰_???è§?????????????_真命题,它有多种证法,而且这些证法几乎贯穿于整个初中阶段的几何学习.本文着重研究这个判定方法的证明及应用.
一、证明
证法1 作 // ,交延长线于点(如图2),则.
在和中,
,≌
.
图2
证法2 作//,//,分别交于点(如图3),则
在和中,
≌.
.
图3
证法3 作,垂足分别为(如图4).
在和中,
,
,
≌,
.
图4
证法4 作,垂足分别为(如图4).
证法5 用反证法,假设>.在上取一点,使,连结(如图5).
在和中,
,
≌,
,
这与矛盾,
假设>不成立.
同理,<也不成立.
.
图5
证法6 延长到点,使,连结(如图6).
四边形是平行四边形,
∥
.
图6
证法7 作中点,连结(如图7).
是的中位线,
∥
.
图7
证法8 作的外接圆,延长交圆于点,连结( 如图8).
图8
二、应用
例1 如图9,在中,平分,求证:四边形是菱形.
证明 连结,交于点,则.
由于平分,由命题(3),得,是菱形.
图9
例2 已知:如图l0,是的角平分线,是中点,在上,且,求证:.
证明 取的中点,连结.
.
点是线段的三等分点,
图10
是的中点,
∥,亦即∥,∽,,
,即点是的中点.
平分 ,.
例3 已知:如图11 , 中,是的三等分线,求证:点不可能同时是边的三等分点.
图11
证明 假设点同时是线段的三等分点,则.
是的三等分线,.
由命题(3),得,.
两式相减,得,.
再由,立得,这与条件矛盾.
假设不成立,
点不可能同时是线段的三等分点.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
