1.2空间几何体的三视图和直观图 同步练习(含解析)
文档属性
| 名称 | 1.2空间几何体的三视图和直观图 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教新课标A版
必修二
1.2空间几何体的三视图和直观图
一、单选题
1.下列几何体各自的三视图中,有且仅有两个视图相同的是(???
)
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?②④
2.如图所示的图形中,是四棱锥的三视图的是( )
A.?????????????B.?????????????C.?????????????D.?
3.如图,正方体
中,
为棱
的中点,用过点
、
、
的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是(
??)
A.??????????????????B.??????????????????C.??????????????????D.?
4.如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是(
???)
A.?三棱锥????????????????????????????????B.?三棱柱????????????????????????????????C.?四棱锥????????????????????????????????D.?四棱柱
5.如图,
是水平放置的
的直观图,
,
,则
的面积是(???
)
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
6.如图,正方形
的边长为1cm,它是水平放置的一个平面图形用斜二测画法得到的直观图,则原图形的周长是(???
)
A.?8cm????????????????????????????B.?6cm????????????????????????????C.?????????????????????????????D.?
7.如图是一梯形OABC的直观图,其直观图面积为S,则梯形OABC的面积为(???
)
A.?2S????????????????????????????????????B.?S????????????????????????????????????C.?2
S????????????????????????????????????D.?S
8.一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则截去的几何体是
?
A.?三棱锥????????????????????????????????B.?三棱柱????????????????????????????????C.?四棱锥????????????????????????????????D.?四棱柱
9.如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为(???
)
A.?E???????????????????????????????????????????B.?F???????????????????????????????????????????C.?G???????????????????????????????????????????D.?H
10.如图所示,四边形
是上底为2,下底为6,底角为
的等腰梯形,用斜二测画法画出这个梯形的直观图
,在直观图中梯形的面积为(???
).
A.?4????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?8
11.已知空间几何体
是由圆柱切割而成的阴影部分构成,其中A,B为下底面圆直径的两个端点,C,D为上底面圆直径的两个端点,且
,圆柱底面半径是1,高是2,则空间几何体
可以无缝的穿过下列哪个图形(??
)
A.?椭圆???????????????????????????B.?等腰直角三角形???????????????????????????C.?正三角形???????????????????????????D.?正方形
12.某三棱锥的三视图如图所示,则这个三棱锥中最长的棱的长度为(???
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
二、填空题
13.已知某组合体的正视图与侧视图相同,如图所示,其中
,四边形
.为矩形,则该组合体的俯视图可以是________(把你认为正确的图的序号都填上).
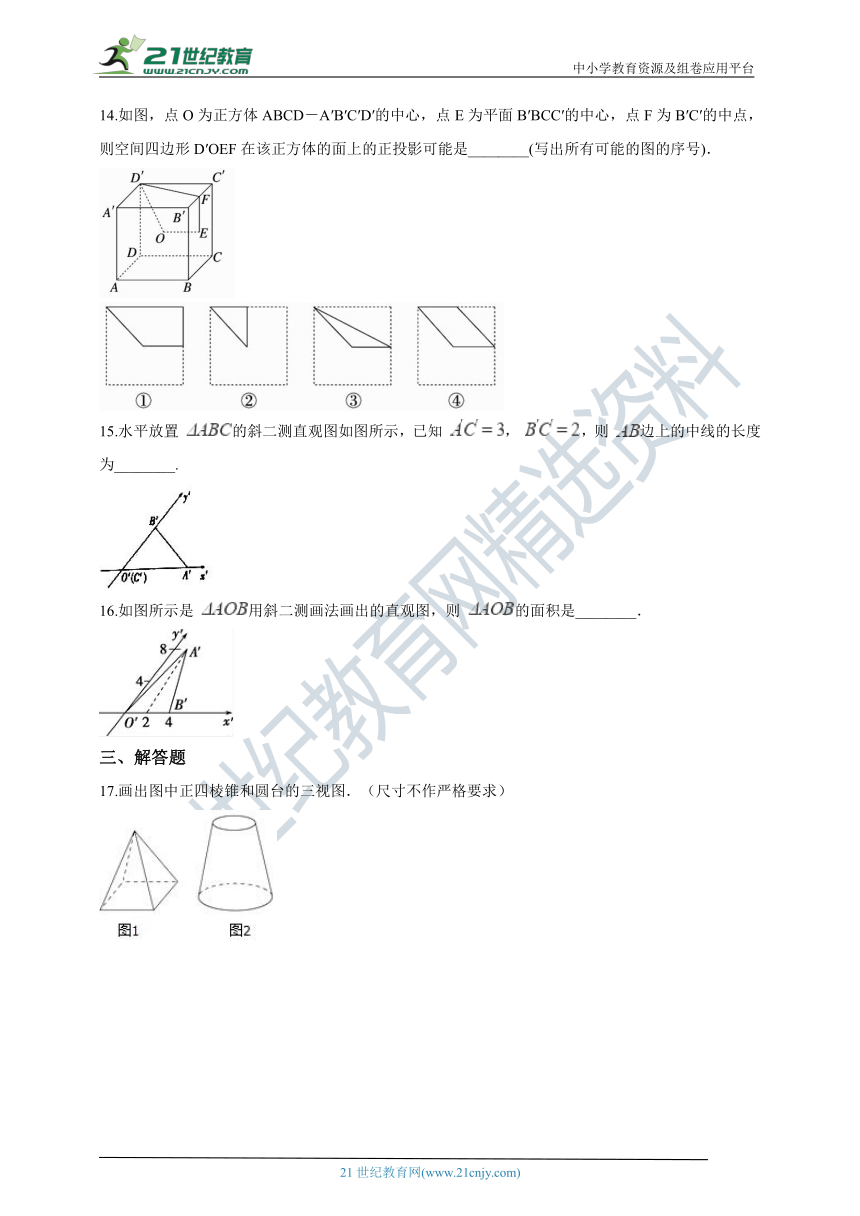
14.如图,点O为正方体ABCD-A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的面上的正投影可能是________(写出所有可能的图的序号).
15.水平放置
的斜二测直观图如图所示,已知
,
,则
边上的中线的长度为________.
16.如图所示是
用斜二测画法画出的直观图,则
的面积是________.
三、解答题
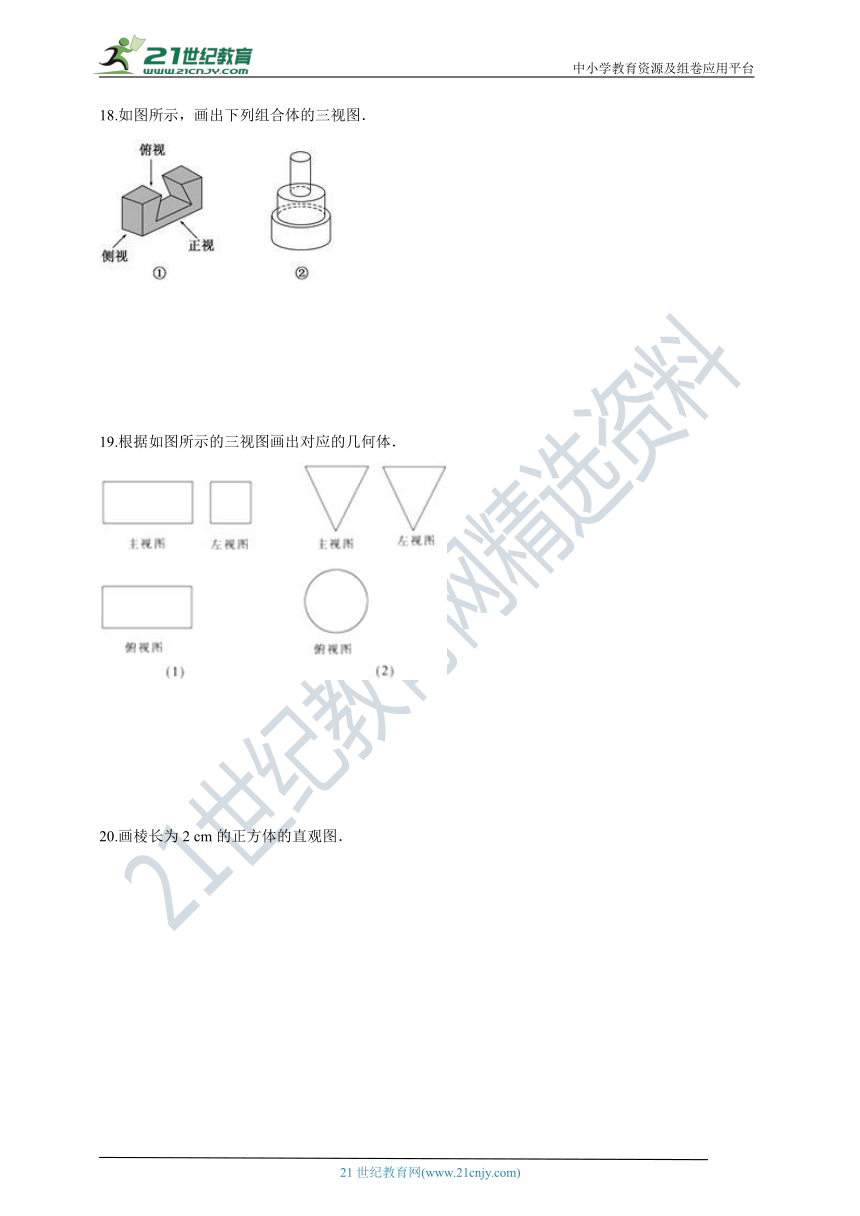
17.画出图中正四棱锥和圆台的三视图.(尺寸不作严格要求)
18.如图所示,画出下列组合体的三视图.
19.根据如图所示的三视图画出对应的几何体.
20.画棱长为2
cm的正方体的直观图.
21.如图所示,在平面直角坐标系中,各点坐标为O(0,0),A(1,3),B(3,1),C(4,6),D(2,5).试画出四边形ABCD的直观图.
22.如图所示,四边形ABCD是一个梯形,CD∥AB
,
CD=BO=1,△AOD为等腰直角三角形,O为AB的中点,试求梯形ABCD水平放置的直观图的面积.
答案解析部分
一、单选题
1.答案:
D
解:对①,三视图均相同;
对②,主视图与侧视图相同;
对③,三个视图均不相同;
对④,主视图和侧视图相同。
故答案为:D.
【分析】利用三视图的成图原理,即长对正、宽相等、高平齐,可得四个几何体的三视图。
2.答案:
B
解:棱锥的主视图、左视图都应该是三角形,所以排除选项C;
四棱锥的俯视图是连接对角线的矩形,所以选项B正确.
故答案为:B
【分析】锥体的主视图、左视图都是三角形,四棱锥的俯视图是四边形。
3.答案:
A
解:正方体
中,
过点
的平面截去该正方体的上半部分后,
剩余部分的直观图如图:
则该几何体的正视图为图中粗线部分.
故答案为:A.
【分析】由已知得到剩余部分的直观图,即可画出剩余几何体的正视图.
4.答案:
B
解:由三视图中的正视图可知,由一个面为直角三角形,左视图和俯视图可知其它的面为长方形,
综合可判断为三棱柱.
故答案为:B
【分析】利用三视图还原立体几何图形的方法得出该几何体为三棱柱。
5.答案:
C
解:由斜二测画法可知,
的实物图如下图所示:
可知
,
,且
,因此
的面积为
.
故答案为:C.
【分析】作出
的实物图,即可计算出
的面积.
6.答案:
A
解:将直观图还原为平面图形,如图所示.
=
,
,
所以
,
所以原图形的周长为8cm,
故答案为:A.
【分析】将直观图还原为平面图形是平行四边形,然后计算.
7.答案:
C
解:由
,
可得梯形OABC的面积
.
故答案为:C.
【分析】根据
,可得梯形OABC的面积.
8.答案:
B
解:由三视图可知,剩余几何体是如图所示的四棱柱
?,
则截去的部分是三棱柱
?,
故答案为:B.
【分析】利用已知条件结合三视图还原剩余几何体是四棱柱,则截去的部分是三棱柱。
9.答案:
A
解:根据三视图,画出多面体立体图形,
图中标出了根据三视图M点所在位置,
可知在侧视图中所对应的点为E
故答案为:A
【分析】根据三视图,画出多面体立体图形,即可求得M点在侧视图中对应的点.
10.答案:
B
解:如图:四边形
为等腰梯形,
则
,
,
所以
,
.
.
故答案为:B
【分析】由斜二测画法可知:直观图形的面积是原面积的
,所以只需求出原图形的面积即可求出直观图形的面积.
11.答案:
D
解:由题意可知
,且该几何体的高也是2,
A中,若椭圆的长轴长为2,短轴长小于2,则几何体无法穿过,
若椭圆的短轴长为2,长轴长大于2,则几何体穿过时有缝隙,均不符合题意;
B中,设
为
的中点,连接
,
,
则易证
为二面角
的平面角,
易求得
,而
,则
不是直角三角形,B不符合题意;
C中,由B中结论,
,
不是正三角形,C不符合题意;
D中,由题意,边长为2的正方形恰好和以
为直径的圆相切,D符合题意;
故答案为:D.
【分析】由题意可知
,且该几何体的高也是2,A中直接根据椭圆的几何性质可知A不符合题意;B、C中设
为
的中点,连接
,
,易得
既不是直角三角形,也不是正三角形,均不符合题意;D中边长为2的正方形恰好和以
为直径的圆相切,符合题意.
12.答案:
B
解:将几何体还原在长方体中,如图,
则该几何体即为
,
可得最长棱为长方体的一条体对角线
.
故选:B.
【分析】将几何体还原在长方体中即可找到最长的棱,计算即可得解.
二、填空题
13.答案:
①②③④
解:如图1,符合俯视图①;如图2,符合俯视图②;如图3,符合俯视图③;如图4,符合俯视图④.
【分析】根据正视图与俯视图,结合空间想象力,考虑锥体与柱体的组合体,即可的结果.
14.答案:①②③
解:图①为空间四边形D′OEF在前面(或后面)上的投影;
图②为空间四边形D′OEF在左面(或右面)上的投影;
图③为空间四边形D′OEF在上面(或下面)上的投影,图④不可能.
【分析】利用正投影的定义,即可得出结论。
15.答案:
解:在直观图中,
,
,
所以在
中,
,
,
为直角,
,因此边上的中线的长度为
.
故答案为:
.
【分析】由已知中直观图中线段的长,可分析出
实际为一个直角边长分别为3、4的直角三角形,进而根据勾股定理求出斜边,结合直角三角形斜边上的中线等于斜边的一半可得答案.
16.答案:
32
解:斜二测画法作图时,与
轴平行的线段长度不变,与
轴平行的线段长度变为原来的
,
由直观图可得:
.
故答案为:
【分析】根据斜二测画法的原则,结合题中直观图,可直接求出结果.
三、解答题
17.答案:解:画出图中正四棱锥的三视图,如图1;
画出图中圆台的三视图,如图2.
【分析】根据正四棱锥的三视图是两个全等的等腰三角形和有对角线的正方形,画出图1;根据圆台的三视图是两个全等的等腰梯形和两个同心圆,画出图2.
18.答案:
解:三视图如图①②所示.
【分析】根据几何体的三视图的规则,即可得到几何体的三视图.
19.答案:解:几何体直观图如图:
【分析】根据第一组三视图都是矩形判断几何体为长方体;根据第二组三视图的俯视图为圆,正视图与侧视图都是等腰三角形判断几何体为圆锥.
20.答案:解:①作水平放置的正方形的直观图ABCD,
使∠BAD=45°,AB=2
cm,AD=1
cm.
②过点A作z′轴,使∠BAz′=90°,
分别过点A,B,C,D,沿z′轴的正方向取AA1=BB1=CC1=DD1=2
cm.
③连接A1B1
,
B1C1
,
C1D1
,
D1A1如下图①,
擦去辅助线,把被遮住的线改为虚线,
得到的图形如下图②就是所求的正方体的直观图.
【分析】根据题意结合已知条件利用直观图与实际图形的转换特点:平行于x轴的长度不变,平行于y轴的长度变为原来的一半。首先作出水平放置的正方形的直观图,再作出垂直于平面的z轴结合平行于z轴的长度不变得到各个点的位置最后连接起来即可得到图形的直观图。
21.答案:解:画法:⑴先画x′轴和y′轴,使∠x′O′y′=45°(如图1).
⑵在原图中作AE⊥x轴,垂足为E(1,0).
⑶在x′轴上截取O′E′=OE,作A′E′∥y′轴,截取E′A′=1.5.
⑷同理确定点B′,C′,D′,其中B′G′=0.5,C′H′=3,D′F′=2.5.
⑸连线成图(去掉辅助线)(如图2).
【分析】每一点的横坐标不变,纵坐标减半,在连接四个点得到直观图形.
22.答案:解:在梯形ABCD中,AB=2,高OD=1,
梯形ABCD水平放置的直观图仍为梯形,
且上底CD和下底AB的长度都不变,
如图所示,
在直观图中,O′D′=
OD,梯形的高D′E′=
,
于是梯形A′B′C′D′的面积为
×(1+2)×
=
.
【分析】由斜二测画法规则,得到原图形与直观的面积的关系,求解.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教新课标A版
必修二
1.2空间几何体的三视图和直观图
一、单选题
1.下列几何体各自的三视图中,有且仅有两个视图相同的是(???
)
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?②④
2.如图所示的图形中,是四棱锥的三视图的是( )
A.?????????????B.?????????????C.?????????????D.?
3.如图,正方体
中,
为棱
的中点,用过点
、
、
的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是(
??)
A.??????????????????B.??????????????????C.??????????????????D.?
4.如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是(
???)
A.?三棱锥????????????????????????????????B.?三棱柱????????????????????????????????C.?四棱锥????????????????????????????????D.?四棱柱
5.如图,
是水平放置的
的直观图,
,
,则
的面积是(???
)
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
6.如图,正方形
的边长为1cm,它是水平放置的一个平面图形用斜二测画法得到的直观图,则原图形的周长是(???
)
A.?8cm????????????????????????????B.?6cm????????????????????????????C.?????????????????????????????D.?
7.如图是一梯形OABC的直观图,其直观图面积为S,则梯形OABC的面积为(???
)
A.?2S????????????????????????????????????B.?S????????????????????????????????????C.?2
S????????????????????????????????????D.?S
8.一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则截去的几何体是
?
A.?三棱锥????????????????????????????????B.?三棱柱????????????????????????????????C.?四棱锥????????????????????????????????D.?四棱柱
9.如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为(???
)
A.?E???????????????????????????????????????????B.?F???????????????????????????????????????????C.?G???????????????????????????????????????????D.?H
10.如图所示,四边形
是上底为2,下底为6,底角为
的等腰梯形,用斜二测画法画出这个梯形的直观图
,在直观图中梯形的面积为(???
).
A.?4????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?8
11.已知空间几何体
是由圆柱切割而成的阴影部分构成,其中A,B为下底面圆直径的两个端点,C,D为上底面圆直径的两个端点,且
,圆柱底面半径是1,高是2,则空间几何体
可以无缝的穿过下列哪个图形(??
)
A.?椭圆???????????????????????????B.?等腰直角三角形???????????????????????????C.?正三角形???????????????????????????D.?正方形
12.某三棱锥的三视图如图所示,则这个三棱锥中最长的棱的长度为(???
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
二、填空题
13.已知某组合体的正视图与侧视图相同,如图所示,其中
,四边形
.为矩形,则该组合体的俯视图可以是________(把你认为正确的图的序号都填上).
14.如图,点O为正方体ABCD-A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的面上的正投影可能是________(写出所有可能的图的序号).
15.水平放置
的斜二测直观图如图所示,已知
,
,则
边上的中线的长度为________.
16.如图所示是
用斜二测画法画出的直观图,则
的面积是________.
三、解答题
17.画出图中正四棱锥和圆台的三视图.(尺寸不作严格要求)
18.如图所示,画出下列组合体的三视图.
19.根据如图所示的三视图画出对应的几何体.
20.画棱长为2
cm的正方体的直观图.
21.如图所示,在平面直角坐标系中,各点坐标为O(0,0),A(1,3),B(3,1),C(4,6),D(2,5).试画出四边形ABCD的直观图.
22.如图所示,四边形ABCD是一个梯形,CD∥AB
,
CD=BO=1,△AOD为等腰直角三角形,O为AB的中点,试求梯形ABCD水平放置的直观图的面积.
答案解析部分
一、单选题
1.答案:
D
解:对①,三视图均相同;
对②,主视图与侧视图相同;
对③,三个视图均不相同;
对④,主视图和侧视图相同。
故答案为:D.
【分析】利用三视图的成图原理,即长对正、宽相等、高平齐,可得四个几何体的三视图。
2.答案:
B
解:棱锥的主视图、左视图都应该是三角形,所以排除选项C;
四棱锥的俯视图是连接对角线的矩形,所以选项B正确.
故答案为:B
【分析】锥体的主视图、左视图都是三角形,四棱锥的俯视图是四边形。
3.答案:
A
解:正方体
中,
过点
的平面截去该正方体的上半部分后,
剩余部分的直观图如图:
则该几何体的正视图为图中粗线部分.
故答案为:A.
【分析】由已知得到剩余部分的直观图,即可画出剩余几何体的正视图.
4.答案:
B
解:由三视图中的正视图可知,由一个面为直角三角形,左视图和俯视图可知其它的面为长方形,
综合可判断为三棱柱.
故答案为:B
【分析】利用三视图还原立体几何图形的方法得出该几何体为三棱柱。
5.答案:
C
解:由斜二测画法可知,
的实物图如下图所示:
可知
,
,且
,因此
的面积为
.
故答案为:C.
【分析】作出
的实物图,即可计算出
的面积.
6.答案:
A
解:将直观图还原为平面图形,如图所示.
=
,
,
所以
,
所以原图形的周长为8cm,
故答案为:A.
【分析】将直观图还原为平面图形是平行四边形,然后计算.
7.答案:
C
解:由
,
可得梯形OABC的面积
.
故答案为:C.
【分析】根据
,可得梯形OABC的面积.
8.答案:
B
解:由三视图可知,剩余几何体是如图所示的四棱柱
?,
则截去的部分是三棱柱
?,
故答案为:B.
【分析】利用已知条件结合三视图还原剩余几何体是四棱柱,则截去的部分是三棱柱。
9.答案:
A
解:根据三视图,画出多面体立体图形,
图中标出了根据三视图M点所在位置,
可知在侧视图中所对应的点为E
故答案为:A
【分析】根据三视图,画出多面体立体图形,即可求得M点在侧视图中对应的点.
10.答案:
B
解:如图:四边形
为等腰梯形,
则
,
,
所以
,
.
.
故答案为:B
【分析】由斜二测画法可知:直观图形的面积是原面积的
,所以只需求出原图形的面积即可求出直观图形的面积.
11.答案:
D
解:由题意可知
,且该几何体的高也是2,
A中,若椭圆的长轴长为2,短轴长小于2,则几何体无法穿过,
若椭圆的短轴长为2,长轴长大于2,则几何体穿过时有缝隙,均不符合题意;
B中,设
为
的中点,连接
,
,
则易证
为二面角
的平面角,
易求得
,而
,则
不是直角三角形,B不符合题意;
C中,由B中结论,
,
不是正三角形,C不符合题意;
D中,由题意,边长为2的正方形恰好和以
为直径的圆相切,D符合题意;
故答案为:D.
【分析】由题意可知
,且该几何体的高也是2,A中直接根据椭圆的几何性质可知A不符合题意;B、C中设
为
的中点,连接
,
,易得
既不是直角三角形,也不是正三角形,均不符合题意;D中边长为2的正方形恰好和以
为直径的圆相切,符合题意.
12.答案:
B
解:将几何体还原在长方体中,如图,
则该几何体即为
,
可得最长棱为长方体的一条体对角线
.
故选:B.
【分析】将几何体还原在长方体中即可找到最长的棱,计算即可得解.
二、填空题
13.答案:
①②③④
解:如图1,符合俯视图①;如图2,符合俯视图②;如图3,符合俯视图③;如图4,符合俯视图④.
【分析】根据正视图与俯视图,结合空间想象力,考虑锥体与柱体的组合体,即可的结果.
14.答案:①②③
解:图①为空间四边形D′OEF在前面(或后面)上的投影;
图②为空间四边形D′OEF在左面(或右面)上的投影;
图③为空间四边形D′OEF在上面(或下面)上的投影,图④不可能.
【分析】利用正投影的定义,即可得出结论。
15.答案:
解:在直观图中,
,
,
所以在
中,
,
,
为直角,
,因此边上的中线的长度为
.
故答案为:
.
【分析】由已知中直观图中线段的长,可分析出
实际为一个直角边长分别为3、4的直角三角形,进而根据勾股定理求出斜边,结合直角三角形斜边上的中线等于斜边的一半可得答案.
16.答案:
32
解:斜二测画法作图时,与
轴平行的线段长度不变,与
轴平行的线段长度变为原来的
,
由直观图可得:
.
故答案为:
【分析】根据斜二测画法的原则,结合题中直观图,可直接求出结果.
三、解答题
17.答案:解:画出图中正四棱锥的三视图,如图1;
画出图中圆台的三视图,如图2.
【分析】根据正四棱锥的三视图是两个全等的等腰三角形和有对角线的正方形,画出图1;根据圆台的三视图是两个全等的等腰梯形和两个同心圆,画出图2.
18.答案:
解:三视图如图①②所示.
【分析】根据几何体的三视图的规则,即可得到几何体的三视图.
19.答案:解:几何体直观图如图:
【分析】根据第一组三视图都是矩形判断几何体为长方体;根据第二组三视图的俯视图为圆,正视图与侧视图都是等腰三角形判断几何体为圆锥.
20.答案:解:①作水平放置的正方形的直观图ABCD,
使∠BAD=45°,AB=2
cm,AD=1
cm.
②过点A作z′轴,使∠BAz′=90°,
分别过点A,B,C,D,沿z′轴的正方向取AA1=BB1=CC1=DD1=2
cm.
③连接A1B1
,
B1C1
,
C1D1
,
D1A1如下图①,
擦去辅助线,把被遮住的线改为虚线,
得到的图形如下图②就是所求的正方体的直观图.
【分析】根据题意结合已知条件利用直观图与实际图形的转换特点:平行于x轴的长度不变,平行于y轴的长度变为原来的一半。首先作出水平放置的正方形的直观图,再作出垂直于平面的z轴结合平行于z轴的长度不变得到各个点的位置最后连接起来即可得到图形的直观图。
21.答案:解:画法:⑴先画x′轴和y′轴,使∠x′O′y′=45°(如图1).
⑵在原图中作AE⊥x轴,垂足为E(1,0).
⑶在x′轴上截取O′E′=OE,作A′E′∥y′轴,截取E′A′=1.5.
⑷同理确定点B′,C′,D′,其中B′G′=0.5,C′H′=3,D′F′=2.5.
⑸连线成图(去掉辅助线)(如图2).
【分析】每一点的横坐标不变,纵坐标减半,在连接四个点得到直观图形.
22.答案:解:在梯形ABCD中,AB=2,高OD=1,
梯形ABCD水平放置的直观图仍为梯形,
且上底CD和下底AB的长度都不变,
如图所示,
在直观图中,O′D′=
OD,梯形的高D′E′=
,
于是梯形A′B′C′D′的面积为
×(1+2)×
=
.
【分析】由斜二测画法规则,得到原图形与直观的面积的关系,求解.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
