人教版数学八年级上册14.2.1-平方差公式课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.2.1-平方差公式课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 589.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 07:47:43 | ||
图片预览






文档简介
(共19张PPT)
14.2.1
平方差公式
2、王捷同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王捷就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童!”王捷同学说:“过奖了,我只是利用了在数学上刚学过的一个公式.”
1、多项式乘以多项式的法则是什么?
1计算:
⑴
(x+1)(x-1)=______
;
⑵
(m+2)(m-2)=_____
;
⑶
(2x+3)(2x-3)=______.
观察上述算式,等号左边有什么规律?
观察计算结果,
你又发现了什么规律?
2猜想:(a
+
b)(a-
b)=——————.
a2-b2
(a+b)(a-b)
3证明:(1)代数
角度
(a
+
b)(a-
b)=a2-b2.
∴(a
+
b)(a-
b)=a2-b2.
(多项式乘法法则)
(合并同类项)
(a
+
b)
(a
-
b)
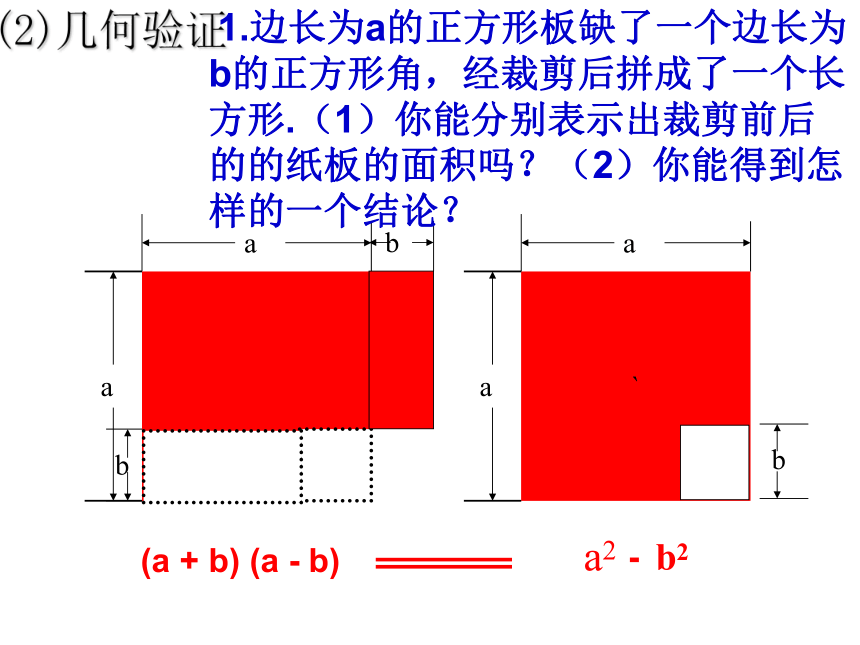
1.边长为a的正方形板缺了一个边长为b的正方形角,经裁剪后拼成了一个长方形.(1)你能分别表示出裁剪前后的的纸板的面积吗?(2)你能得到怎样的一个结论?
(2)几何验证
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
公式变形:
1、(a
–
b
)
(
a
+
b)
=
a2
-
b2
2、(b
+
a
)(
-b
+
a
)
=
a2
-
b2
例1:运用平方差公式计算:
(1)
(3x+2)(
3x-2
)
解:
(3x+2)(3x-2)
(a+
b)
(
a-
b)
=
a2
-
b2
=(3x)2-22
=
9x2-4
解:
(-x+3y)(x+3y)
=(3y-x)(3y+x)
=
(3y)2-x2
=
9y2-x2
a
b
a2-b2
结果
(a+b)(a-b)
1
x
12-x2
1-x2
-3
a
(-3)2-a2
9-a2
a
1
a2-12
a2-1
0.3x
1
1、填一填
(a+1)(a-1)
(0.3x+1)(0.3x-1)
(0.3x)2-12
0.09x2-1
快乐训练营第一站:C组,直接运用新知,解决第一层次问题
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
2、能否运用公式,若能直接说出结果
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)=
__________
(3)(-a-b)(-a+b)=
________
(4)(a-b)(-a-b)=
_________
(5)(a+b)(-a-b)=________
(6)(a-b)(-a+b)=________
a2-b2
a2-b2
b2-a2
b2-a2
快乐训练营第二站:B组,间接运用新知,解决第二层次问题
思考:平方差公式与整式的乘法有何关系?
不能
不能
平方差公式
(1)、结论:(a+b)(a-b)=
a2
–
b2
两数的和与它们的差的积,等于这两数的平方差。
①、有两个数是完全相同的,有两个数是相反的;
重点是观察它们的符号。
②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;
(3)、特点分析:
小明的计算正确吗?如果不正确应怎样改正?
(1)
(-3a-2)(3a-2)
=
9a2
-
4
(3)
(2a-3b)(3b+2a)
=
(2a-3b)(2a+3b)
=
4a2
-
3b
解:
改正:
(
)
(
)
(
)
=
(-2-3a)(-2+3a)
=
(-2)2
-
(3a)2
=
4
-
9a2
3、辨一辨
快乐训练营第三站:A组,灵活运用新知,解决第三层次问题。
例2
运用平方差公式计算:
(1)10.2×9.8
(2)
(y+2)
(y-2)
–
(y-1)
(y+5)
(3)(x+y)(x-y)(x2+y2)
(4)
解:10.2×9.8
=
=
=100-0.04
=99.96(元).
大家来比赛,看谁算得快
A组
(1)
103×97
(2)
60.2
×59.8
B组
(1)
1002-32
(2)
602-0.22
(1)
9991
(2)
3599.96
1.计算
20042
-
2003×2005;
解:
20042
-
2003×2005
=
20042
-
(2004-1)(2004+1)
=
20042
-
(20042-12
)
=
20042
-
20042+12
=1
2.计算:(2+1)(22+1)(24+1)…(232+1)+1
同桌间每人利用平方差公式出两道题,然后交换解答,找出对方做错的地方,并通过互助共同解决问题.
1.本节课你有何收获?
2.你还有什么疑问吗?
A组
习题14.2
复习巩固
T1
B组
习题14.2
综合运用
T3(4)
T5
C组
习题14.2
拓广探索
T9
1.计算
20042-2003×20052
2.请你利用平方差公式求出
(2+1)(22+1)(24+1)(28+1)……(264+1)的值.
3.
(a+b+c)(a-b-c)
寄语
如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!
14.2.1
平方差公式
2、王捷同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王捷就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童!”王捷同学说:“过奖了,我只是利用了在数学上刚学过的一个公式.”
1、多项式乘以多项式的法则是什么?
1计算:
⑴
(x+1)(x-1)=______
;
⑵
(m+2)(m-2)=_____
;
⑶
(2x+3)(2x-3)=______.
观察上述算式,等号左边有什么规律?
观察计算结果,
你又发现了什么规律?
2猜想:(a
+
b)(a-
b)=——————.
a2-b2
(a+b)(a-b)
3证明:(1)代数
角度
(a
+
b)(a-
b)=a2-b2.
∴(a
+
b)(a-
b)=a2-b2.
(多项式乘法法则)
(合并同类项)
(a
+
b)
(a
-
b)
1.边长为a的正方形板缺了一个边长为b的正方形角,经裁剪后拼成了一个长方形.(1)你能分别表示出裁剪前后的的纸板的面积吗?(2)你能得到怎样的一个结论?
(2)几何验证
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
公式变形:
1、(a
–
b
)
(
a
+
b)
=
a2
-
b2
2、(b
+
a
)(
-b
+
a
)
=
a2
-
b2
例1:运用平方差公式计算:
(1)
(3x+2)(
3x-2
)
解:
(3x+2)(3x-2)
(a+
b)
(
a-
b)
=
a2
-
b2
=(3x)2-22
=
9x2-4
解:
(-x+3y)(x+3y)
=(3y-x)(3y+x)
=
(3y)2-x2
=
9y2-x2
a
b
a2-b2
结果
(a+b)(a-b)
1
x
12-x2
1-x2
-3
a
(-3)2-a2
9-a2
a
1
a2-12
a2-1
0.3x
1
1、填一填
(a+1)(a-1)
(0.3x+1)(0.3x-1)
(0.3x)2-12
0.09x2-1
快乐训练营第一站:C组,直接运用新知,解决第一层次问题
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
2、能否运用公式,若能直接说出结果
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)=
__________
(3)(-a-b)(-a+b)=
________
(4)(a-b)(-a-b)=
_________
(5)(a+b)(-a-b)=________
(6)(a-b)(-a+b)=________
a2-b2
a2-b2
b2-a2
b2-a2
快乐训练营第二站:B组,间接运用新知,解决第二层次问题
思考:平方差公式与整式的乘法有何关系?
不能
不能
平方差公式
(1)、结论:(a+b)(a-b)=
a2
–
b2
两数的和与它们的差的积,等于这两数的平方差。
①、有两个数是完全相同的,有两个数是相反的;
重点是观察它们的符号。
②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;
(3)、特点分析:
小明的计算正确吗?如果不正确应怎样改正?
(1)
(-3a-2)(3a-2)
=
9a2
-
4
(3)
(2a-3b)(3b+2a)
=
(2a-3b)(2a+3b)
=
4a2
-
3b
解:
改正:
(
)
(
)
(
)
=
(-2-3a)(-2+3a)
=
(-2)2
-
(3a)2
=
4
-
9a2
3、辨一辨
快乐训练营第三站:A组,灵活运用新知,解决第三层次问题。
例2
运用平方差公式计算:
(1)10.2×9.8
(2)
(y+2)
(y-2)
–
(y-1)
(y+5)
(3)(x+y)(x-y)(x2+y2)
(4)
解:10.2×9.8
=
=
=100-0.04
=99.96(元).
大家来比赛,看谁算得快
A组
(1)
103×97
(2)
60.2
×59.8
B组
(1)
1002-32
(2)
602-0.22
(1)
9991
(2)
3599.96
1.计算
20042
-
2003×2005;
解:
20042
-
2003×2005
=
20042
-
(2004-1)(2004+1)
=
20042
-
(20042-12
)
=
20042
-
20042+12
=1
2.计算:(2+1)(22+1)(24+1)…(232+1)+1
同桌间每人利用平方差公式出两道题,然后交换解答,找出对方做错的地方,并通过互助共同解决问题.
1.本节课你有何收获?
2.你还有什么疑问吗?
A组
习题14.2
复习巩固
T1
B组
习题14.2
综合运用
T3(4)
T5
C组
习题14.2
拓广探索
T9
1.计算
20042-2003×20052
2.请你利用平方差公式求出
(2+1)(22+1)(24+1)(28+1)……(264+1)的值.
3.
(a+b+c)(a-b-c)
寄语
如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!
