人教版八年级数学上册第十三章《轴对称》13.2画轴对称图形同步练习题(word版,含答案)
文档属性
| 名称 | 人教版八年级数学上册第十三章《轴对称》13.2画轴对称图形同步练习题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 08:24:07 | ||
图片预览



文档简介
人教版八年级数学(上)第十三章《轴对称》13.2画轴对称图形同步练习题
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.如图,在平面直角坐标系中,正方形ABCD的顶点坐标分别是A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5……按此操作下去,则点P2019的坐标为(??
)。
A.(0,2)
B.(2,0)
C.(0,-2)
D.(-2,0)
2.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于y轴成轴对称的图形。若点A的坐标是(1,3),则点M和点N的坐标分别是(?
?)。
A.M(1,-3),N(-1,-3)
B.M(-1,-3),N(-1,3)
C.M(-1,-3),N(1,-3)
D.M(-1,3),N(1,-3)
3.坐标平面内有一个轴对称图形,、两点在此图形上互为对称点.若此图形上有一点C(-2,-9),则点C的对称点的坐标是(?
??)。
A.(-2,1)
B.
C.
D.(8,-9)
4.坐标平面内有点A(4,8),B(-4,-8),以坐标轴为对称轴,点A可以由点B经过m次轴对称变换得到,则m的最小值为(
)。
A.1
B.2
C.3
D.4
5.点A和点B(2,-3)关于x轴对称,则A,B两点间的距离是(
)。
A.4
B.5
C.6
D.10
6.小红同学误将点A的横纵坐标次序颠倒,写成A(a,b),另一学生误将点B的坐标写成关于y轴对称点的坐标,写成B(-b,-a);则A,B两点原来的位置关系是( )。
A.关于x轴对称
B.关于y轴对称
C.A和B重合
D.以上都不对
7.已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则∠P1OP2的度数是?
(??
)。
A.30°
B.45°
C.60°
D.90°
8.在平面直角坐标系中,点A(1,3)关于x轴对称点为A1,A1关于y轴对称点为A2,点A2的坐标为(
)
。
A.(-1,3)
B.(1,-3)
C.(3,1)
D.(-1,-3)
9.在平面直角坐标系内,点A(-5,8)和点B(-5,2)的对称轴是(
)。
A.x轴
B.y轴
C.直线y=5
D.直线x=-5
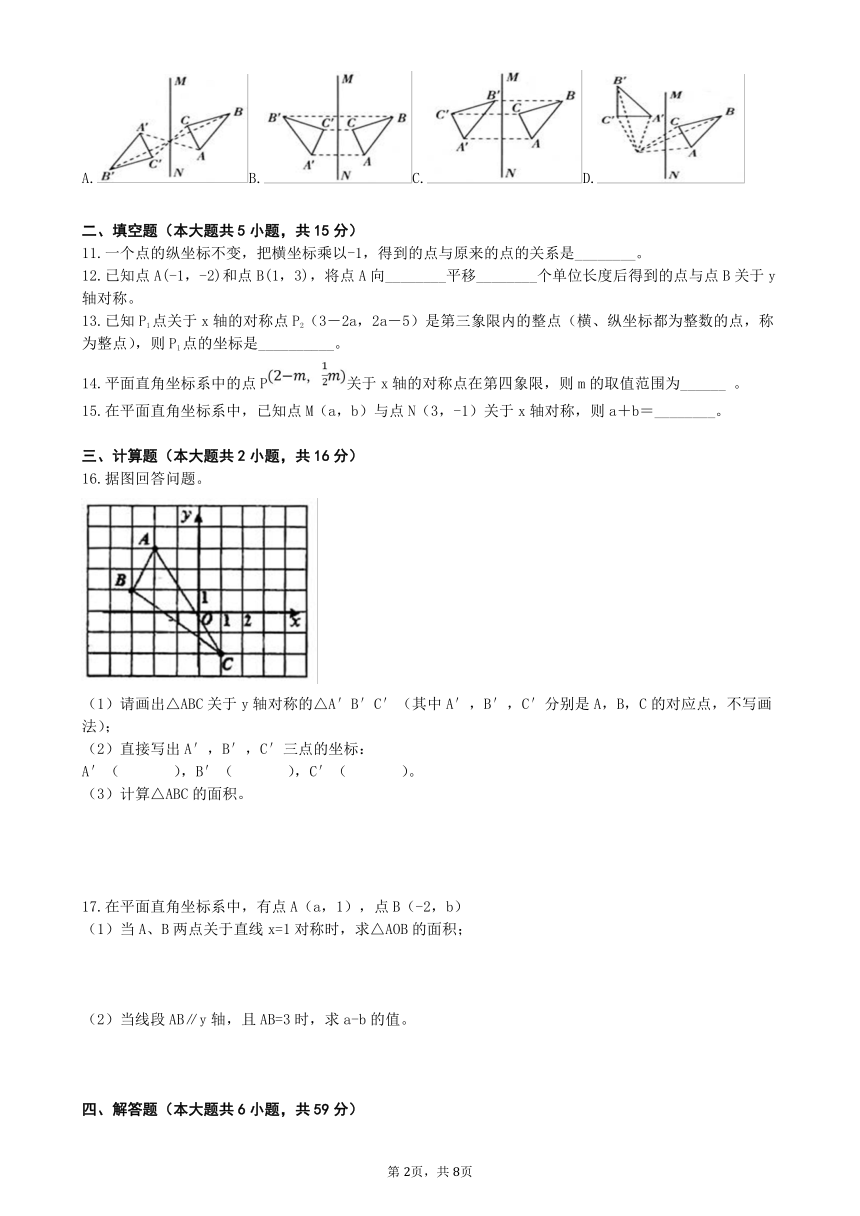
10.下面是四位同学作的△ABC关于直线MN的轴对称图形,其中正确的是(
?
?)。
A.B.C.D.
二、填空题(本大题共5小题,共15分)
11.一个点的纵坐标不变,把横坐标乘以-1,得到的点与原来的点的关系是________。
12.已知点A(-1,-2)和点B(1,3),将点A向________平移________个单位长度后得到的点与点B关于y轴对称。
13.已知P1点关于x轴的对称点P2(3-2a,2a-5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是__________。
14.平面直角坐标系中的点P关于x轴的对称点在第四象限,则m的取值范围为______
。
15.在平面直角坐标系中,已知点M(a,b)与点N(3,-1)关于x轴对称,则a+b=________。
三、计算题(本大题共2小题,共16分)
16.据图回答问题。
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:
A′(???
),B′(???
),C′(???
)。
(3)计算△ABC的面积。
17.在平面直角坐标系中,有点A(a,1),点B(-2,b)
(1)当A、B两点关于直线x=1对称时,求△AOB的面积;
(2)当线段AB∥y轴,且AB=3时,求a-b的值。
四、解答题(本大题共6小题,共59分)
18.如图,方格纸上画有AB,CD(点A,B,C,D是格点)两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法):
(1)请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;
(2)请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形(画出一种即可,图(1)的情况除外)。
19.如图,四边形ABCD各顶点的坐标分别为A(-2,3)、B(-3,1)、C(1,-2)、D(2,2).
(1)画出四边形ABCD关于y轴对称的四边形A′B′C′D′;
(2)求四边形ABCD的面积。
20.已知点M(2a-b,5+a),N(2b-1,-a+b)。
(1)若点M,N关于x轴对称,求a,b的值;
(2)若点M,N关于y轴对称,求(4a+b)2019的值。
21.如图,已知线段AB=2a(a>0),M是AB的中点,直线l1⊥AB于点A,直线l2⊥AB于点M,点P是l1左侧一点,P到l1的距离为b(a<b<2a)。
(1)作出点P关于l1的对称点P1,并在PP1上取一点P2,使点P2,P1关于l2对称;
(2)PP2与AB有何位置关系和数量关系,请说明理由。
22.已知线段AB,点A(1,3),点B(3,2),作出线段AB关于y轴对称的线段A1B1,求出A1,B1的坐标,比较A与A1和B与B1之间的坐标,你能得到什么结论?
23.如图,△ABC中,已知点A(–1,4),B(–2,2),C(1,1)。
(1)作△ABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标;
(2)作△ABC关于y轴对称的△A2B2C2,并写出点A2,B2,C2的坐标;
(3)观察点A1,B1,C1和A2,B2,C2的坐标,请用文字语言归纳点A1和A2,B1和B2,C1和C2坐标之间的关系。
参考答案
一、选择题(本大题共10小题,共30分)
1.D
2.C
3.A
4.B
5.C
6.A
7.C
8.D
9.C
10.B
二、填空题(本大题共5小题,共15分)
11.关于y轴对称
12.上;
5
13.(-1,1)
14.0<m<2
15.4
三、计算题(本大题共2小题,共16分)
16.(1)如图:
(2)2,3;3,1;-1,-2
(3)解:如下图,
用围补法可知,
S△ABC=4×5-×1×2-×4×3-×3×5
=20-1-6-7.5
=5.5
答:△ABC的面积是5.5。
17.解:(1)∵A、B关于直线x=1对称,
∴A、B的纵坐标相同,a-1=1-(-2)
∴b=1,a=4;
即A(4,1)、B(-2,1),
∴S△AOB=×6×1=3;
(2)当AB∥y轴时,有A、B的横坐标相同,
∴a=-2,
∵AB=3,
∴|b-1|=3,解得b=-2或b=4,
∴当a=-2,b=-2时,有a-b=0,
当a=-2,b=4时,有a-b=-6。
四、解答题(本大题共6小题,共59分)
18.解:(1)如图:
(2)如图所示。(答案不唯一)
?
19.解:(1)如图所示:
?(2)四边形ABCD的面积=5×5-×1×2-×1×4-×1×4-×3×4
=25-1-2-2-6
=14。
20.解:(1)由题意得:,解得:.
答:a,b的值分别为-8和-5。
(2)∵点M,N关于y轴对称,
∴,解得a=-1,b=3,
∴(4a+b)2019=-1。
21.解:(1)如图所示:
(2)PP2与AB平行且相等.
?证明如下:设PP1分别交l1,l2于点O1,O2,
∵P,P1关于l1对称,点P2在PP1上,
∴PP2⊥l1.又AB⊥l1,
∴PP2∥AB。
∵l1⊥AB,l2⊥AB,
∴l1∥l2。
∴四边形O1AMO2是长方形。
∴O1O2=AM=a。
∵P,P1关于l1对称,P1O1=PO1=b,P1,P2关于l2对称,
∴P2O2=P1O2=P1O1-O1O2=b-a。
∴PP2=PP1-P1P2=PP1-2P2O2=2b-2(b-a)=2a。
∴PP2与AB平行且相等。
22.解:如图:
由图可知:A1(-1,3),B1(-3,2),
?结论:关于y轴对称的两点,它们的横坐标互为相反数,纵坐标相同。
23.解:(1)如图所示,
∵A(–1,4),B(–2,2),C(1,1),A1,B1,C1和A,B,C关于x轴对称,
∴A1(–1,–4),B1(–2,–2),C1(1,–1);
(2)如图所示,
∵A(–1,4),B(–2,2),C(1,1),A2,B2,C2和A,B,C关于y轴对称,
∴A2(1,4),B2(2,2),C2(–1,1)?;
(3)根据(1)(2)中得出的坐标可知,A1和A2,B1和B2,C1和C2坐标之间的关系为:横坐标互为相反数,纵坐标也互为相反数。
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.如图,在平面直角坐标系中,正方形ABCD的顶点坐标分别是A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5……按此操作下去,则点P2019的坐标为(??
)。
A.(0,2)
B.(2,0)
C.(0,-2)
D.(-2,0)
2.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于y轴成轴对称的图形。若点A的坐标是(1,3),则点M和点N的坐标分别是(?
?)。
A.M(1,-3),N(-1,-3)
B.M(-1,-3),N(-1,3)
C.M(-1,-3),N(1,-3)
D.M(-1,3),N(1,-3)
3.坐标平面内有一个轴对称图形,、两点在此图形上互为对称点.若此图形上有一点C(-2,-9),则点C的对称点的坐标是(?
??)。
A.(-2,1)
B.
C.
D.(8,-9)
4.坐标平面内有点A(4,8),B(-4,-8),以坐标轴为对称轴,点A可以由点B经过m次轴对称变换得到,则m的最小值为(
)。
A.1
B.2
C.3
D.4
5.点A和点B(2,-3)关于x轴对称,则A,B两点间的距离是(
)。
A.4
B.5
C.6
D.10
6.小红同学误将点A的横纵坐标次序颠倒,写成A(a,b),另一学生误将点B的坐标写成关于y轴对称点的坐标,写成B(-b,-a);则A,B两点原来的位置关系是( )。
A.关于x轴对称
B.关于y轴对称
C.A和B重合
D.以上都不对
7.已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则∠P1OP2的度数是?
(??
)。
A.30°
B.45°
C.60°
D.90°
8.在平面直角坐标系中,点A(1,3)关于x轴对称点为A1,A1关于y轴对称点为A2,点A2的坐标为(
)
。
A.(-1,3)
B.(1,-3)
C.(3,1)
D.(-1,-3)
9.在平面直角坐标系内,点A(-5,8)和点B(-5,2)的对称轴是(
)。
A.x轴
B.y轴
C.直线y=5
D.直线x=-5
10.下面是四位同学作的△ABC关于直线MN的轴对称图形,其中正确的是(
?
?)。
A.B.C.D.
二、填空题(本大题共5小题,共15分)
11.一个点的纵坐标不变,把横坐标乘以-1,得到的点与原来的点的关系是________。
12.已知点A(-1,-2)和点B(1,3),将点A向________平移________个单位长度后得到的点与点B关于y轴对称。
13.已知P1点关于x轴的对称点P2(3-2a,2a-5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是__________。
14.平面直角坐标系中的点P关于x轴的对称点在第四象限,则m的取值范围为______
。
15.在平面直角坐标系中,已知点M(a,b)与点N(3,-1)关于x轴对称,则a+b=________。
三、计算题(本大题共2小题,共16分)
16.据图回答问题。
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:
A′(???
),B′(???
),C′(???
)。
(3)计算△ABC的面积。
17.在平面直角坐标系中,有点A(a,1),点B(-2,b)
(1)当A、B两点关于直线x=1对称时,求△AOB的面积;
(2)当线段AB∥y轴,且AB=3时,求a-b的值。
四、解答题(本大题共6小题,共59分)
18.如图,方格纸上画有AB,CD(点A,B,C,D是格点)两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法):
(1)请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;
(2)请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形(画出一种即可,图(1)的情况除外)。
19.如图,四边形ABCD各顶点的坐标分别为A(-2,3)、B(-3,1)、C(1,-2)、D(2,2).
(1)画出四边形ABCD关于y轴对称的四边形A′B′C′D′;
(2)求四边形ABCD的面积。
20.已知点M(2a-b,5+a),N(2b-1,-a+b)。
(1)若点M,N关于x轴对称,求a,b的值;
(2)若点M,N关于y轴对称,求(4a+b)2019的值。
21.如图,已知线段AB=2a(a>0),M是AB的中点,直线l1⊥AB于点A,直线l2⊥AB于点M,点P是l1左侧一点,P到l1的距离为b(a<b<2a)。
(1)作出点P关于l1的对称点P1,并在PP1上取一点P2,使点P2,P1关于l2对称;
(2)PP2与AB有何位置关系和数量关系,请说明理由。
22.已知线段AB,点A(1,3),点B(3,2),作出线段AB关于y轴对称的线段A1B1,求出A1,B1的坐标,比较A与A1和B与B1之间的坐标,你能得到什么结论?
23.如图,△ABC中,已知点A(–1,4),B(–2,2),C(1,1)。
(1)作△ABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标;
(2)作△ABC关于y轴对称的△A2B2C2,并写出点A2,B2,C2的坐标;
(3)观察点A1,B1,C1和A2,B2,C2的坐标,请用文字语言归纳点A1和A2,B1和B2,C1和C2坐标之间的关系。
参考答案
一、选择题(本大题共10小题,共30分)
1.D
2.C
3.A
4.B
5.C
6.A
7.C
8.D
9.C
10.B
二、填空题(本大题共5小题,共15分)
11.关于y轴对称
12.上;
5
13.(-1,1)
14.0<m<2
15.4
三、计算题(本大题共2小题,共16分)
16.(1)如图:
(2)2,3;3,1;-1,-2
(3)解:如下图,
用围补法可知,
S△ABC=4×5-×1×2-×4×3-×3×5
=20-1-6-7.5
=5.5
答:△ABC的面积是5.5。
17.解:(1)∵A、B关于直线x=1对称,
∴A、B的纵坐标相同,a-1=1-(-2)
∴b=1,a=4;
即A(4,1)、B(-2,1),
∴S△AOB=×6×1=3;
(2)当AB∥y轴时,有A、B的横坐标相同,
∴a=-2,
∵AB=3,
∴|b-1|=3,解得b=-2或b=4,
∴当a=-2,b=-2时,有a-b=0,
当a=-2,b=4时,有a-b=-6。
四、解答题(本大题共6小题,共59分)
18.解:(1)如图:
(2)如图所示。(答案不唯一)
?
19.解:(1)如图所示:
?(2)四边形ABCD的面积=5×5-×1×2-×1×4-×1×4-×3×4
=25-1-2-2-6
=14。
20.解:(1)由题意得:,解得:.
答:a,b的值分别为-8和-5。
(2)∵点M,N关于y轴对称,
∴,解得a=-1,b=3,
∴(4a+b)2019=-1。
21.解:(1)如图所示:
(2)PP2与AB平行且相等.
?证明如下:设PP1分别交l1,l2于点O1,O2,
∵P,P1关于l1对称,点P2在PP1上,
∴PP2⊥l1.又AB⊥l1,
∴PP2∥AB。
∵l1⊥AB,l2⊥AB,
∴l1∥l2。
∴四边形O1AMO2是长方形。
∴O1O2=AM=a。
∵P,P1关于l1对称,P1O1=PO1=b,P1,P2关于l2对称,
∴P2O2=P1O2=P1O1-O1O2=b-a。
∴PP2=PP1-P1P2=PP1-2P2O2=2b-2(b-a)=2a。
∴PP2与AB平行且相等。
22.解:如图:
由图可知:A1(-1,3),B1(-3,2),
?结论:关于y轴对称的两点,它们的横坐标互为相反数,纵坐标相同。
23.解:(1)如图所示,
∵A(–1,4),B(–2,2),C(1,1),A1,B1,C1和A,B,C关于x轴对称,
∴A1(–1,–4),B1(–2,–2),C1(1,–1);
(2)如图所示,
∵A(–1,4),B(–2,2),C(1,1),A2,B2,C2和A,B,C关于y轴对称,
∴A2(1,4),B2(2,2),C2(–1,1)?;
(3)根据(1)(2)中得出的坐标可知,A1和A2,B1和B2,C1和C2坐标之间的关系为:横坐标互为相反数,纵坐标也互为相反数。
第2页,共2页
第1页,共1页
