人教版八年级数学 上 册 11.2与三角形有关的角 同步练习题(word 版 含答案)
文档属性
| 名称 | 人教版八年级数学 上 册 11.2与三角形有关的角 同步练习题(word 版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览


文档简介
人教版八年级数学(上)第十一章《三角形》11.2与三角形有关的角同步练习题
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.如图,下列各角为△ABC的外角的是(
)。
A.∠1
B.∠2
C.∠3
D.∠4
2.在△ABC中,,则此三角形是(
)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
3.如图,∠DBA和∠ACE是△ABC的外角,则∠DBA+∠ACE等于(
)。
A.180°
B.180°-∠A
C.180°+∠A
D.以上答案都不对
第3题图
第4题图
第5题图
4.已知a∥b,一块含30°角的直角三角尺按如图所示的方式放置,∠2=45°,则∠1的度数为(
)。
A.100°
B.135°
C.155°
D.165°
5.如图,AB
//
CD,∠A=50°,∠C=30°,则∠AEC等于(
)。
A.20°
B.50°
C.80°
D.100°
6.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=50°,则∠BPC的度数是(
)。
A.100°
B.120°
C.130°
D.150°
第6题图
第7题图
7.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A等于(
)。
A.35°
B.95°
C.85°
D.75°
8.如图,在△ABC中,∠A=60°,∠B=40°则∠C的度数为(
)。
A.100°
B.80°
C.60°
D.40°
9.下列说法正确的是(
)。
A.三角形的内角中最多有一个锐角
B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角
D.三角形的三个内角都大于60°
10.如图,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,则∠FBA的度数为(?
?)。
A.50°
B.60°
C.70°
D.80°
第8题图
第10题图
第11题图
二、填空题(本大题共5小题,共15分)
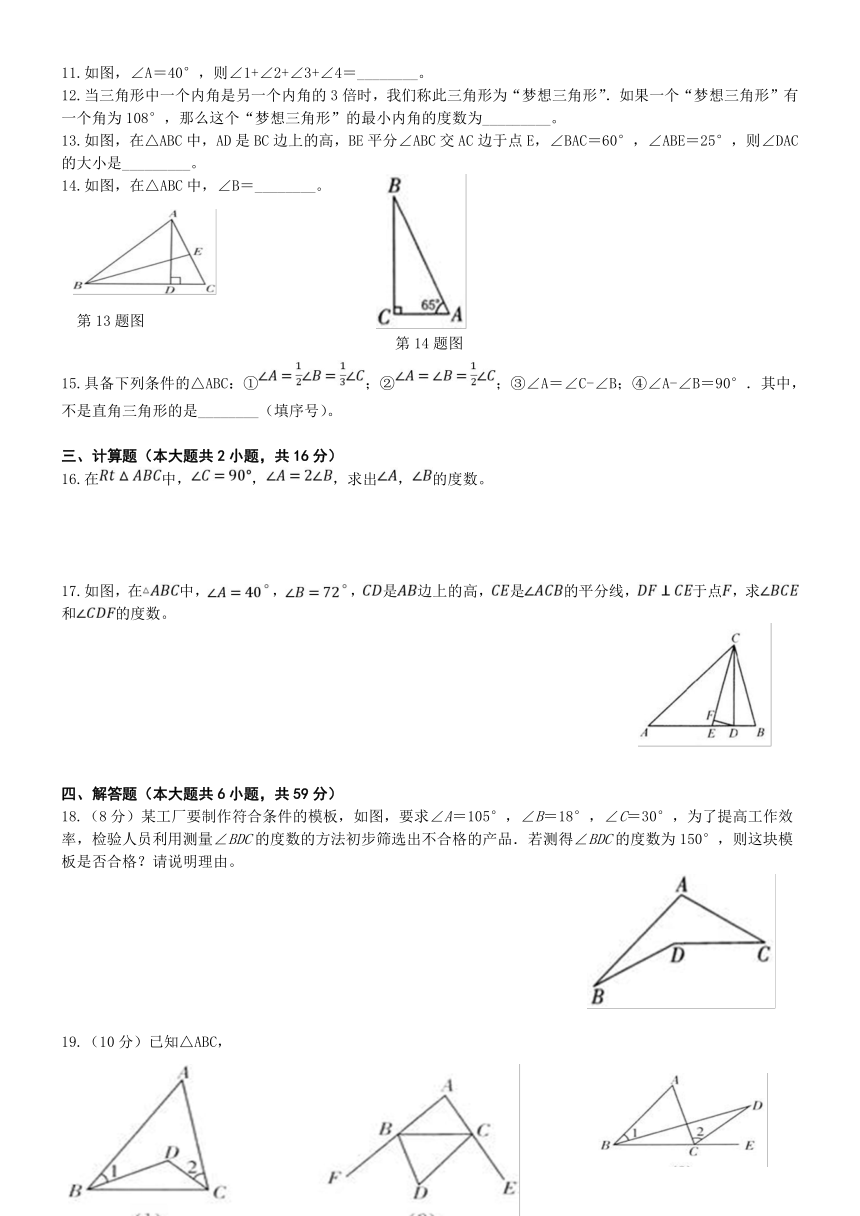
11.如图,∠A=40°,则∠1+∠2+∠3+∠4=________。
12.当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_________。
13.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是_________。
14.如图,在△ABC中,∠B=________。
第13题图
第14题图
15.具备下列条件的△ABC:①;②;③∠A=∠C-∠B;④∠A-∠B=90°.其中,不是直角三角形的是________(填序号)。
三、计算题(本大题共2小题,共16分)
16.在中,,,求出,的度数。
17.如图,在中,,,是边上的高,是的平分线,于点,求和的度数。
四、解答题(本大题共6小题,共59分)
18.(8分)某工厂要制作符合条件的模板,如图,要求∠A=105°,∠B=18°,∠C=30°,为了提高工作效率,检验人员利用测量∠BDC的度数的方法初步筛选出不合格的产品.若测得∠BDC的度数为150°,则这块模板是否合格?请说明理由。
19.(10分)已知△ABC,
(1)如图(1),若点D是△ABC内任一点、求证:∠D=∠A+∠ABD+∠ACD。
(2)若点D是△ABC外一点,位置如图(2)所示.猜想∠D,∠A,∠ABD,∠ACD有怎样的关系?请直接写出所满足的解析式。(不需要证明)
(3)若点D是△ABC外一点,位置如图(3)所示、猜想∠D,∠A,∠ABD,∠ACD之间有怎样的关系,并证明你的结论。
20.(9分)如图,在Rt△ABC中,∠C=90?,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P。
(1)求∠APD的度数;
(2)若∠BDC=58?,求∠BAP的度数。
21.(10分)如图,在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
(1)填写下面的表格.
∠A的度数
50°
60°
70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
22.(9分)如图,在某海面上,客轮C突然发生事故,马上向救护船B发出求救信号.由于救护船A离客轮C比救护船B离客轮C要近,所以救护船B立即向救护船A发出信号,让其救助客轮C.已知救护船A在救护船B的北偏东45°方向上,客轮C在救护船B的北偏东75°方向上,经测得∠ACB=75°,则救护船A沿南偏东多少度方向驶向客轮C所用的时间最短?
23.(13分)直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小;
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是
∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值。
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的4倍,请直接写出∠ABO的度数。
参考答案
一、选择题(本大题共10小题,共30分)
1.C
2.B
3.C
4.D
5.C
6.C
7.C
8.B
9.C
10.C
二、填空题(本大题共5小题,共15分)
11.280°
12.?36°或18°
13.20°
14.25°
15.④
三、计算题(本大题共2小题,共16分)
16.解:∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°;
∵∠A=2∠B,
∴2∠B+∠B=90°,
∴3∠B=90°,
解得∠B=30°,
∴∠A=90°-30°=60°,
综上,可得
∠A=60°,∠B=30°.
17.解:∵∠A=40°,∠B=72°,
∴∠ACB=180°-40°-72°=68°.
∵CE是∠ACB的平分线,
∴∠BCE=∠ACB=×68°=34°.
∵CD⊥AB即∠CDB=90°,
∴∠BCD=180°-90°-72°=18°,
∴∠DCE=∠BCE-∠BCD=34°-18°=16°.
∵DF⊥CE即∠DFC=90°,
∴∠CDF=180°-90°-16°=74°.
四、解答题(本大题共6小题,共59分)
18.解:这块模板不合格,
理由:如图,延长BD交AC于点E,
由三角形外角的性质,可得∠DEC=∠A+∠B,∠BDC=∠DEC+∠C,
∴∠BDC=∠A+∠B+∠C=105°+18°+30°=153°≠150°.
∴这块模板不合格。
19.解:(1)延长BD交AC于点E,
∵∠BDC是△CDE的外角,
∴∠BDC=∠2+∠CED,
∵∠CED是△ABE的外角,
∴∠CED=∠A+∠1.
∴∠BDC=∠A+∠1+∠2,
即∠D=∠A+∠ABD+∠ACD;
(2)∵∠D+∠A+∠ABD+∠ACD=∠A+∠ABC+∠ACB+∠D+∠DBC+∠DCB,∠A+∠ABC+∠ACB=180°,∠D+∠DBC+∠DCB=180°,
∴∠D+∠A+∠ABD+∠ACD=360°;
(3)令BD,AC的交点为F,
∵∠AFD是△ABF的外角,
∴∠AFD=∠1+∠A,
∵∠AFD是△CDF的外角,
∴∠AFD=∠D+∠2,
∴∠A+∠1=∠D+∠2,
即∠D+∠ACD=∠A+∠ABD。
20.解:(1)∵∠C=90°,
∴∠ABC+∠BAC=90°,
∴.
∵BD平分∠ABC,AP平分∠BAC,
∴,
∴∠APD=∠BAP+∠ABP=45°;
(2)∵∠BDC=58°,
∴∠DBC=90°-∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠BAP=∠APD-∠ABD=45°-32°=13°。
21.解:(1)
∠A的度数
50°
60°
70°
∠BOC的度数
115°
120°
125°
(2)猜想:∠BOC=90°+∠A.
理由:∵在△ABC中,OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠ABC+∠ACB=180°-∠A,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-∠A)=90°+∠A。
22.解:∵∠NBA=45°,∠NBC=75°,
?
?
?
∠ABC=30°,
??
?∵NB∥AS,
??
?∴∠BAS=45°,
??
?∵∠ACB=75°
?
?∴
∠SAC=180°-∠ACB-∠ABC-∠BAS=30°
?
?∴救护船A应沿南偏东30°方向驶向客轮C所用时间最短。
23.解:(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变。
延长AD、BC交于点F。
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=∠BAP,∠ABC=∠ABM,
∴∠BAD+∠ABC=(∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO,∠EOQ=∠BOQ,
∴∠E=∠EOQ-∠EAO=(∠BOQ-∠BAO)=∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°。
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°;
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°。
∴∠ABO为60°或45°。
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.如图,下列各角为△ABC的外角的是(
)。
A.∠1
B.∠2
C.∠3
D.∠4
2.在△ABC中,,则此三角形是(
)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
3.如图,∠DBA和∠ACE是△ABC的外角,则∠DBA+∠ACE等于(
)。
A.180°
B.180°-∠A
C.180°+∠A
D.以上答案都不对
第3题图
第4题图
第5题图
4.已知a∥b,一块含30°角的直角三角尺按如图所示的方式放置,∠2=45°,则∠1的度数为(
)。
A.100°
B.135°
C.155°
D.165°
5.如图,AB
//
CD,∠A=50°,∠C=30°,则∠AEC等于(
)。
A.20°
B.50°
C.80°
D.100°
6.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=50°,则∠BPC的度数是(
)。
A.100°
B.120°
C.130°
D.150°
第6题图
第7题图
7.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A等于(
)。
A.35°
B.95°
C.85°
D.75°
8.如图,在△ABC中,∠A=60°,∠B=40°则∠C的度数为(
)。
A.100°
B.80°
C.60°
D.40°
9.下列说法正确的是(
)。
A.三角形的内角中最多有一个锐角
B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角
D.三角形的三个内角都大于60°
10.如图,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,则∠FBA的度数为(?
?)。
A.50°
B.60°
C.70°
D.80°
第8题图
第10题图
第11题图
二、填空题(本大题共5小题,共15分)
11.如图,∠A=40°,则∠1+∠2+∠3+∠4=________。
12.当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_________。
13.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是_________。
14.如图,在△ABC中,∠B=________。
第13题图
第14题图
15.具备下列条件的△ABC:①;②;③∠A=∠C-∠B;④∠A-∠B=90°.其中,不是直角三角形的是________(填序号)。
三、计算题(本大题共2小题,共16分)
16.在中,,,求出,的度数。
17.如图,在中,,,是边上的高,是的平分线,于点,求和的度数。
四、解答题(本大题共6小题,共59分)
18.(8分)某工厂要制作符合条件的模板,如图,要求∠A=105°,∠B=18°,∠C=30°,为了提高工作效率,检验人员利用测量∠BDC的度数的方法初步筛选出不合格的产品.若测得∠BDC的度数为150°,则这块模板是否合格?请说明理由。
19.(10分)已知△ABC,
(1)如图(1),若点D是△ABC内任一点、求证:∠D=∠A+∠ABD+∠ACD。
(2)若点D是△ABC外一点,位置如图(2)所示.猜想∠D,∠A,∠ABD,∠ACD有怎样的关系?请直接写出所满足的解析式。(不需要证明)
(3)若点D是△ABC外一点,位置如图(3)所示、猜想∠D,∠A,∠ABD,∠ACD之间有怎样的关系,并证明你的结论。
20.(9分)如图,在Rt△ABC中,∠C=90?,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P。
(1)求∠APD的度数;
(2)若∠BDC=58?,求∠BAP的度数。
21.(10分)如图,在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
(1)填写下面的表格.
∠A的度数
50°
60°
70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
22.(9分)如图,在某海面上,客轮C突然发生事故,马上向救护船B发出求救信号.由于救护船A离客轮C比救护船B离客轮C要近,所以救护船B立即向救护船A发出信号,让其救助客轮C.已知救护船A在救护船B的北偏东45°方向上,客轮C在救护船B的北偏东75°方向上,经测得∠ACB=75°,则救护船A沿南偏东多少度方向驶向客轮C所用的时间最短?
23.(13分)直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小;
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是
∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值。
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的4倍,请直接写出∠ABO的度数。
参考答案
一、选择题(本大题共10小题,共30分)
1.C
2.B
3.C
4.D
5.C
6.C
7.C
8.B
9.C
10.C
二、填空题(本大题共5小题,共15分)
11.280°
12.?36°或18°
13.20°
14.25°
15.④
三、计算题(本大题共2小题,共16分)
16.解:∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°;
∵∠A=2∠B,
∴2∠B+∠B=90°,
∴3∠B=90°,
解得∠B=30°,
∴∠A=90°-30°=60°,
综上,可得
∠A=60°,∠B=30°.
17.解:∵∠A=40°,∠B=72°,
∴∠ACB=180°-40°-72°=68°.
∵CE是∠ACB的平分线,
∴∠BCE=∠ACB=×68°=34°.
∵CD⊥AB即∠CDB=90°,
∴∠BCD=180°-90°-72°=18°,
∴∠DCE=∠BCE-∠BCD=34°-18°=16°.
∵DF⊥CE即∠DFC=90°,
∴∠CDF=180°-90°-16°=74°.
四、解答题(本大题共6小题,共59分)
18.解:这块模板不合格,
理由:如图,延长BD交AC于点E,
由三角形外角的性质,可得∠DEC=∠A+∠B,∠BDC=∠DEC+∠C,
∴∠BDC=∠A+∠B+∠C=105°+18°+30°=153°≠150°.
∴这块模板不合格。
19.解:(1)延长BD交AC于点E,
∵∠BDC是△CDE的外角,
∴∠BDC=∠2+∠CED,
∵∠CED是△ABE的外角,
∴∠CED=∠A+∠1.
∴∠BDC=∠A+∠1+∠2,
即∠D=∠A+∠ABD+∠ACD;
(2)∵∠D+∠A+∠ABD+∠ACD=∠A+∠ABC+∠ACB+∠D+∠DBC+∠DCB,∠A+∠ABC+∠ACB=180°,∠D+∠DBC+∠DCB=180°,
∴∠D+∠A+∠ABD+∠ACD=360°;
(3)令BD,AC的交点为F,
∵∠AFD是△ABF的外角,
∴∠AFD=∠1+∠A,
∵∠AFD是△CDF的外角,
∴∠AFD=∠D+∠2,
∴∠A+∠1=∠D+∠2,
即∠D+∠ACD=∠A+∠ABD。
20.解:(1)∵∠C=90°,
∴∠ABC+∠BAC=90°,
∴.
∵BD平分∠ABC,AP平分∠BAC,
∴,
∴∠APD=∠BAP+∠ABP=45°;
(2)∵∠BDC=58°,
∴∠DBC=90°-∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠BAP=∠APD-∠ABD=45°-32°=13°。
21.解:(1)
∠A的度数
50°
60°
70°
∠BOC的度数
115°
120°
125°
(2)猜想:∠BOC=90°+∠A.
理由:∵在△ABC中,OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠ABC+∠ACB=180°-∠A,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-∠A)=90°+∠A。
22.解:∵∠NBA=45°,∠NBC=75°,
?
?
?
∠ABC=30°,
??
?∵NB∥AS,
??
?∴∠BAS=45°,
??
?∵∠ACB=75°
?
?∴
∠SAC=180°-∠ACB-∠ABC-∠BAS=30°
?
?∴救护船A应沿南偏东30°方向驶向客轮C所用时间最短。
23.解:(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变。
延长AD、BC交于点F。
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=∠BAP,∠ABC=∠ABM,
∴∠BAD+∠ABC=(∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO,∠EOQ=∠BOQ,
∴∠E=∠EOQ-∠EAO=(∠BOQ-∠BAO)=∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°。
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°;
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°。
∴∠ABO为60°或45°。
第2页,共2页
第1页,共1页
