苏科版数学八年级上册 第一章 全等三角形单元测试四(word版,含答案)
文档属性
| 名称 | 苏科版数学八年级上册 第一章 全等三角形单元测试四(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 949.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览


文档简介
第一章《全等三角形》综合测试卷
(4)
(考试时间:90分钟
满分:100分)
一、选择题(每题3分,共24分)
1.如图,于点,于点,平分,则的理由是(
)
A.
SAS
B.
AAS
C.
SSS
D.
HL
2.如图,,,,下列条件中,不能判断的是(
)
A.
B.
C.
D.
3.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是(
)
A.
15
B.
30
C.
45
D.
60
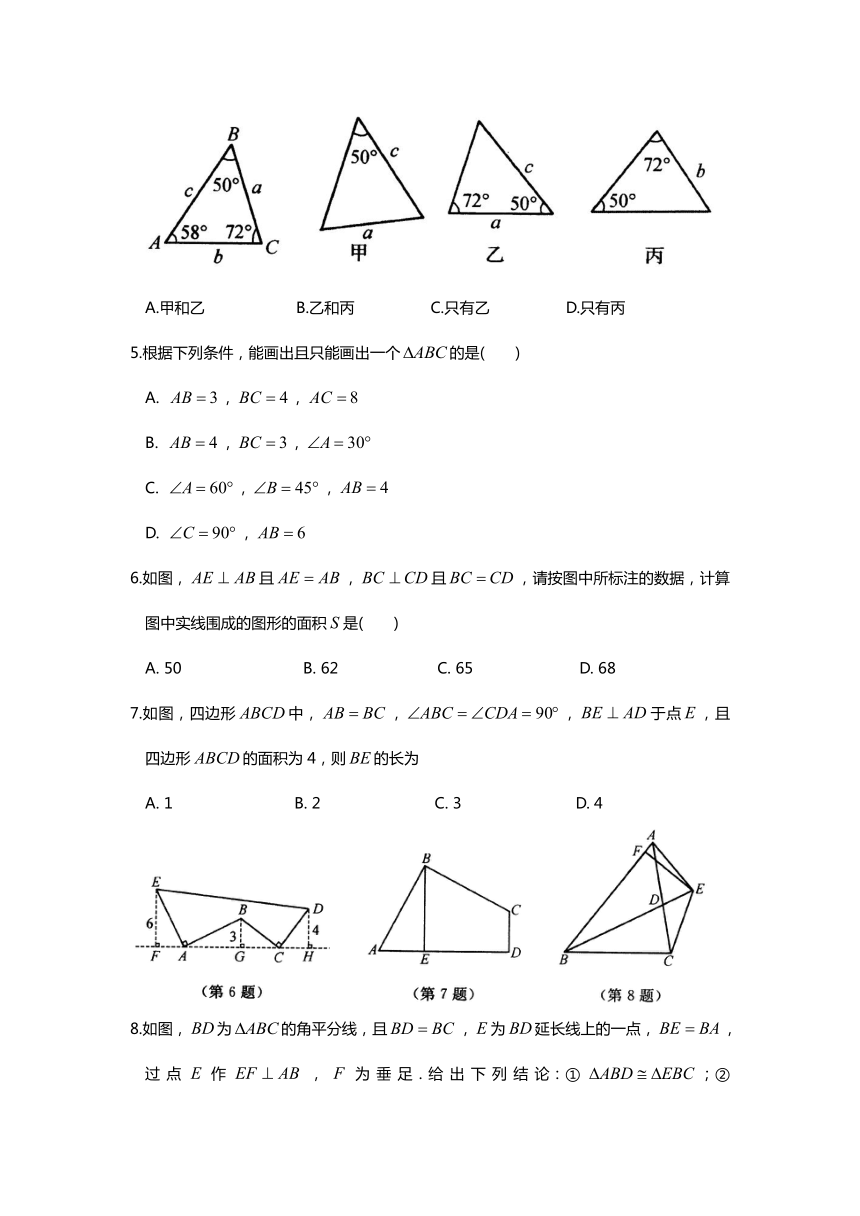
4.已知的三个内角、三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
5.根据下列条件,能画出且只能画出一个的是(
)
A.
,,
B.
,,
C.
,,
D.
,
6.如图,且,且,请按图中所标注的数据,计算图中实线围成的图形的面积是(
)
A.
50
B.
62
C.
65
D.
68
7.如图,四边形中,,,于点,且四边形的面积为4,则的长为
A.
1
B.
2
C.
3
D.
4
8.如图,为的角平分线,且,为延长线上的一点,,过点作,为垂足.给出下列结论:①;②;③;④.其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.①②③④
二、填空题(每题2分,共20分)
9.如图,一块三角形的玻璃,不小心掉在地上摔成三块,现要到玻璃店重新换一块与原来形状、大小一样的玻璃,只需带第
块到玻璃店去,理由如下:
(用文字语言说明).
10.如图,,,添加一个条件:
,使得.
11.如图,在中,是边的垂直平分线,垂足为,交于点.若,,则的周长为
.
12.如图,点在上,于点,交于点,,.若,则的度数为
.
13.如图,在中,为边的中点,,过点作直线交于点,交于点.若cm,cm,则
cm.
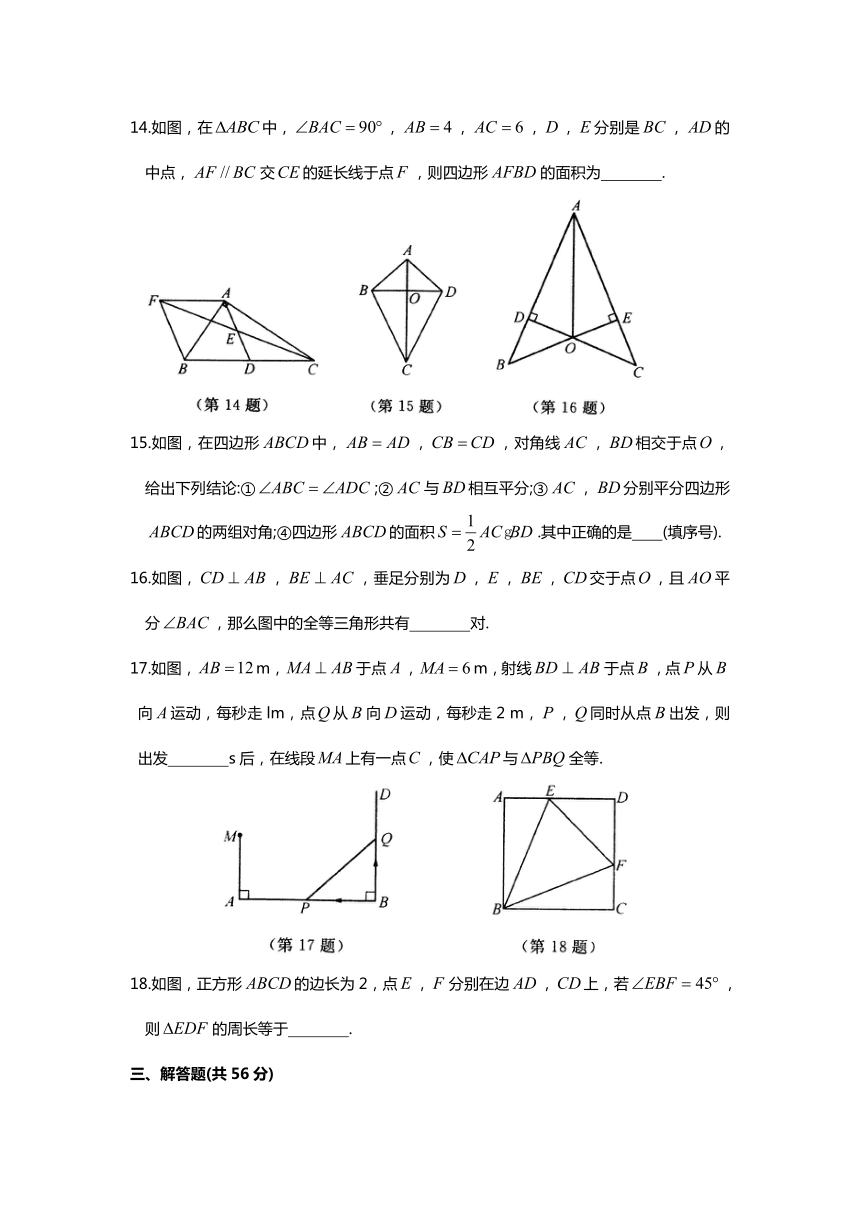
14.如图,在中,,,,,分别是,的中点,交的延长线于点,则四边形的面积为
.
15.如图,在四边形中,,,对角线,相交于点,给出下列结论:①;②与相互平分;③,分别平分四边形的两组对角;④四边形的面积.其中正确的是
(填序号).
16.如图,,,垂足分别为,,,交于点,且平分,那么图中的全等三角形共有
对.
17.如图,m,于点,m,射线于点,点从
向运动,每秒走lm,点从向运动,每秒走2
m,,同时从点出发,则出发
s后,在线段上有一点,使与全等.
18.如图,正方形的边长为2,点,分别在边,上,若,则的周长等于
.
三、解答题(共56分)
19.
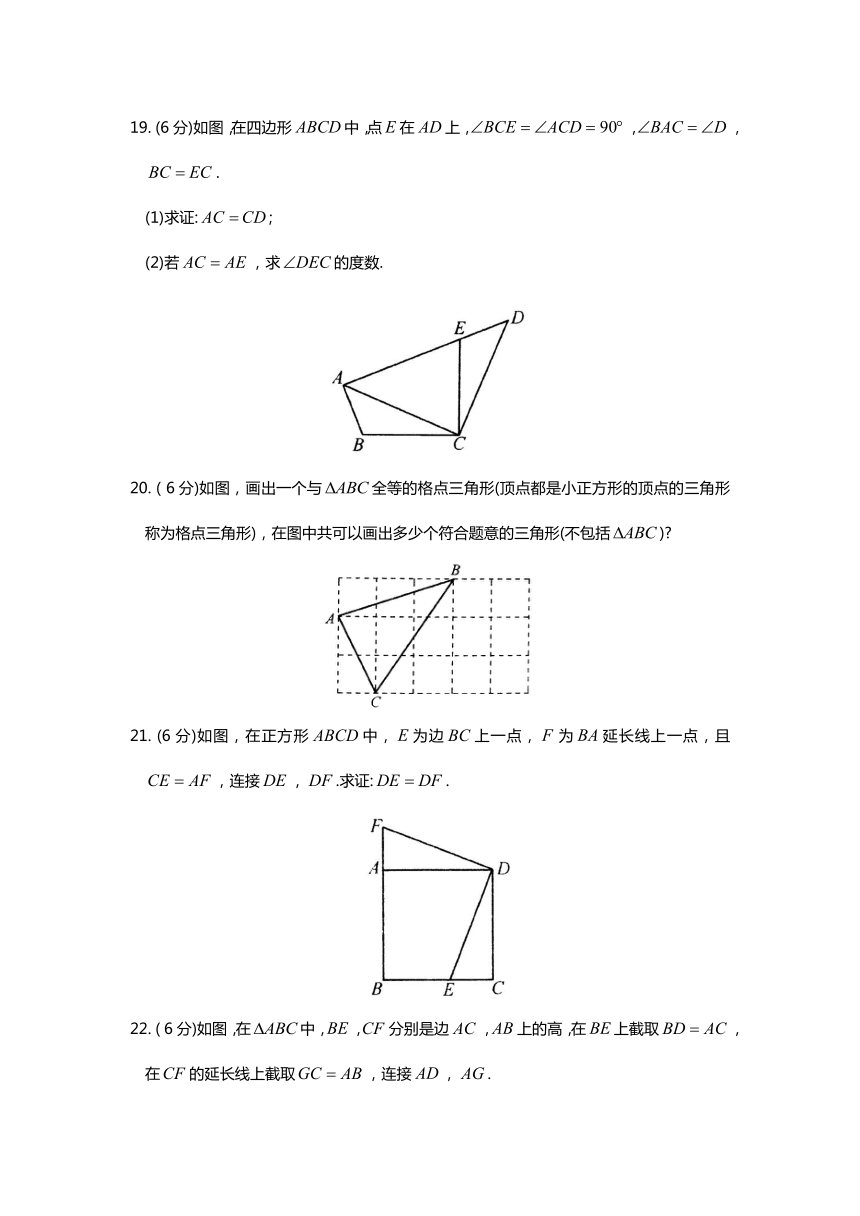
(6分)如图,在四边形中,点在上,,,.
(1)求证:;
(2)若,求的度数.
20.
(
6分)如图,画出一个与全等的格点三角形(顶点都是小正方形的顶点的三角形称为格点三角形),在图中共可以画出多少个符合题意的三角形(不包括)?
21.
(6分)如图,在正方形中,为边上一点,为延长线上一点,且,连接,.求证:.
22.
(
6分)如图,在中,,分别是边,上的高,在上截取,在的延长线上截取,连接,.
(1)求证:;
(2)
与的位置关系如何?请说明理由.
23.
(
8分)如图,点为直线上的一点.,为直线外两点,过,两点分别作直线
的垂线,垂足为,,连接,,且交直线于点,若,.求证:
(1)
;
(2)
.
24.
(8分)已知一个三角形的两条边长分别是1
cm和2
cm,一个内角为40?.
(1)请你借助图示画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图示的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由;
(3)如果将题设条件改为“三角形的两条边长分别是3
cm和4
cm,一个内角为40?”,那么满足这一条件,且彼此不全等的三角形共有
个.
(请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹)
25.
(
8分)如图,在中,cm,cm,为边的中点.
(1)如果点在线段上以3
cm/s的速度由点向点运动,同时,点在线段C上由点向点运动.
①若点的运动速度与点的运动速度相同,经过1
s后,与是否全等?请说明理由;
②若点的运动速度与点的运动速度不相等,当点的运动速度为多少时,能够使与全等?
(2)若点以②中的运动速度从点出发,点以原来的运动速度从点同时出发,都逆时针沿三边运动,则经过多长时间,点与点第一次在的哪条边上相遇?
26.
(
8分)
(1)如图①,在四边形中,,,,分别是边,上的点,且.求证:
.
(2)如图②,在四边形中,,,,分别是边,上的点,且,(1)中的结论是否仍然成立?
(3)如图③,在四边形中,,,,分别是边,延长线上的点,且,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
参考答案
1-8
BCBBCABD
9.
③
两角和它们所夹的边可以确定一个三角形
10.
,答案不唯一
11.
15
12.
55?
13.
10
14.
12
15.
①④
16.
4
17.
4
18.
4
19.
(1)
(2)
20.
结合图形可得共有23个符合题意的三角形
21.
提示:
22.
(1)提示:
(2)
23.
(1)提示:
(2)
24.
(1)
如图①所示,(2)
如图②所示
(3)4
25.
(1)
①全等
②cm/s
(2)
点与点第一次在边上相遇
26.
(1)
提示:
,
(2)
成立
(3)
,不成立,应是
(4)
(考试时间:90分钟
满分:100分)
一、选择题(每题3分,共24分)
1.如图,于点,于点,平分,则的理由是(
)
A.
SAS
B.
AAS
C.
SSS
D.
HL
2.如图,,,,下列条件中,不能判断的是(
)
A.
B.
C.
D.
3.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是(
)
A.
15
B.
30
C.
45
D.
60
4.已知的三个内角、三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
5.根据下列条件,能画出且只能画出一个的是(
)
A.
,,
B.
,,
C.
,,
D.
,
6.如图,且,且,请按图中所标注的数据,计算图中实线围成的图形的面积是(
)
A.
50
B.
62
C.
65
D.
68
7.如图,四边形中,,,于点,且四边形的面积为4,则的长为
A.
1
B.
2
C.
3
D.
4
8.如图,为的角平分线,且,为延长线上的一点,,过点作,为垂足.给出下列结论:①;②;③;④.其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.①②③④
二、填空题(每题2分,共20分)
9.如图,一块三角形的玻璃,不小心掉在地上摔成三块,现要到玻璃店重新换一块与原来形状、大小一样的玻璃,只需带第
块到玻璃店去,理由如下:
(用文字语言说明).
10.如图,,,添加一个条件:
,使得.
11.如图,在中,是边的垂直平分线,垂足为,交于点.若,,则的周长为
.
12.如图,点在上,于点,交于点,,.若,则的度数为
.
13.如图,在中,为边的中点,,过点作直线交于点,交于点.若cm,cm,则
cm.
14.如图,在中,,,,,分别是,的中点,交的延长线于点,则四边形的面积为
.
15.如图,在四边形中,,,对角线,相交于点,给出下列结论:①;②与相互平分;③,分别平分四边形的两组对角;④四边形的面积.其中正确的是
(填序号).
16.如图,,,垂足分别为,,,交于点,且平分,那么图中的全等三角形共有
对.
17.如图,m,于点,m,射线于点,点从
向运动,每秒走lm,点从向运动,每秒走2
m,,同时从点出发,则出发
s后,在线段上有一点,使与全等.
18.如图,正方形的边长为2,点,分别在边,上,若,则的周长等于
.
三、解答题(共56分)
19.
(6分)如图,在四边形中,点在上,,,.
(1)求证:;
(2)若,求的度数.
20.
(
6分)如图,画出一个与全等的格点三角形(顶点都是小正方形的顶点的三角形称为格点三角形),在图中共可以画出多少个符合题意的三角形(不包括)?
21.
(6分)如图,在正方形中,为边上一点,为延长线上一点,且,连接,.求证:.
22.
(
6分)如图,在中,,分别是边,上的高,在上截取,在的延长线上截取,连接,.
(1)求证:;
(2)
与的位置关系如何?请说明理由.
23.
(
8分)如图,点为直线上的一点.,为直线外两点,过,两点分别作直线
的垂线,垂足为,,连接,,且交直线于点,若,.求证:
(1)
;
(2)
.
24.
(8分)已知一个三角形的两条边长分别是1
cm和2
cm,一个内角为40?.
(1)请你借助图示画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图示的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由;
(3)如果将题设条件改为“三角形的两条边长分别是3
cm和4
cm,一个内角为40?”,那么满足这一条件,且彼此不全等的三角形共有
个.
(请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹)
25.
(
8分)如图,在中,cm,cm,为边的中点.
(1)如果点在线段上以3
cm/s的速度由点向点运动,同时,点在线段C上由点向点运动.
①若点的运动速度与点的运动速度相同,经过1
s后,与是否全等?请说明理由;
②若点的运动速度与点的运动速度不相等,当点的运动速度为多少时,能够使与全等?
(2)若点以②中的运动速度从点出发,点以原来的运动速度从点同时出发,都逆时针沿三边运动,则经过多长时间,点与点第一次在的哪条边上相遇?
26.
(
8分)
(1)如图①,在四边形中,,,,分别是边,上的点,且.求证:
.
(2)如图②,在四边形中,,,,分别是边,上的点,且,(1)中的结论是否仍然成立?
(3)如图③,在四边形中,,,,分别是边,延长线上的点,且,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
参考答案
1-8
BCBBCABD
9.
③
两角和它们所夹的边可以确定一个三角形
10.
,答案不唯一
11.
15
12.
55?
13.
10
14.
12
15.
①④
16.
4
17.
4
18.
4
19.
(1)
(2)
20.
结合图形可得共有23个符合题意的三角形
21.
提示:
22.
(1)提示:
(2)
23.
(1)提示:
(2)
24.
(1)
如图①所示,(2)
如图②所示
(3)4
25.
(1)
①全等
②cm/s
(2)
点与点第一次在边上相遇
26.
(1)
提示:
,
(2)
成立
(3)
,不成立,应是
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
