冀教版九年级数学上册23.4用样本估计总体课件(共21张PPT)
文档属性
| 名称 | 冀教版九年级数学上册23.4用样本估计总体课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 09:45:01 | ||
图片预览








文档简介
(共21张PPT)
23.4用样本估计总体
冀教版九上
第二十三章
数据分析
新课引入
新课学习
典例精析
测试小结
01
知道抽样调查应用的广泛性,体会样本和总体的关系.
03
会用样本平均数(方差)去估计总体平均数(方差).
02
认识当样本容量较大时,样本平均数(方差)具有稳定的规律.
学习目标
冀教版九上
情景一.“鱼塘问题”小明与客户签订销售合同,需要了解自己鱼塘里鱼的数量,请你帮小明设计一个合理的方案.
新课引入
这个方案体现了什么样的统计思想?
③用②中做标记的鱼所占的比例(5%)去估计整个鱼塘做标记的鱼所占的比例(也是5%);
②过一段时间后,又捞出200条鱼,查看做标记的鱼有几条,(比如有10条);
①从鱼塘捞出100条鱼做好标记后放回鱼塘;
④从而计算出鱼塘里鱼的数量.(100÷5%=2000)
用样本估计总体
一个样本
用样本中比例估计总体中的比例
情景一.“鱼塘问题”小明与客户签订销售合同,需要了解自己鱼塘里鱼的数量,请你帮小明设计一个合理的方案.
新课引入
你还知道哪些与此类似的问题?
例如:估计不透明袋子中球的数目
估计树林中鸟的数目等等
情景二.为了估计全校初中女生的平均身高,九年级(一)班的8个课外学习小组采用随机抽样方法,分别抽取容量为25和100的样本,样本平均数用
和
表示,结果如下:
新课引入
(1)对容量相同的不同样本,算得的样本平均数相同吗?说明了什么?
158.5
160.5
1
小组序号
161.5
159.0
160.2
160.5
160.0
159.3
160.9
159.8
160.4
161.0
159.0
159.6
159.5
160.8
2
3
4
5
6
7
8
容量相同的不同样本,样本平均数一般不相同.
样本平均数具有不确定性.
(2)把得到的样本平均数标在数轴上,观察数轴,在两组样本平均数中,哪一组样本平均数的波动小?这说明了什么?
新课引入
容量为100的样本平均数波动较小,这说明了随样本容量的增加,样本平均数呈现一种稳定性的规律.
●
●
●
●
●
●
●
●
160.0
160.4
160.9
161.5
160.2
159.5
159.0
158.5
●
●
●
●
●
●
●
●
160.0
160.5
160.8
159.8
161.0
159.6
159.3
159.0
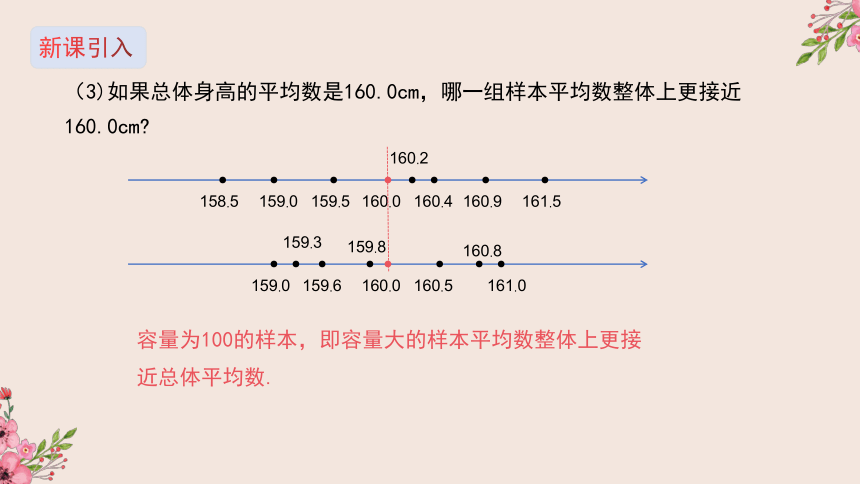
(3)如果总体身高的平均数是160.0cm,哪一组样本平均数整体上更接近160.0cm?
新课引入
容量为100的样本,即容量大的样本平均数整体上更接近总体平均数.
●
●
●
●
●
●
●
●
160.0
160.4
160.9
161.5
160.2
159.5
159.0
158.5
●
●
●
●
●
●
●
●
160.0
160.5
160.8
159.8
161.0
159.6
159.3
159.0
总结
一、样本与总体的关系
由于样本的随机性,即使是相同的样本容量,不同样本的平均数一般也不相同;当样本容量较小时,差异比较大,当样本容量增大时,样本平均数的波动小,逐渐稳定在总体平均数的附近.
因此在实际中常用样本平均数估计总体平均数.
同样的道理,也可以用样本的方差估计总体的方差.
抽取样本要具有代表性,才能保证估计的结果可信、可靠.
典例精析
例1:为了估计“情景一”中小明家鱼塘鱼的总重量.从鱼塘中任意捞出6条鱼,称得重量如下(单位:kg):
请你估计小明家鱼塘中鱼的总重量?
解:6条鱼的平均重量为
(2+1.5+1.6+1.7+2+1.4)÷6=1.7(kg)
用样本平均数估计总体平均数,鱼塘中每条鱼的平均重量为1.7kg
∴小明家鱼塘中鱼的总重量为
1.7×2000=3400(kg)
2
1.5
1.6
1.7
2
1.4
用样本平均数估计总体平均数
典例精析
例2.工人师傅用车床加工一种直径为20mm的轴,从某天加工的轴中随机抽取了10件,测得其直径(单位:mm)如下:
20.1
19.0
20.3
20.2
19.8
19.7
19.9
20.3
20.0
19.8
若规定当方差不超过0.05m㎡时,车床生产情况为正常,判断这台车床的生产情况是否正常.
分析:我们需要根据总体方差的数据来判断车床生产情况是否正常,
题中给出了样本的数据,我们就需要计算样本平均数及方差,
用样本估计总体,从而得到总体的方差数据,进而做出判断.
典例精析
用样本估计总体,可得总体方差为0.042
0.042<0.05
∴这台车床的生产情况正常.
用样本方差估计总体方差
典例精析
例3.某地区为筹备召开中学生运动会,指定要从某校九年级9个班中抽取48名女生组成花束队,要求队员的身高一致,现随机抽取10名九年级某班女生体检表(各班女生人数均超过20人),身高如下(单位:厘米):
165
162
158
157
162
162
154
160
167
155
问该校能否按要求组成花束队,试说明理由.
解:由于样本的众数为162厘米,即10人中有3人身高为162cm,从而可估计一个班级至少有6名女同学的身高为162厘米.进而可估计全校身高为162厘米的女生数为:6×9=54>48。所以该校能按要求组成花束队。
用样本中的比例估计总体中的比例
巩固练习
1.从总体中抽取一部分数据作为样本去估计总体.下面叙述正确的是(
)
A.样本容量越大,样本平均数就越大.
B.样本容量越大,样本方差就越大.
C.样本容量越大,样本方差就越小.
D.样本容量越大,对总体的估计就越准确.
D
巩固练习
2.某地举行了一次数学竞赛,为了估计平均成绩,在抽取的部分试卷中,有1人得10分,3人得9分,8人得8分,12人得7分,9人得6分,7分得5分,则样本容量(
),样本平均数是(
).由此估计这次数学竞赛的平均成绩是(
).
40
6.85分
6.85分
巩固练习
3.为比较甲、乙两组电子钟每日走时误差情况,从这两种电子钟中,个随机抽取10台进行测试.测试结果是两组电子钟的走时误差的平均数相同,方差分别是
则走时比较稳定的是(
)
乙
巩固练习
4.估计鱼塘里鱼的数量时,先从鱼塘中捞出200条鱼做上标记再放回鱼塘,经过一段时间后有捞出300条,发现有标记的鱼有20条,则,鱼塘里鱼的数量大约(
)条.
3000
巩固练习
5.一个果园有1000课树龄相同的苹果树.任意选择了5课苹果树,数出它们挂果是数量分别为260,340,280,420,360.根据去年的经验,平均每个苹果的重量约为250g,批发价为4元/kg,则估计今年果园的收入约是(
)元.
332000
巩固练习
6.已知共享某共享单车的收费标准为:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比商场车费减少0.1元,第6次开始,当次用车免费.收费如下表:
使用次数
0
1
2
3
4
5(含5次以上)
累计车费
0
0.5
0.9
1.2
1.4
1.5
就此收费方案随机调查了某高校100名师生在一天中使用此品牌共享单车的意愿,得到数据如下:
使用次数
0
1
2
3
4
5(含5次以上)
人数
5
15
10
30
25
15
若此共享单车投放该校一天的费用为5800元,而该校师生共5000人,问共享单车运营商能否盈利?
巩固练习
解:抽取的100名师生每人每天使用共享单车的平均费用为
(0×5+0.5×15+0.9×10+1.2×30+1.4×25+1.5×15)÷10=1.1(元)
用样本估计总体,可得5000名师生每人每天的平均费用约1.1元.
1.1×5000=5500
5500<5800
∴共享单车运营商不能盈利.
回顾小结
2.当样本容量较大时,样本的统计量就会具有稳定性的规律.
3.比较常用的是用样本平均数估计总体平均数,用样本方差估计总体方差.
1.统计的核心思想是由样本推断总体.由于是样本的统计量去估计总体的统计量,为使结果准确,我们需要尽量使样本具有代表性.
同学们再见
23.4用样本估计总体
冀教版九上
第二十三章
数据分析
新课引入
新课学习
典例精析
测试小结
01
知道抽样调查应用的广泛性,体会样本和总体的关系.
03
会用样本平均数(方差)去估计总体平均数(方差).
02
认识当样本容量较大时,样本平均数(方差)具有稳定的规律.
学习目标
冀教版九上
情景一.“鱼塘问题”小明与客户签订销售合同,需要了解自己鱼塘里鱼的数量,请你帮小明设计一个合理的方案.
新课引入
这个方案体现了什么样的统计思想?
③用②中做标记的鱼所占的比例(5%)去估计整个鱼塘做标记的鱼所占的比例(也是5%);
②过一段时间后,又捞出200条鱼,查看做标记的鱼有几条,(比如有10条);
①从鱼塘捞出100条鱼做好标记后放回鱼塘;
④从而计算出鱼塘里鱼的数量.(100÷5%=2000)
用样本估计总体
一个样本
用样本中比例估计总体中的比例
情景一.“鱼塘问题”小明与客户签订销售合同,需要了解自己鱼塘里鱼的数量,请你帮小明设计一个合理的方案.
新课引入
你还知道哪些与此类似的问题?
例如:估计不透明袋子中球的数目
估计树林中鸟的数目等等
情景二.为了估计全校初中女生的平均身高,九年级(一)班的8个课外学习小组采用随机抽样方法,分别抽取容量为25和100的样本,样本平均数用
和
表示,结果如下:
新课引入
(1)对容量相同的不同样本,算得的样本平均数相同吗?说明了什么?
158.5
160.5
1
小组序号
161.5
159.0
160.2
160.5
160.0
159.3
160.9
159.8
160.4
161.0
159.0
159.6
159.5
160.8
2
3
4
5
6
7
8
容量相同的不同样本,样本平均数一般不相同.
样本平均数具有不确定性.
(2)把得到的样本平均数标在数轴上,观察数轴,在两组样本平均数中,哪一组样本平均数的波动小?这说明了什么?
新课引入
容量为100的样本平均数波动较小,这说明了随样本容量的增加,样本平均数呈现一种稳定性的规律.
●
●
●
●
●
●
●
●
160.0
160.4
160.9
161.5
160.2
159.5
159.0
158.5
●
●
●
●
●
●
●
●
160.0
160.5
160.8
159.8
161.0
159.6
159.3
159.0
(3)如果总体身高的平均数是160.0cm,哪一组样本平均数整体上更接近160.0cm?
新课引入
容量为100的样本,即容量大的样本平均数整体上更接近总体平均数.
●
●
●
●
●
●
●
●
160.0
160.4
160.9
161.5
160.2
159.5
159.0
158.5
●
●
●
●
●
●
●
●
160.0
160.5
160.8
159.8
161.0
159.6
159.3
159.0
总结
一、样本与总体的关系
由于样本的随机性,即使是相同的样本容量,不同样本的平均数一般也不相同;当样本容量较小时,差异比较大,当样本容量增大时,样本平均数的波动小,逐渐稳定在总体平均数的附近.
因此在实际中常用样本平均数估计总体平均数.
同样的道理,也可以用样本的方差估计总体的方差.
抽取样本要具有代表性,才能保证估计的结果可信、可靠.
典例精析
例1:为了估计“情景一”中小明家鱼塘鱼的总重量.从鱼塘中任意捞出6条鱼,称得重量如下(单位:kg):
请你估计小明家鱼塘中鱼的总重量?
解:6条鱼的平均重量为
(2+1.5+1.6+1.7+2+1.4)÷6=1.7(kg)
用样本平均数估计总体平均数,鱼塘中每条鱼的平均重量为1.7kg
∴小明家鱼塘中鱼的总重量为
1.7×2000=3400(kg)
2
1.5
1.6
1.7
2
1.4
用样本平均数估计总体平均数
典例精析
例2.工人师傅用车床加工一种直径为20mm的轴,从某天加工的轴中随机抽取了10件,测得其直径(单位:mm)如下:
20.1
19.0
20.3
20.2
19.8
19.7
19.9
20.3
20.0
19.8
若规定当方差不超过0.05m㎡时,车床生产情况为正常,判断这台车床的生产情况是否正常.
分析:我们需要根据总体方差的数据来判断车床生产情况是否正常,
题中给出了样本的数据,我们就需要计算样本平均数及方差,
用样本估计总体,从而得到总体的方差数据,进而做出判断.
典例精析
用样本估计总体,可得总体方差为0.042
0.042<0.05
∴这台车床的生产情况正常.
用样本方差估计总体方差
典例精析
例3.某地区为筹备召开中学生运动会,指定要从某校九年级9个班中抽取48名女生组成花束队,要求队员的身高一致,现随机抽取10名九年级某班女生体检表(各班女生人数均超过20人),身高如下(单位:厘米):
165
162
158
157
162
162
154
160
167
155
问该校能否按要求组成花束队,试说明理由.
解:由于样本的众数为162厘米,即10人中有3人身高为162cm,从而可估计一个班级至少有6名女同学的身高为162厘米.进而可估计全校身高为162厘米的女生数为:6×9=54>48。所以该校能按要求组成花束队。
用样本中的比例估计总体中的比例
巩固练习
1.从总体中抽取一部分数据作为样本去估计总体.下面叙述正确的是(
)
A.样本容量越大,样本平均数就越大.
B.样本容量越大,样本方差就越大.
C.样本容量越大,样本方差就越小.
D.样本容量越大,对总体的估计就越准确.
D
巩固练习
2.某地举行了一次数学竞赛,为了估计平均成绩,在抽取的部分试卷中,有1人得10分,3人得9分,8人得8分,12人得7分,9人得6分,7分得5分,则样本容量(
),样本平均数是(
).由此估计这次数学竞赛的平均成绩是(
).
40
6.85分
6.85分
巩固练习
3.为比较甲、乙两组电子钟每日走时误差情况,从这两种电子钟中,个随机抽取10台进行测试.测试结果是两组电子钟的走时误差的平均数相同,方差分别是
则走时比较稳定的是(
)
乙
巩固练习
4.估计鱼塘里鱼的数量时,先从鱼塘中捞出200条鱼做上标记再放回鱼塘,经过一段时间后有捞出300条,发现有标记的鱼有20条,则,鱼塘里鱼的数量大约(
)条.
3000
巩固练习
5.一个果园有1000课树龄相同的苹果树.任意选择了5课苹果树,数出它们挂果是数量分别为260,340,280,420,360.根据去年的经验,平均每个苹果的重量约为250g,批发价为4元/kg,则估计今年果园的收入约是(
)元.
332000
巩固练习
6.已知共享某共享单车的收费标准为:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比商场车费减少0.1元,第6次开始,当次用车免费.收费如下表:
使用次数
0
1
2
3
4
5(含5次以上)
累计车费
0
0.5
0.9
1.2
1.4
1.5
就此收费方案随机调查了某高校100名师生在一天中使用此品牌共享单车的意愿,得到数据如下:
使用次数
0
1
2
3
4
5(含5次以上)
人数
5
15
10
30
25
15
若此共享单车投放该校一天的费用为5800元,而该校师生共5000人,问共享单车运营商能否盈利?
巩固练习
解:抽取的100名师生每人每天使用共享单车的平均费用为
(0×5+0.5×15+0.9×10+1.2×30+1.4×25+1.5×15)÷10=1.1(元)
用样本估计总体,可得5000名师生每人每天的平均费用约1.1元.
1.1×5000=5500
5500<5800
∴共享单车运营商不能盈利.
回顾小结
2.当样本容量较大时,样本的统计量就会具有稳定性的规律.
3.比较常用的是用样本平均数估计总体平均数,用样本方差估计总体方差.
1.统计的核心思想是由样本推断总体.由于是样本的统计量去估计总体的统计量,为使结果准确,我们需要尽量使样本具有代表性.
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
