沪教版(上海)八年级上册 19.7 直角三角形全等的判定 同步习题 (word 版 含答案)
文档属性
| 名称 | 沪教版(上海)八年级上册 19.7 直角三角形全等的判定 同步习题 (word 版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 00:00:00 | ||
图片预览


文档简介
19.7
直角三角形全等的判定
同步习题
一、选择题
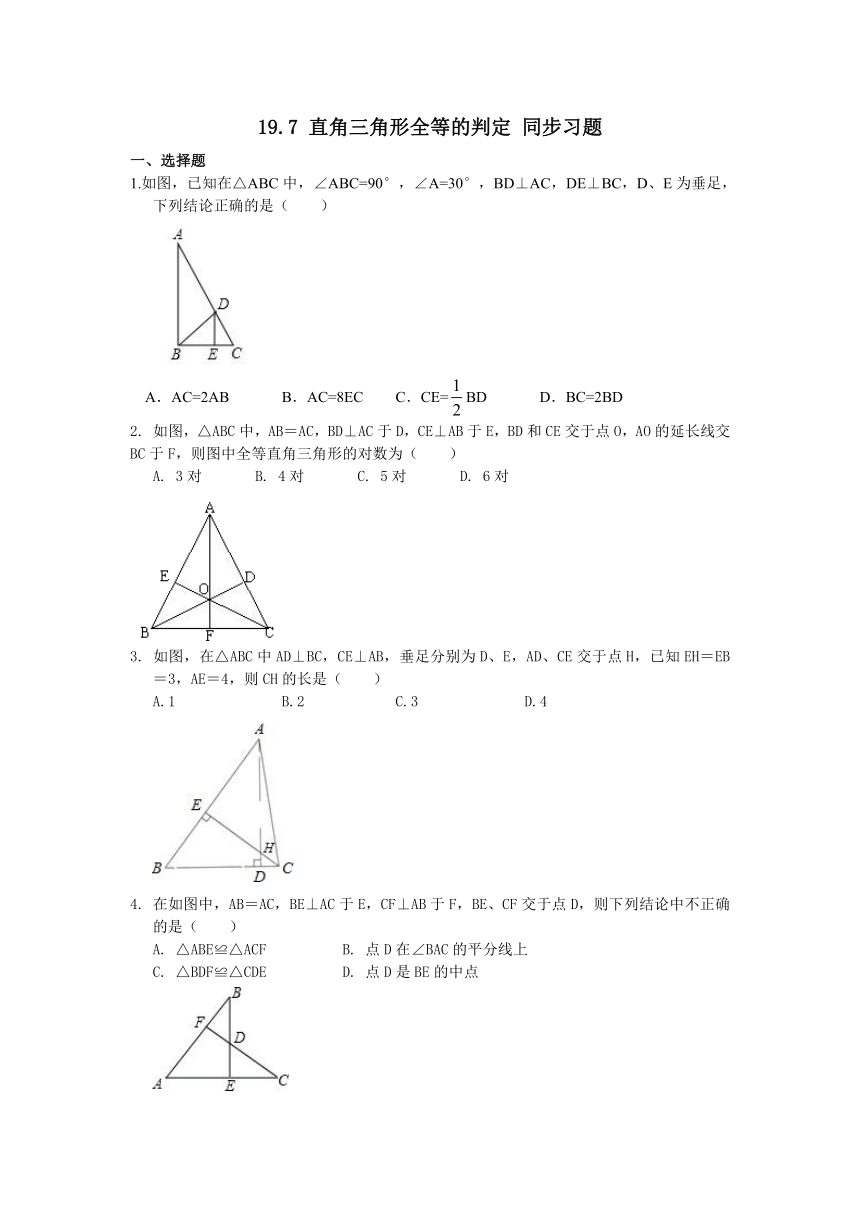
1.如图,已知在△ABC中,∠ABC=90°,∠A=30°,BD⊥AC,DE⊥BC,D、E为垂足,下列结论正确的是( )
A.AC=2AB
B.AC=8EC
C.CE=BD
D.BC=2BD
2.
如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于点O,AO的延长线交BC于F,则图中全等直角三角形的对数为(
)
A.
3对
B.
4对
C.
5对
D.
6对
3.
如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A.1
B.2
C.3
D.4
4.
在如图中,AB=AC,BE⊥AC于E,CF⊥AB于F,BE、CF交于点D,则下列结论中不正确的是( )
A.
△ABE≌△ACF
B.
点D在∠BAC的平分线上
C.
△BDF≌△CDE
D.
点D是BE的中点
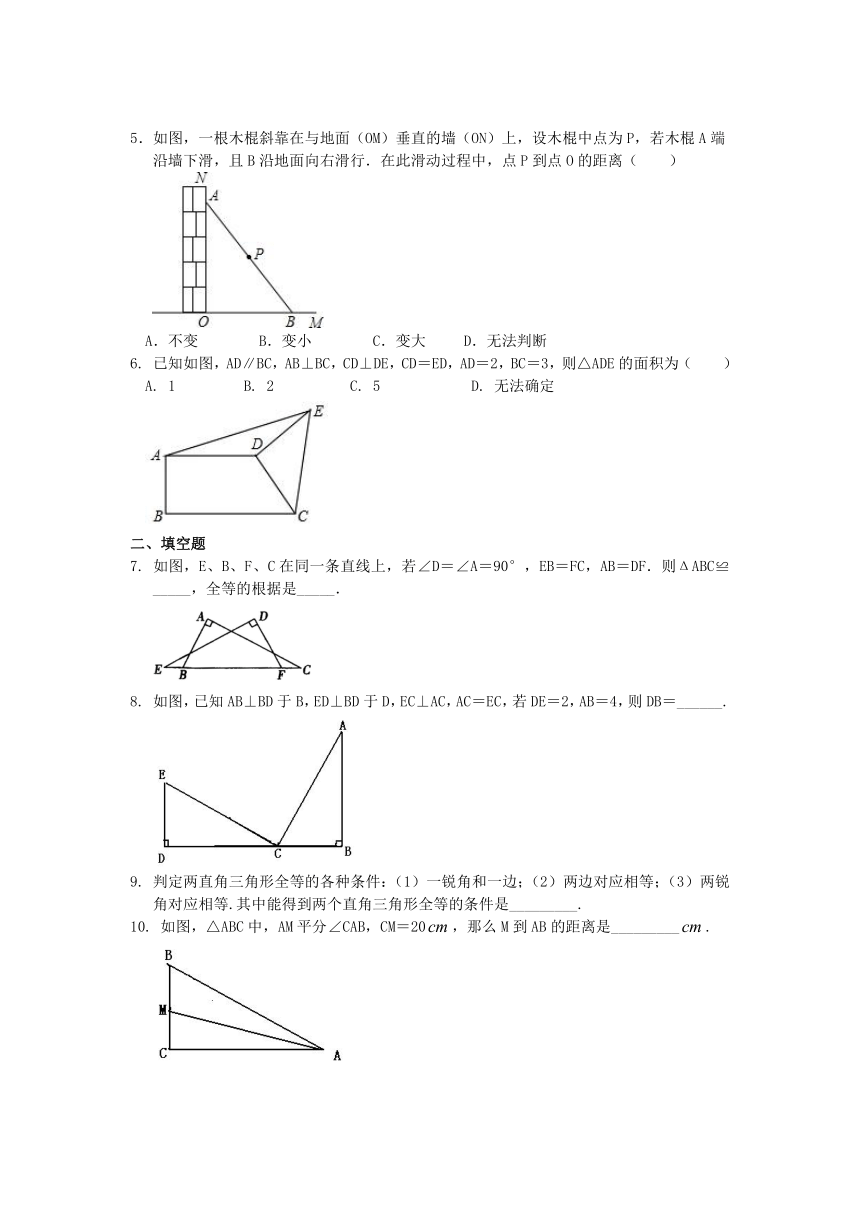
5.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.不变
B.变小
C.变大
D.无法判断
6.
已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.
1
B.
2
C.
5
D.
无法确定
二、填空题
7.
如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌_____,全等的根据是_____.
8.
如图,已知AB⊥BD于B,ED⊥BD于D,EC⊥AC,AC=EC,若DE=2,AB=4,则DB=______.
9.
判定两直角三角形全等的各种条件:(1)一锐角和一边;(2)两边对应相等;(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是_________.
10.
如图,△ABC中,AM平分∠CAB,CM=20,那么M到AB的距离是_________.
11.
如图,已知AD是△ABC的高,E为AC上一点,BE交AD于F,且BF=AC,FD=CD.则
∠BAD=_______.
12.如图,已知△ABC中,AB=AC=8cm,AD平分∠BAC,点E为AC的中点,则DE=
.
三、解答题
13.
如图所示,在△ABC中,AB=AC,D是BC边上的点,DE⊥AB,DF⊥AC,垂足分别为点E、F,∠BAC=120°.
求证:.
14.如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;
(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
15.
如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF.
参考答案
一.选择题
1.
B;
2.
D;
3.
A;
4.
D;
5.
A;
6.
A;
二.填空题
7.
△DFE,HL;
8.
6;
9.
(1)(2)
10.20;
11.45°;
12.4cm;
三.解答题
13.
证明:∵
在△ABC中,AB=AC,∠BAC=120°,
∴
∠B=∠C=.
∵
DE⊥AB,DF⊥AC,
∴
,.
∴
.
14.
解:(1)如图,连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点.
∴DM=BC,ME=
BC,
∴DM=ME,
又∵N是DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°-2∠ABC)+(180°-2∠ACB)
=360°-2(∠ABC+∠ACB)
=360°-2(180°-∠A)=2∠A,
∴∠DME=180°-2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:
在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC=2(180°-∠A)=360°-2∠A
∴∠DME=180°-(360°-2∠A)=2∠A-180°.
15.
证明∵DE⊥AC,BF⊥AC,∴∠DEG=∠BFE=90°.
∵AE=CF,AE+EF=CF+EF.
即AF=CE.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFG和△DEG中,
∴△BFG≌△DEG(AAS),
∴FG=EG,即BD平分EF.
PAGE
直角三角形全等的判定
同步习题
一、选择题
1.如图,已知在△ABC中,∠ABC=90°,∠A=30°,BD⊥AC,DE⊥BC,D、E为垂足,下列结论正确的是( )
A.AC=2AB
B.AC=8EC
C.CE=BD
D.BC=2BD
2.
如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于点O,AO的延长线交BC于F,则图中全等直角三角形的对数为(
)
A.
3对
B.
4对
C.
5对
D.
6对
3.
如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A.1
B.2
C.3
D.4
4.
在如图中,AB=AC,BE⊥AC于E,CF⊥AB于F,BE、CF交于点D,则下列结论中不正确的是( )
A.
△ABE≌△ACF
B.
点D在∠BAC的平分线上
C.
△BDF≌△CDE
D.
点D是BE的中点
5.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.不变
B.变小
C.变大
D.无法判断
6.
已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.
1
B.
2
C.
5
D.
无法确定
二、填空题
7.
如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌_____,全等的根据是_____.
8.
如图,已知AB⊥BD于B,ED⊥BD于D,EC⊥AC,AC=EC,若DE=2,AB=4,则DB=______.
9.
判定两直角三角形全等的各种条件:(1)一锐角和一边;(2)两边对应相等;(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是_________.
10.
如图,△ABC中,AM平分∠CAB,CM=20,那么M到AB的距离是_________.
11.
如图,已知AD是△ABC的高,E为AC上一点,BE交AD于F,且BF=AC,FD=CD.则
∠BAD=_______.
12.如图,已知△ABC中,AB=AC=8cm,AD平分∠BAC,点E为AC的中点,则DE=
.
三、解答题
13.
如图所示,在△ABC中,AB=AC,D是BC边上的点,DE⊥AB,DF⊥AC,垂足分别为点E、F,∠BAC=120°.
求证:.
14.如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;
(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
15.
如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF.
参考答案
一.选择题
1.
B;
2.
D;
3.
A;
4.
D;
5.
A;
6.
A;
二.填空题
7.
△DFE,HL;
8.
6;
9.
(1)(2)
10.20;
11.45°;
12.4cm;
三.解答题
13.
证明:∵
在△ABC中,AB=AC,∠BAC=120°,
∴
∠B=∠C=.
∵
DE⊥AB,DF⊥AC,
∴
,.
∴
.
14.
解:(1)如图,连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点.
∴DM=BC,ME=
BC,
∴DM=ME,
又∵N是DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°-2∠ABC)+(180°-2∠ACB)
=360°-2(∠ABC+∠ACB)
=360°-2(180°-∠A)=2∠A,
∴∠DME=180°-2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:
在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC=2(180°-∠A)=360°-2∠A
∴∠DME=180°-(360°-2∠A)=2∠A-180°.
15.
证明∵DE⊥AC,BF⊥AC,∴∠DEG=∠BFE=90°.
∵AE=CF,AE+EF=CF+EF.
即AF=CE.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFG和△DEG中,
∴△BFG≌△DEG(AAS),
∴FG=EG,即BD平分EF.
PAGE
