人教版八年级数学上册:11.2.2三角形的外角 课件(共27张PPT)
文档属性
| 名称 | 人教版八年级数学上册:11.2.2三角形的外角 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 350.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 03:51:20 | ||
图片预览





文档简介
(共27张PPT)
第十一章
三角形
11.2.2
三角形的外角
【学习目标】
1.掌握三角形外角的概念;
2.掌握三角形的外角的性质;
3.能利用三角形的外角性质解决实际问题。
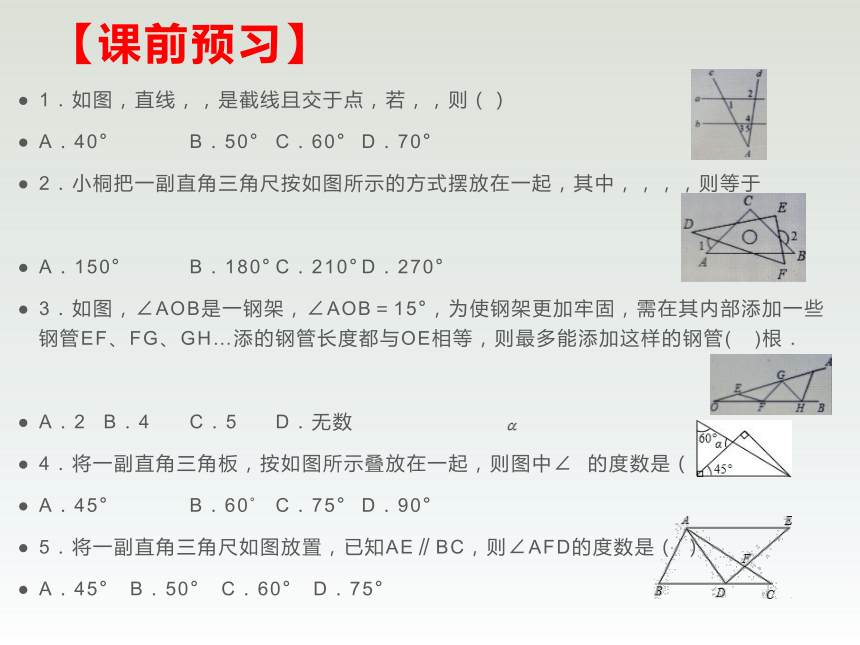
【课前预习】
1.如图,直线,,是截线且交于点,若,,则()
A.40°
B.50°
C.60°
D.70°
2.小桐把一副直角三角尺按如图所示的方式摆放在一起,其中,,,,则等于
A.150°
B.180°
C.210°
D.270°
3.如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管(
)根.
A.2
B.4
C.5
D.无数
4.将一副直角三角板,按如图所示叠放在一起,则图中∠
的度数是(
)
A.45°
B.60°
C.75°
D.90°
5.将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是(
)
A.45°
B.50°
C.60°
D.75°
【课前预习】答案
1.B
2.C
3.B
4.B
5.D
2、在ABC中,
(1)∠C=90°,∠A=30
°
,则∠B=
;
(2)∠A=50
°
,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A=
,
∠B=
,∠C=
,
40°
60°
80°
65°
60°
【学习探究】
复习回顾
三角形内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800
–(∠B+∠C).
∠B=1800
–(∠A+∠C).
∠C=1800
–(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
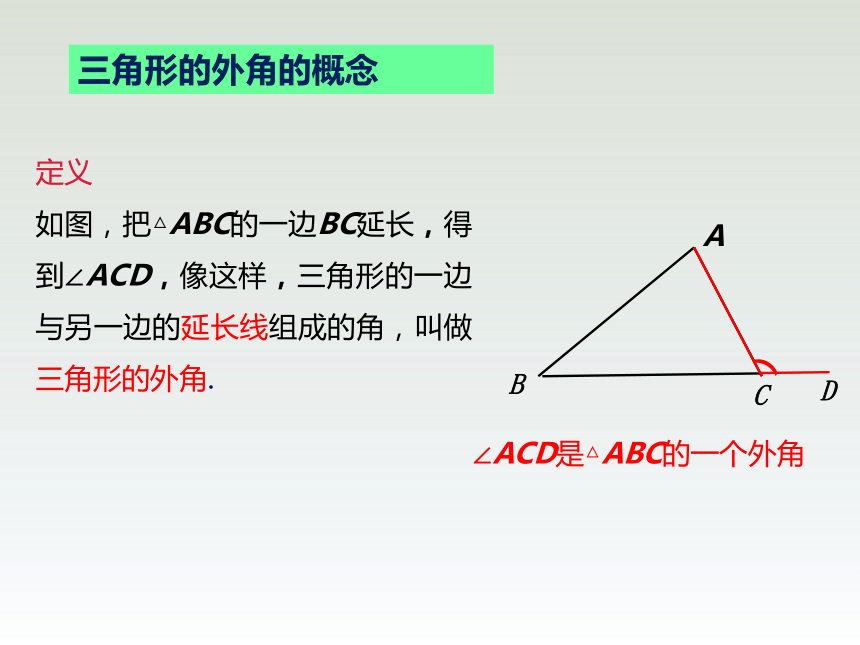
三角形的外角的概念
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
A
B
C
D
(
∠ACD是△ABC的一个外角
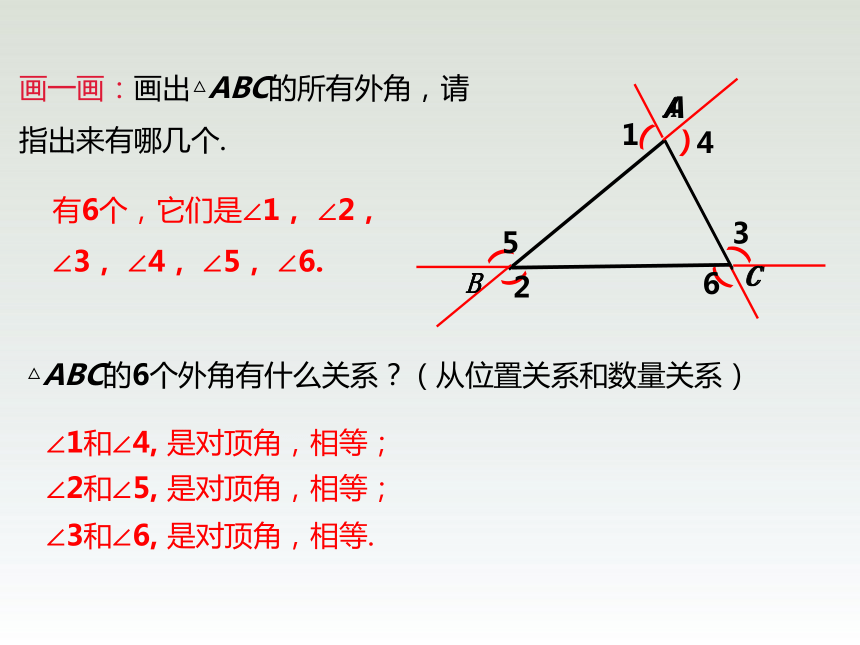
画一画:画出△ABC的所有外角,请指出来有哪几个.
△ABC的6个外角有什么关系?(从位置关系和数量关系)
(
(
(
(
(
(
A
B
C
1
2
3
4
5
6
A
B
C
有6个,它们是∠1,
∠2,
∠3,
∠4,
∠5,
∠6.
∠1和∠4,
是对顶角,相等;
∠2和∠5,
是对顶角,相等;
∠3和∠6,
是对顶角,相等.
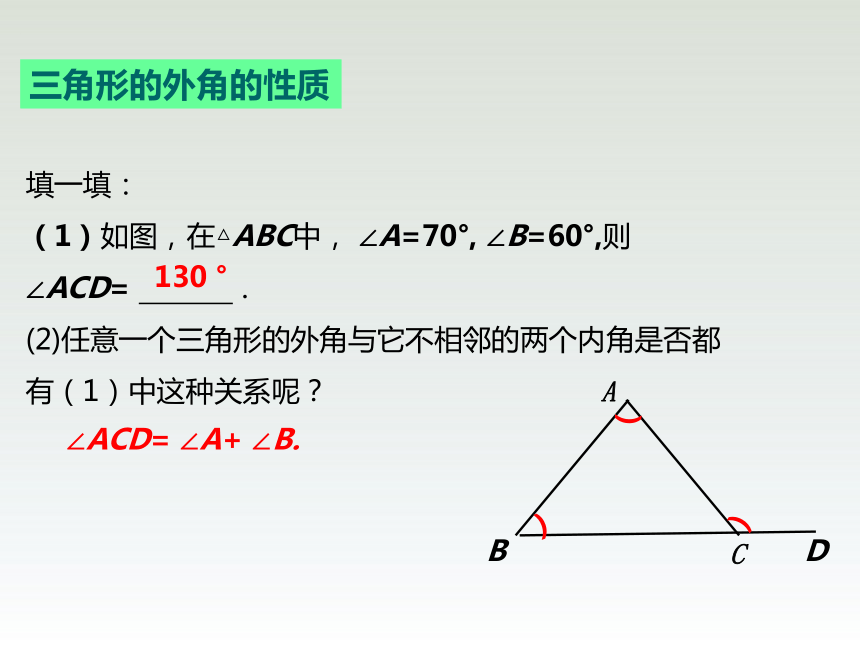
填一填:
(1)如图,在△ABC中,
∠A=70°,
∠B=60°,则∠ACD=
.
(2)任意一个三角形的外角与它不相邻的两个内角是否都有(1)中这种关系呢?
三角形的外角的性质
A
B
C
D
(
(
(
130
°
∠ACD=
∠A+
∠B.
A
B
C
D
E
看一看:
算一算:
若∠A=
55?,∠B=60?,
试求∠
ACB,
∠ACD,
∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
通过上题的计算,你发现∠ACD,
∠
CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
想一想:
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵
∠ACD是△ABC的一个外角
∴
∠ACD=
∠A+
∠B.
注意
三角形外角与内角的关系:
(1)位置关系:相邻和不相邻.
(2)数量关系:外角与相邻内角互补,
外角大于不相邻的任何一个内角.
练一练
说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80
°
60
°
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50
°
32
°
(2)
∠1=40
°,
∠2=140
°
∠1=18
°,
∠2=130
°
三角形的外角和
如图,
∠BAE,
∠CBF,
∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE=
∠2+
∠3,
∠CBF=
∠1+
∠3,
∠ACD=
∠1+
∠2.
又知∠1+
∠2+
∠3=180
°,
所以∠BAE+
∠CBF+
∠ACD
=2(∠1+
∠2+
∠3)=360
°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
你还有其他解法吗?
方法二:如图,∠BAE+∠1=180
°
①
,
∠CBF
+∠2=180
°
②,
∠ACD
+∠3=180
°
③,
又知∠1+
∠2+
∠3=180
°,
①+
②+
③得
∠BAE+
∠CBF+
∠ACD
+(∠1+
∠2+
∠3)=540
°,
所以∠BAE+
∠CBF+
∠ACD=540
°-180°=360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
三角形的外角和等于360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
∠BAE+
∠CBF+
∠ACD
=2(∠1+
∠2+
∠3)=360
°.
A
B
C
D
E
F
1
H
2
【例1】已知:国旗上的一个五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
【解析】设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
【例题】
∴
∠1=∠B+∠D(三角形的一个外角等于与它不相邻的两个内角的和).
∴
∠2=∠C+∠E(三角形的一个外角等于与它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和等于180°),
又∵
∠2是△EHC的一个外角(外角的定义),
∴
∠A+∠B+∠C+∠D+∠E
=180°(等式的性质).
【解析】∵∠1是△BDF的一个外角(外角的定义),
例2
(一题多解)如图,计算∠BDC.
A
B
C
D
(
(
(
51
°
20
°
30
°
A
B
D
E
A
C
D
E
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
(
51
°
20
°
30
°
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,
∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
E
)
)
1
2
)
3
)
4
A
B
C
D
(
(
(
51
°
20
°
30
°
E
)
1
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
(解法三)连接延长CD交AB于点F.(解题过程同解法二)
)
2
A
B
C
D
(
(
(
1
3
2
(
重要发现
∠BDC=
∠1+
∠2+
∠3.
例3:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
70°
40?
40?
⌒
【课后练习】
1.已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是(?
)
A.钝角
B.锐角
C.直角
D.无法确定
2.下列叙述正确的是
A.三角形的外角等于两个内角的和
B.三角形的外角大于内角
C.三角形任何两个内角的和都等于第三个角的外角
D.三角形每一个内角都只有一个外角
3.若三角形的一个外角等于和它相邻的内角,则这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.都有可能
4.下列说法正确的是(
)
A.三角形的每一个外角都大于和它相邻的一个内角
B.三角形的一个外角可以等于和它相邻的一个内角
C.三角形的外角和等于180°
D.三角形中至少有一个外角小于和它相邻的内角
5.三角形的一个外角,不大于和它相邻的内角,这个三角形一定是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.非锐角三角形
【课后练习】答案
1.B
2.C
3.B
4.B
5.D
6.B
7.D
8.B
9.A
10.D
11.30°
12.135°
13.75°
14.110°.
15.140°.
第十一章
三角形
11.2.2
三角形的外角
【学习目标】
1.掌握三角形外角的概念;
2.掌握三角形的外角的性质;
3.能利用三角形的外角性质解决实际问题。
【课前预习】
1.如图,直线,,是截线且交于点,若,,则()
A.40°
B.50°
C.60°
D.70°
2.小桐把一副直角三角尺按如图所示的方式摆放在一起,其中,,,,则等于
A.150°
B.180°
C.210°
D.270°
3.如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管(
)根.
A.2
B.4
C.5
D.无数
4.将一副直角三角板,按如图所示叠放在一起,则图中∠
的度数是(
)
A.45°
B.60°
C.75°
D.90°
5.将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是(
)
A.45°
B.50°
C.60°
D.75°
【课前预习】答案
1.B
2.C
3.B
4.B
5.D
2、在ABC中,
(1)∠C=90°,∠A=30
°
,则∠B=
;
(2)∠A=50
°
,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A=
,
∠B=
,∠C=
,
40°
60°
80°
65°
60°
【学习探究】
复习回顾
三角形内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800
–(∠B+∠C).
∠B=1800
–(∠A+∠C).
∠C=1800
–(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
三角形的外角的概念
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
A
B
C
D
(
∠ACD是△ABC的一个外角
画一画:画出△ABC的所有外角,请指出来有哪几个.
△ABC的6个外角有什么关系?(从位置关系和数量关系)
(
(
(
(
(
(
A
B
C
1
2
3
4
5
6
A
B
C
有6个,它们是∠1,
∠2,
∠3,
∠4,
∠5,
∠6.
∠1和∠4,
是对顶角,相等;
∠2和∠5,
是对顶角,相等;
∠3和∠6,
是对顶角,相等.
填一填:
(1)如图,在△ABC中,
∠A=70°,
∠B=60°,则∠ACD=
.
(2)任意一个三角形的外角与它不相邻的两个内角是否都有(1)中这种关系呢?
三角形的外角的性质
A
B
C
D
(
(
(
130
°
∠ACD=
∠A+
∠B.
A
B
C
D
E
看一看:
算一算:
若∠A=
55?,∠B=60?,
试求∠
ACB,
∠ACD,
∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
通过上题的计算,你发现∠ACD,
∠
CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
想一想:
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵
∠ACD是△ABC的一个外角
∴
∠ACD=
∠A+
∠B.
注意
三角形外角与内角的关系:
(1)位置关系:相邻和不相邻.
(2)数量关系:外角与相邻内角互补,
外角大于不相邻的任何一个内角.
练一练
说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80
°
60
°
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50
°
32
°
(2)
∠1=40
°,
∠2=140
°
∠1=18
°,
∠2=130
°
三角形的外角和
如图,
∠BAE,
∠CBF,
∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE=
∠2+
∠3,
∠CBF=
∠1+
∠3,
∠ACD=
∠1+
∠2.
又知∠1+
∠2+
∠3=180
°,
所以∠BAE+
∠CBF+
∠ACD
=2(∠1+
∠2+
∠3)=360
°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
你还有其他解法吗?
方法二:如图,∠BAE+∠1=180
°
①
,
∠CBF
+∠2=180
°
②,
∠ACD
+∠3=180
°
③,
又知∠1+
∠2+
∠3=180
°,
①+
②+
③得
∠BAE+
∠CBF+
∠ACD
+(∠1+
∠2+
∠3)=540
°,
所以∠BAE+
∠CBF+
∠ACD=540
°-180°=360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
三角形的外角和等于360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
∠BAE+
∠CBF+
∠ACD
=2(∠1+
∠2+
∠3)=360
°.
A
B
C
D
E
F
1
H
2
【例1】已知:国旗上的一个五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
【解析】设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
【例题】
∴
∠1=∠B+∠D(三角形的一个外角等于与它不相邻的两个内角的和).
∴
∠2=∠C+∠E(三角形的一个外角等于与它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和等于180°),
又∵
∠2是△EHC的一个外角(外角的定义),
∴
∠A+∠B+∠C+∠D+∠E
=180°(等式的性质).
【解析】∵∠1是△BDF的一个外角(外角的定义),
例2
(一题多解)如图,计算∠BDC.
A
B
C
D
(
(
(
51
°
20
°
30
°
A
B
D
E
A
C
D
E
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
(
51
°
20
°
30
°
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,
∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
E
)
)
1
2
)
3
)
4
A
B
C
D
(
(
(
51
°
20
°
30
°
E
)
1
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
(解法三)连接延长CD交AB于点F.(解题过程同解法二)
)
2
A
B
C
D
(
(
(
1
3
2
(
重要发现
∠BDC=
∠1+
∠2+
∠3.
例3:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
70°
40?
40?
⌒
【课后练习】
1.已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是(?
)
A.钝角
B.锐角
C.直角
D.无法确定
2.下列叙述正确的是
A.三角形的外角等于两个内角的和
B.三角形的外角大于内角
C.三角形任何两个内角的和都等于第三个角的外角
D.三角形每一个内角都只有一个外角
3.若三角形的一个外角等于和它相邻的内角,则这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.都有可能
4.下列说法正确的是(
)
A.三角形的每一个外角都大于和它相邻的一个内角
B.三角形的一个外角可以等于和它相邻的一个内角
C.三角形的外角和等于180°
D.三角形中至少有一个外角小于和它相邻的内角
5.三角形的一个外角,不大于和它相邻的内角,这个三角形一定是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.非锐角三角形
【课后练习】答案
1.B
2.C
3.B
4.B
5.D
6.B
7.D
8.B
9.A
10.D
11.30°
12.135°
13.75°
14.110°.
15.140°.
