人教版八年级数学上册:11.3.1多边形 课件(共26张PPT)
文档属性
| 名称 | 人教版八年级数学上册:11.3.1多边形 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 360.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 03:54:12 | ||
图片预览







文档简介
(共26张PPT)
第十一章
三角形
11.3.1
多边形
【学习目标】
1.理解多边形的有关概念.
2.理解多边形、多边形的边、角、对角线的概念和意义.
3.掌握正多边形的概念、了解凸多边形的概念
【课前预习】
1.若凸n边形的每个外角都是36°,则从一个顶点出发引的对角线条数是(??
)
A.6
B.7
C.8
D.9
2.一个多边形最少可分割成五个三角形,则它是(
)边形
A.8
B.7
C.6
D.5
3.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点引出的对角线条数是(??
)
A.5条
B.6条
C.9条
D.27条
4.若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是(??
)
A.6
B.8
C.18
D.27
5.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成5个三角形,那么这个多边形有(
)
条对角线
A.13
B.14
C.15
D.5
【课前预习】答案
1.B
2.B
3.B
4.A
5.B
1.什么是三角形?有几条边,几个内角?
2.什么是三角形的外角?有几个外角?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.三角形有三条边,三个内角.
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.一个三角形有三个外角.
复习引入
【学习探究】
多边形
观察图中的图片,其中的房屋结构、蜂巢结构等给我们以
由一些线段
围成的图形的形象,你能从图中想象出几个由一些
线段围成的图形吗?
多边形的概念
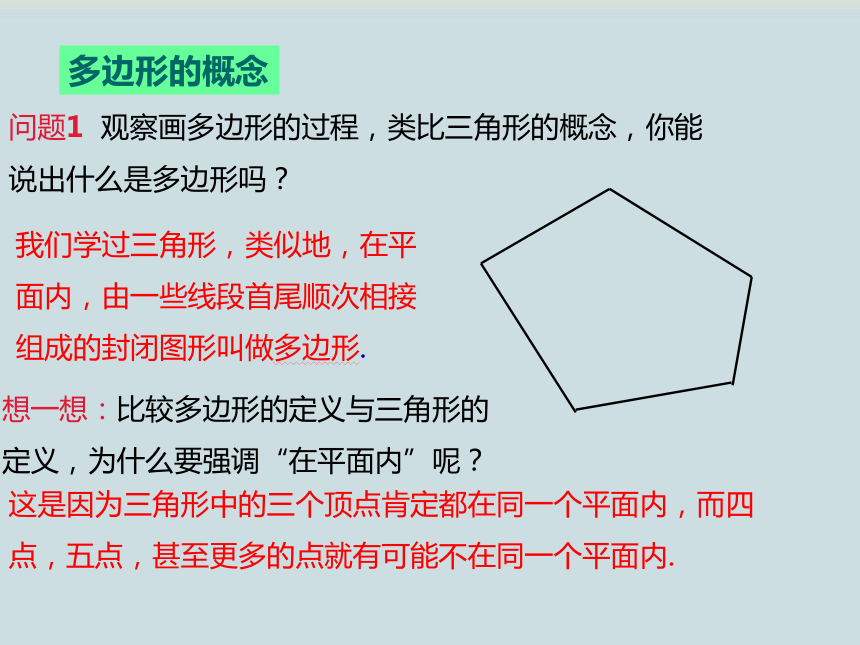
问题1
观察画多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
我们学过三角形,类似地,在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
想一想:比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
多边形按组成它的线段的条数分成三角形、
四
边形、五边形……三角形是最简单的多边形.如果一
个多边形由n条线段组成,那么这个多边形就叫做n
边形.如图,螺母底面的边缘可以设计为六边形,也可
以设计为八边形.
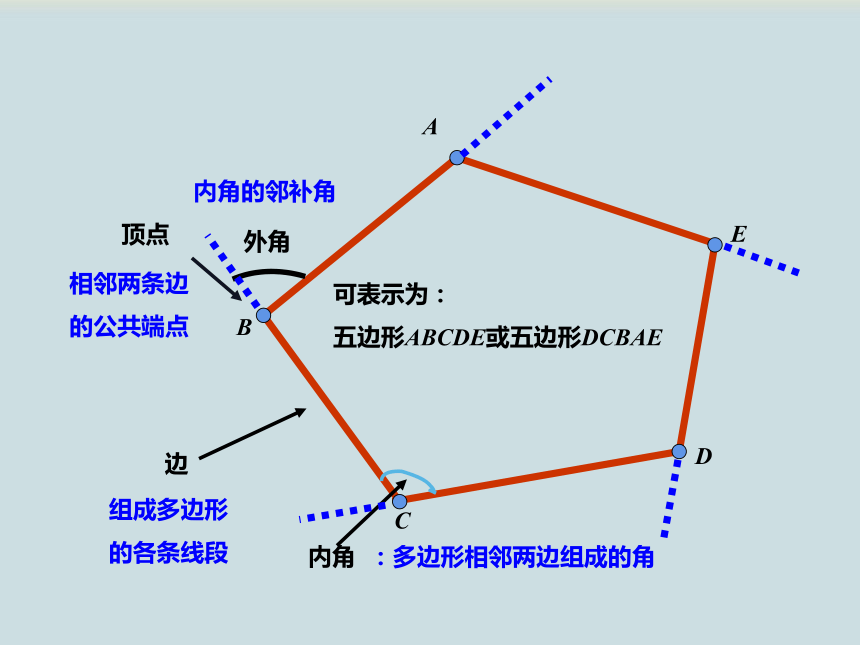
顶点
内角
边
可表示为:
五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
组成多边形的各条线段
相邻两条边的公共端点
问题2
根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
顶点
边
内角:多边形相邻两边组成的角
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
理解多边形的定义需注意:
(1)线段必须“不在同一直线上”且条数要不少于3条;
(2)必须是“平面图形”;
(3)首尾顺次相接.
多边形的对角线
连接多边形不相邻的两个顶点的线段叫做多边形的对角线
A
C
B
D
E
三角形有几条对角线?
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
你能写出每个图形中对角线的总条数吗?如果不能,请画
出所有对角线.
0
2
5
9
知2-讲
你能告诉我二十边形的对角线的总条数吗?五十
边形呢?一百边形呢?n边形呢?
A
B
C
D
E
注意
线段AC是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示.
画一画:画出下列多边形的全部对角线
想一想:
(1)从上面n边形的一个顶点可以作出几条对角线?
(2)n边形的对角线总条数与边数n有怎样的关系?
(1)
(n-3)
(n≥3)
(2)n边形共有对角线
条(n≥3).
边数
3
4
5
6
7
…
n
从一个顶点出发
的对角线的条数
…
总的对角线条数
…
上述对角线分成
的三角形个数
…
0
0
0
1
2
2
2
5
3
3
9
4
4
14
5
n-3
n-2
n(n-3)
2
小结
A
B
C
D
A
B
C
D
我们现在研究的是如图1所示的多边形,整个多边形都在这条直线的同一侧,这样的多边形是凸多边形;
如图2所示的多边形,是凹多边形,但不在现在研究的范围中.今后如果不说明,我们讲的多边形都是凸多边形.
图1
图2
正多边形
定义
像正方形这样,各个角都相等,各条边都相等的多边形.
正三角形
正方形
正五边形
正六边形
想一想:下列多边形是正多边形吗?如不是,请说明为什么?
(四条边都相等)
(四个角都相等)
答:都不是,第一个图形不符合四个角都相等;第二个图形不符合各边都相等.
注意
判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备.
课堂小结
多边形
定义
前提条件是在一个平面内
对角线
它是多边形的一条重要线段,在今后通常作对角线把多边形的问题转化为三角形和四边形的问题
正多
边形
定义既是判定也是性质
【课后练习】
1.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成( )个三角形.
A.6
B.5
C.8
D.7
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6
B.7
C.8
D.9
3.下列属于正多边形的特征的有(
)
(1)各边相等
(2)各个内角相等
(3)各个外角相等
(4)各条对角线都相等
(5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形
A.2个
B.3个
C.4个
D.5个
4.将已知六边形ABCDEF,用对角线将它剖分成互不重叠的4个三角形,那么各种不同的剖分方法种数是( )
A.6
B.8
C.12
D.14
5.下列说法不正确的是(
)
A.各边都相等的多边形是正多边形
B.正多形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
6.从五边形的一个顶点,可以引几条对角线(??
)
A.2
B.3
C.4
D.5
7.一个n边形共有20条对角线,则n的值为(??
)
A.5
B.6
C.8
D.10
8.从十边形的一个顶点出发,作这个十边形的对角线可作(
)
A.6条
B.7条
C.8条
D.9条
9.一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是(??
)
A.6条
B.7条
C.8条
D.9条
10.六边形共有几条对角线( )
A.6
B.7
C.8
D.9
11.过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有k条对角线,则(m-k)n______.
12.过m边形的一个顶点有7条对角线,n边形没有对角线,则n-m=______.
13.选定多边形的一个顶点,连接这个顶点和多边形的其余各顶点,得到了9个三角形,则原多边形的边数是_______.
14.从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成十个三角形,则这个多边形的边数为_____.
15.若凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是___________
【课后练习】答案
1.B
2.C
3.B
4.D
5.A
6.A
7.C
8.B
9.A
10.D
11.125
12.-7
13.11.
14.12
15.6
第十一章
三角形
11.3.1
多边形
【学习目标】
1.理解多边形的有关概念.
2.理解多边形、多边形的边、角、对角线的概念和意义.
3.掌握正多边形的概念、了解凸多边形的概念
【课前预习】
1.若凸n边形的每个外角都是36°,则从一个顶点出发引的对角线条数是(??
)
A.6
B.7
C.8
D.9
2.一个多边形最少可分割成五个三角形,则它是(
)边形
A.8
B.7
C.6
D.5
3.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点引出的对角线条数是(??
)
A.5条
B.6条
C.9条
D.27条
4.若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是(??
)
A.6
B.8
C.18
D.27
5.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成5个三角形,那么这个多边形有(
)
条对角线
A.13
B.14
C.15
D.5
【课前预习】答案
1.B
2.B
3.B
4.A
5.B
1.什么是三角形?有几条边,几个内角?
2.什么是三角形的外角?有几个外角?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.三角形有三条边,三个内角.
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.一个三角形有三个外角.
复习引入
【学习探究】
多边形
观察图中的图片,其中的房屋结构、蜂巢结构等给我们以
由一些线段
围成的图形的形象,你能从图中想象出几个由一些
线段围成的图形吗?
多边形的概念
问题1
观察画多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
我们学过三角形,类似地,在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
想一想:比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
多边形按组成它的线段的条数分成三角形、
四
边形、五边形……三角形是最简单的多边形.如果一
个多边形由n条线段组成,那么这个多边形就叫做n
边形.如图,螺母底面的边缘可以设计为六边形,也可
以设计为八边形.
顶点
内角
边
可表示为:
五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
组成多边形的各条线段
相邻两条边的公共端点
问题2
根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
顶点
边
内角:多边形相邻两边组成的角
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
理解多边形的定义需注意:
(1)线段必须“不在同一直线上”且条数要不少于3条;
(2)必须是“平面图形”;
(3)首尾顺次相接.
多边形的对角线
连接多边形不相邻的两个顶点的线段叫做多边形的对角线
A
C
B
D
E
三角形有几条对角线?
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
你能写出每个图形中对角线的总条数吗?如果不能,请画
出所有对角线.
0
2
5
9
知2-讲
你能告诉我二十边形的对角线的总条数吗?五十
边形呢?一百边形呢?n边形呢?
A
B
C
D
E
注意
线段AC是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示.
画一画:画出下列多边形的全部对角线
想一想:
(1)从上面n边形的一个顶点可以作出几条对角线?
(2)n边形的对角线总条数与边数n有怎样的关系?
(1)
(n-3)
(n≥3)
(2)n边形共有对角线
条(n≥3).
边数
3
4
5
6
7
…
n
从一个顶点出发
的对角线的条数
…
总的对角线条数
…
上述对角线分成
的三角形个数
…
0
0
0
1
2
2
2
5
3
3
9
4
4
14
5
n-3
n-2
n(n-3)
2
小结
A
B
C
D
A
B
C
D
我们现在研究的是如图1所示的多边形,整个多边形都在这条直线的同一侧,这样的多边形是凸多边形;
如图2所示的多边形,是凹多边形,但不在现在研究的范围中.今后如果不说明,我们讲的多边形都是凸多边形.
图1
图2
正多边形
定义
像正方形这样,各个角都相等,各条边都相等的多边形.
正三角形
正方形
正五边形
正六边形
想一想:下列多边形是正多边形吗?如不是,请说明为什么?
(四条边都相等)
(四个角都相等)
答:都不是,第一个图形不符合四个角都相等;第二个图形不符合各边都相等.
注意
判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备.
课堂小结
多边形
定义
前提条件是在一个平面内
对角线
它是多边形的一条重要线段,在今后通常作对角线把多边形的问题转化为三角形和四边形的问题
正多
边形
定义既是判定也是性质
【课后练习】
1.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成( )个三角形.
A.6
B.5
C.8
D.7
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6
B.7
C.8
D.9
3.下列属于正多边形的特征的有(
)
(1)各边相等
(2)各个内角相等
(3)各个外角相等
(4)各条对角线都相等
(5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形
A.2个
B.3个
C.4个
D.5个
4.将已知六边形ABCDEF,用对角线将它剖分成互不重叠的4个三角形,那么各种不同的剖分方法种数是( )
A.6
B.8
C.12
D.14
5.下列说法不正确的是(
)
A.各边都相等的多边形是正多边形
B.正多形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
6.从五边形的一个顶点,可以引几条对角线(??
)
A.2
B.3
C.4
D.5
7.一个n边形共有20条对角线,则n的值为(??
)
A.5
B.6
C.8
D.10
8.从十边形的一个顶点出发,作这个十边形的对角线可作(
)
A.6条
B.7条
C.8条
D.9条
9.一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是(??
)
A.6条
B.7条
C.8条
D.9条
10.六边形共有几条对角线( )
A.6
B.7
C.8
D.9
11.过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有k条对角线,则(m-k)n______.
12.过m边形的一个顶点有7条对角线,n边形没有对角线,则n-m=______.
13.选定多边形的一个顶点,连接这个顶点和多边形的其余各顶点,得到了9个三角形,则原多边形的边数是_______.
14.从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成十个三角形,则这个多边形的边数为_____.
15.若凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是___________
【课后练习】答案
1.B
2.C
3.B
4.D
5.A
6.A
7.C
8.B
9.A
10.D
11.125
12.-7
13.11.
14.12
15.6
