人教版八年级数学上册 12.2全等三角形的判定同步练习题 (word 版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 12.2全等三角形的判定同步练习题 (word 版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 175.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览


文档简介
人教版八年级数学(上)第十二章《全等三角形》12.2全等三角形的判定同步练习题
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.在△ABC和△DEF中,AB=DE,∠A=∠D,若要证明△ABC≌△DEF,还需要补充一个条件,则正确的补充方法是(?
?)。
A.BC=DF
B.AC=EF
C.BC=EF
D.AC=DF
2.如图,在Rt△ABC中,∠ACB=90°,E是AB上一点,且BE=BC,DE⊥AB于E,若AC=8,则AD+DE等于(
)。
A.7
B.8
C.9
D.10
3.在△ABC和△A′B′C′中,下列条件:①∠A=∠A′;②∠B=∠B′;③∠C=∠C′;④AB=A′B′;⑤AC=A′C′;⑥BC=B′C′.其中,能用“SAS”证明△ABC≌△A′B′C′的一组是(
)。
A.①⑤⑥
B.②④⑤
C.①④⑥
D.②④⑥
4.在△ABC和△DEF中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件(
)。
A.AB=ED
B.AB=FD
C.AC=FD
D.∠A=∠F
5.根据下列条件能画出唯一ABC的是(?
?)。
A.AB=3cm,BC=4cm
B.AB=3cm,∠A=30°
C.∠A=30°,∠B=60°,∠C=90°
D.∠A=60°,AB=4cm,AC=3cm
6.如图,点D在AB上,点E在AC上,且∠B=∠C,补充下列一个条件后,仍无法判定△ABE≌△ACD的是(
?
)。
A.AE=AD
B.∠AEB=∠ADC
C.BE=CD
D.AB=AC
7.如图,在四边形ABCD中,AB=CD,AD=BC,O为对角线AC,BD的交点,且AO=CO,BO=DO,则与△AOD全等的是(
)。
A.△ABC
B.△ADC
C.△BCD
D.△COB
8.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于(
)。
???????
A.60°
B.50°
C.45°
D.30°
9.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是(
)。
A.120°
B.125°
C.127°
D.104°
10.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点为卡钳两柄交点,且有,如果圆形工件恰好通过卡钳,则此工件的外径必是之长了,其中的依据是全等三角形的判定条件(?
?)。
A.
B.
C.
D.
二、填空题(本大题共5小题,共15分)
11.在平面直角坐标系中,点A(2,0),B(0,4),当点C的坐标为_________时,△BOC与△ABO全等。
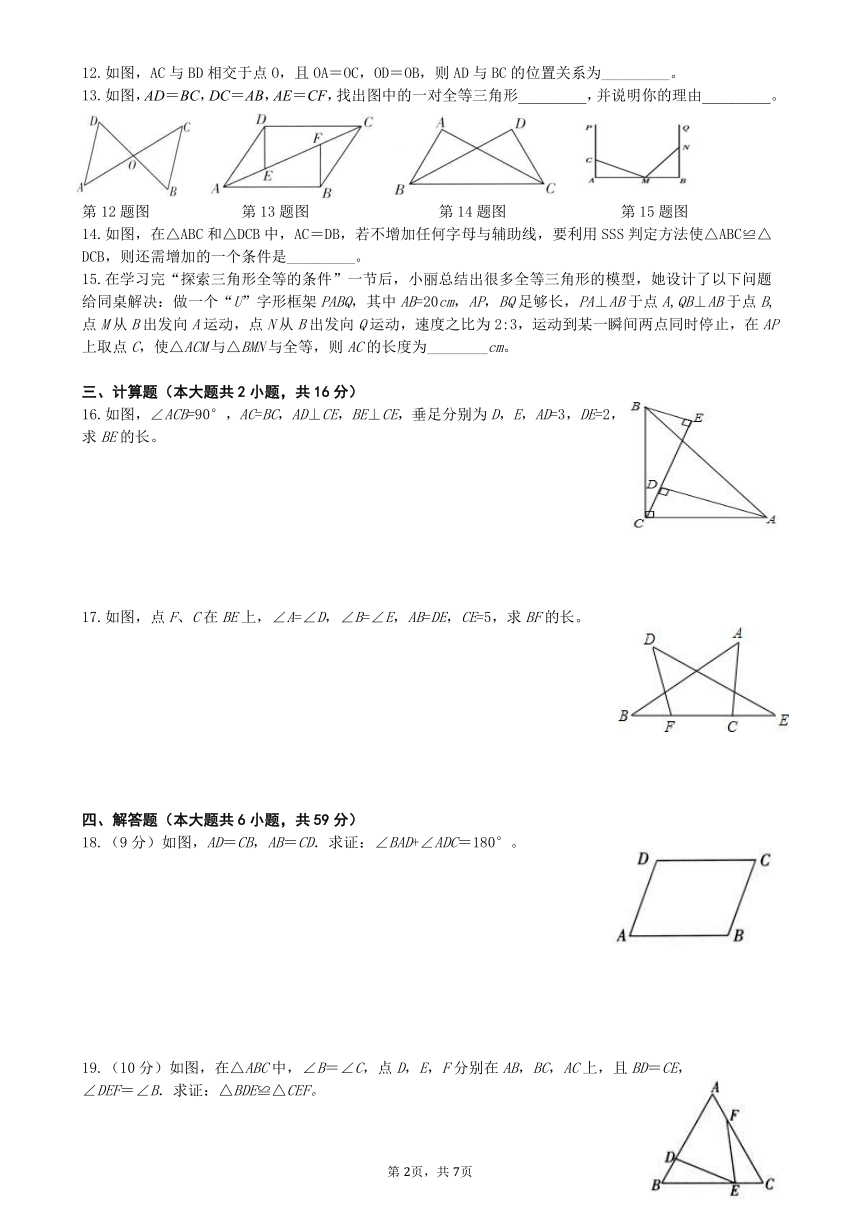
12.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为_________。
13.如图,AD=BC,DC=AB,AE=CF,找出图中的一对全等三角形_________,并说明你的理由_________。
第12题图
第13题图
第14题图
第15题图
14.如图,在△ABC和△DCB中,AC=DB,若不增加任何字母与辅助线,要利用SSS判定方法使△ABC≌△DCB,则还需增加的一个条件是_________。
15.在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“U”字形框架PABQ,其中AB=20cm,AP,BQ足够长,PA⊥AB于点A,QB⊥AB于点B,点M从B出发向A运动,点N从B出发向Q运动,速度之比为2:3,运动到某一瞬间两点同时停止,在AP上取点C,使△ACM与△BMN与全等,则AC的长度为________cm。
三、计算题(本大题共2小题,共16分)
16.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=3,DE=2,求BE的长。
17.如图,点F、C在BE上,∠A=∠D,∠B=∠E,AB=DE,CE=5,求BF的长。
四、解答题(本大题共6小题,共59分)
18.(9分)如图,AD=CB,AB=CD.求证:∠BAD+∠ADC=180°。
19.(10分)如图,在△ABC中,∠B=∠C,点D,E,F分别在AB,BC,AC上,且BD=CE,
∠DEF=∠B.求证:△BDE≌△CEF。
20.(10分)如图,在△ABC中,延长边AC的中线BE到G,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连接AF,AG。
(1)按要求补全图形,并标注字母。
(2)AF与AG的大小关系如何?证明你的结论。
(3)F,A,G三点的位置如何?证明你的结论。
21.(10分)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于点F,BD分别交CE,AE于点G,H。试猜测线段AE和BD的数量和位置关系,并说明理由。
22.(10分)如图(1),AB⊥BD,DE⊥BD,点C是边BD一点,且BC=DE,CD=AB。
(1)试判断AC与CE的位置关系,并说明理由;
(2)如图(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?(注意字母的变化)。
23.(10分)在5×6的方格纸中,每格的边长为1,请按下列要求画图。
(1)在图1中画一个格点△ADE,使△ADE与△ABC全等,且所画格点三角形的顶点均不与点B,C重合。
(2)在图2中画一个面积为7的格点四边形ABCD,且∠BAD为锐角。
参考答案
一、选择题(本大题共10小题,共30分)
1.D
2.B
3.D
4.C
5.D
6.B
7.D
8.A
9.C
10.B
二、填空题(本大题共5小题,共15分)
11.(-2,0)或(-2,4)或(2,4)
12.平行
13.答案不唯一,如△ADC≌△CBA.理由:根据“SSS”,即AD=CB,DC=BA,AC=CA。
14.?AB=DC
15.8或15
三、计算题(本大题共2小题,共16分)
16.解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°
∵AD⊥CE,BE⊥CE,
∴∠D=∠BEC=90°,
∴∠CBE+∠BCD=90°,
∴∠ACD=∠CBE,且AC=BC,∠ADC=∠BEC=90°
∴△ACD≌△CBE(AAS),
∴CE=AD=3,BE=CD,
∵EC=CD+DE,
∴BE=3-2=1。
17.解:在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF.
∴CE=BF,
∵CE=5,
∴BF=5。
四、解答题(本大题共6小题,共59分)
18.证明:连接AC.在△ADC和△CBA中,
,
∴△ADC≌△CBA。
∴∠DCA=∠BAC.
∴AB∥CD。
∴∠BAD+∠ADC=180°。
19.证明:∵∠CED是△BDE的外角,
∴∠CED=∠B+∠BDE,
∵∠CED=∠DEF+∠CEF,∠DEF=∠B,
∴∠BDE=∠CEF;
在△BDE与△CEF中,
,
∴△BDE≌△CEF(ASA)。
20.解:(1)如图所示:
(2)AF=AG。
证明如下:
?在△ADF和△BDC中,
∴△ADF≌△BDC(SAS)。
∴AF=BC。
同理可证△AGE≌△CBE(SAS)。
∴AG=BC。
∴AF=AG。
(3)点F,A,G三点共线。
证明如下:由(2)知△ADF≌△BDC,△AGE≌△CBE,
∴∠FAB=∠ABC,∠GAC=∠ACB。
又∠BAC+∠ABC+∠ACB=180°,
∴∠BAC+∠FAB+∠GAE=180°。
∴F,A,G三点共线。
21.解:猜测AE=BD,AE⊥BD。
理由如下:∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB。
∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB。
∴△ACE≌△DCB(SAS)。
∴AE=BD,∠CAE=∠CDB。
∵∠AFC=∠DFH,
∴∠DHF=∠ACD=90°。
?∴AE⊥BD。
22.解:(1)AC⊥CE。
理由如下:∵AB⊥BD,DE⊥BD,
∴∠B=∠D=90°。
在△ABC和△CDE中,
,
∴△ABC≌△CDE(SAS),
∴∠A=∠DCE,
∵∠A+∠ACB=90°,
∴∠DCE+∠ACB=90°。
∵∠DCE+∠ACB+∠ACE=180°,
∴∠ACE=90°,
∴AC⊥CE。
(2)AC⊥BE。
理由如下:∵由(1)可知△ABC≌△BDE,
∴∠A=∠EBD,
∵∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BFC=90°,
∴AC⊥BE。
23.解:(1)所画格点三角形ADE如下图(画出一种即可):
(2)所画格点四边形ABCD
如下图(画出一种即可):
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.在△ABC和△DEF中,AB=DE,∠A=∠D,若要证明△ABC≌△DEF,还需要补充一个条件,则正确的补充方法是(?
?)。
A.BC=DF
B.AC=EF
C.BC=EF
D.AC=DF
2.如图,在Rt△ABC中,∠ACB=90°,E是AB上一点,且BE=BC,DE⊥AB于E,若AC=8,则AD+DE等于(
)。
A.7
B.8
C.9
D.10
3.在△ABC和△A′B′C′中,下列条件:①∠A=∠A′;②∠B=∠B′;③∠C=∠C′;④AB=A′B′;⑤AC=A′C′;⑥BC=B′C′.其中,能用“SAS”证明△ABC≌△A′B′C′的一组是(
)。
A.①⑤⑥
B.②④⑤
C.①④⑥
D.②④⑥
4.在△ABC和△DEF中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件(
)。
A.AB=ED
B.AB=FD
C.AC=FD
D.∠A=∠F
5.根据下列条件能画出唯一ABC的是(?
?)。
A.AB=3cm,BC=4cm
B.AB=3cm,∠A=30°
C.∠A=30°,∠B=60°,∠C=90°
D.∠A=60°,AB=4cm,AC=3cm
6.如图,点D在AB上,点E在AC上,且∠B=∠C,补充下列一个条件后,仍无法判定△ABE≌△ACD的是(
?
)。
A.AE=AD
B.∠AEB=∠ADC
C.BE=CD
D.AB=AC
7.如图,在四边形ABCD中,AB=CD,AD=BC,O为对角线AC,BD的交点,且AO=CO,BO=DO,则与△AOD全等的是(
)。
A.△ABC
B.△ADC
C.△BCD
D.△COB
8.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于(
)。
???????
A.60°
B.50°
C.45°
D.30°
9.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是(
)。
A.120°
B.125°
C.127°
D.104°
10.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点为卡钳两柄交点,且有,如果圆形工件恰好通过卡钳,则此工件的外径必是之长了,其中的依据是全等三角形的判定条件(?
?)。
A.
B.
C.
D.
二、填空题(本大题共5小题,共15分)
11.在平面直角坐标系中,点A(2,0),B(0,4),当点C的坐标为_________时,△BOC与△ABO全等。
12.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为_________。
13.如图,AD=BC,DC=AB,AE=CF,找出图中的一对全等三角形_________,并说明你的理由_________。
第12题图
第13题图
第14题图
第15题图
14.如图,在△ABC和△DCB中,AC=DB,若不增加任何字母与辅助线,要利用SSS判定方法使△ABC≌△DCB,则还需增加的一个条件是_________。
15.在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“U”字形框架PABQ,其中AB=20cm,AP,BQ足够长,PA⊥AB于点A,QB⊥AB于点B,点M从B出发向A运动,点N从B出发向Q运动,速度之比为2:3,运动到某一瞬间两点同时停止,在AP上取点C,使△ACM与△BMN与全等,则AC的长度为________cm。
三、计算题(本大题共2小题,共16分)
16.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=3,DE=2,求BE的长。
17.如图,点F、C在BE上,∠A=∠D,∠B=∠E,AB=DE,CE=5,求BF的长。
四、解答题(本大题共6小题,共59分)
18.(9分)如图,AD=CB,AB=CD.求证:∠BAD+∠ADC=180°。
19.(10分)如图,在△ABC中,∠B=∠C,点D,E,F分别在AB,BC,AC上,且BD=CE,
∠DEF=∠B.求证:△BDE≌△CEF。
20.(10分)如图,在△ABC中,延长边AC的中线BE到G,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连接AF,AG。
(1)按要求补全图形,并标注字母。
(2)AF与AG的大小关系如何?证明你的结论。
(3)F,A,G三点的位置如何?证明你的结论。
21.(10分)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于点F,BD分别交CE,AE于点G,H。试猜测线段AE和BD的数量和位置关系,并说明理由。
22.(10分)如图(1),AB⊥BD,DE⊥BD,点C是边BD一点,且BC=DE,CD=AB。
(1)试判断AC与CE的位置关系,并说明理由;
(2)如图(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?(注意字母的变化)。
23.(10分)在5×6的方格纸中,每格的边长为1,请按下列要求画图。
(1)在图1中画一个格点△ADE,使△ADE与△ABC全等,且所画格点三角形的顶点均不与点B,C重合。
(2)在图2中画一个面积为7的格点四边形ABCD,且∠BAD为锐角。
参考答案
一、选择题(本大题共10小题,共30分)
1.D
2.B
3.D
4.C
5.D
6.B
7.D
8.A
9.C
10.B
二、填空题(本大题共5小题,共15分)
11.(-2,0)或(-2,4)或(2,4)
12.平行
13.答案不唯一,如△ADC≌△CBA.理由:根据“SSS”,即AD=CB,DC=BA,AC=CA。
14.?AB=DC
15.8或15
三、计算题(本大题共2小题,共16分)
16.解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°
∵AD⊥CE,BE⊥CE,
∴∠D=∠BEC=90°,
∴∠CBE+∠BCD=90°,
∴∠ACD=∠CBE,且AC=BC,∠ADC=∠BEC=90°
∴△ACD≌△CBE(AAS),
∴CE=AD=3,BE=CD,
∵EC=CD+DE,
∴BE=3-2=1。
17.解:在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF.
∴CE=BF,
∵CE=5,
∴BF=5。
四、解答题(本大题共6小题,共59分)
18.证明:连接AC.在△ADC和△CBA中,
,
∴△ADC≌△CBA。
∴∠DCA=∠BAC.
∴AB∥CD。
∴∠BAD+∠ADC=180°。
19.证明:∵∠CED是△BDE的外角,
∴∠CED=∠B+∠BDE,
∵∠CED=∠DEF+∠CEF,∠DEF=∠B,
∴∠BDE=∠CEF;
在△BDE与△CEF中,
,
∴△BDE≌△CEF(ASA)。
20.解:(1)如图所示:
(2)AF=AG。
证明如下:
?在△ADF和△BDC中,
∴△ADF≌△BDC(SAS)。
∴AF=BC。
同理可证△AGE≌△CBE(SAS)。
∴AG=BC。
∴AF=AG。
(3)点F,A,G三点共线。
证明如下:由(2)知△ADF≌△BDC,△AGE≌△CBE,
∴∠FAB=∠ABC,∠GAC=∠ACB。
又∠BAC+∠ABC+∠ACB=180°,
∴∠BAC+∠FAB+∠GAE=180°。
∴F,A,G三点共线。
21.解:猜测AE=BD,AE⊥BD。
理由如下:∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB。
∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB。
∴△ACE≌△DCB(SAS)。
∴AE=BD,∠CAE=∠CDB。
∵∠AFC=∠DFH,
∴∠DHF=∠ACD=90°。
?∴AE⊥BD。
22.解:(1)AC⊥CE。
理由如下:∵AB⊥BD,DE⊥BD,
∴∠B=∠D=90°。
在△ABC和△CDE中,
,
∴△ABC≌△CDE(SAS),
∴∠A=∠DCE,
∵∠A+∠ACB=90°,
∴∠DCE+∠ACB=90°。
∵∠DCE+∠ACB+∠ACE=180°,
∴∠ACE=90°,
∴AC⊥CE。
(2)AC⊥BE。
理由如下:∵由(1)可知△ABC≌△BDE,
∴∠A=∠EBD,
∵∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BFC=90°,
∴AC⊥BE。
23.解:(1)所画格点三角形ADE如下图(画出一种即可):
(2)所画格点四边形ABCD
如下图(画出一种即可):
第2页,共2页
第1页,共1页
