人教版八年级数学上册 11.3多边形及其内角和同步练习题 (word 版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 11.3多边形及其内角和同步练习题 (word 版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 298.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 21:30:22 | ||
图片预览


文档简介
人教版八年级数学(上)第十一章《三角形》11.3多边形及其内角和同步练习题
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为(?
?
)。.
A.90°
B.105°
C.130°
D.120°
2.小明在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2018°,则n等于(
?
)。
A.11
B.12
C.13
D.14
3.把一多边形纸片沿一条直线截下一三角形后变成一个十八边形,则原多边形纸片的边数不可能是(?
)。
A.16
B.17
C.18
D.19
4.下列说法正确的是(?
?
)。
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
5.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )。
A.①②
B.①③
C.②④
D.③④
6.设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是( )。
A.a>b
B.a=b
C.a<b
D.b=a+180°
7.下列图形中不是凸多边形的是(
)。
A.
B.
C.
D.
8.一个四边形没有公共顶点的两个外角之和为p,与这两个外角都不相邻的两个内角的和为q,则(
)。
A.
B.
C.
D.
9.如图,AM是△ABC的中线,△ABC的面积为4
cm2,则△ABM的面积为(
)。
A.8
cm2
B.4
cm2
C.2
cm2
D.以上答案都不对
10.一个三角形的两边长分别为3cm和8cm,则此三角形第三边长可能是( )。
A.3cm
B.5cm
C.7cm
D.11cm
二、填空题(本大题共5小题,共15分)
11.若点M取在n边形的一条边上(不是顶点),再将点M与n边形各顶点连接起来,将此多边形分割成9个三角形,则n边形是_________边形。
12.过m边形的一顶点可以作5条对角线,n边形没有对角线,五边形共有k条对角线,则m=______,n=______,k=______。
13.若过n边形的一个顶点有2m条对角线,m边形没有对角线,k边形有k条对角线,则(n-k)m=_________。
14.如图,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样下去,他第一次回到出发地A点时,一共走的路程是___米。
15.如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为______°。
三、计算题(本大题共2小题,共16分)
16.一个多边形的内角和与外角和的度数总和为12600,求多边形的边数。
17.一个n边形的内角和比它的外角和至少大120°,n的最小值是多少?
四、解答题(本大题共6小题,共59分)
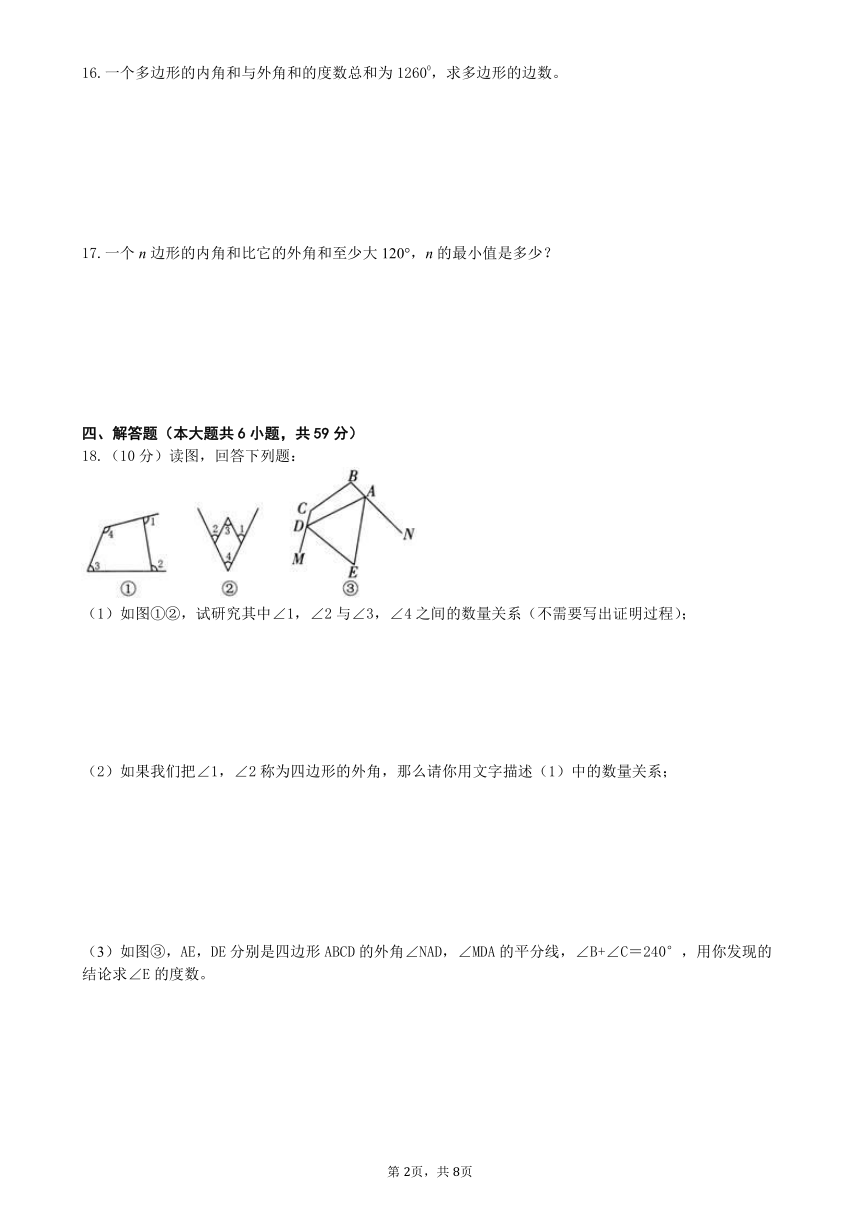
18.(10分)读图,回答下列题:
?
(1)如图①②,试研究其中∠1,∠2与∠3,∠4之间的数量关系(不需要写出证明过程);
(2)如果我们把∠1,∠2称为四边形的外角,那么请你用文字描述(1)中的数量关系;
(3)如图③,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,用你发现的结论求∠E的度数。
19.(10分)阅读下题及解题过程.如图(1)所示,我们知道四边形的内角和为(4-2)×180°=360°,现在将一张四边形的纸剪掉一个角后,剩余纸所有内角的和是多少?
如图(2)所示,剩余纸为五边形,所以剩余纸所有内角的和为(5-2)×180°=540°。
上面的解答过程是否正确?若正确,说出你的判断根据;若不正确,请说明原因,并写出你认为正确的结论。
20.(9分)如图,在五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的邻补角,求∠1+∠2+∠3的度数。
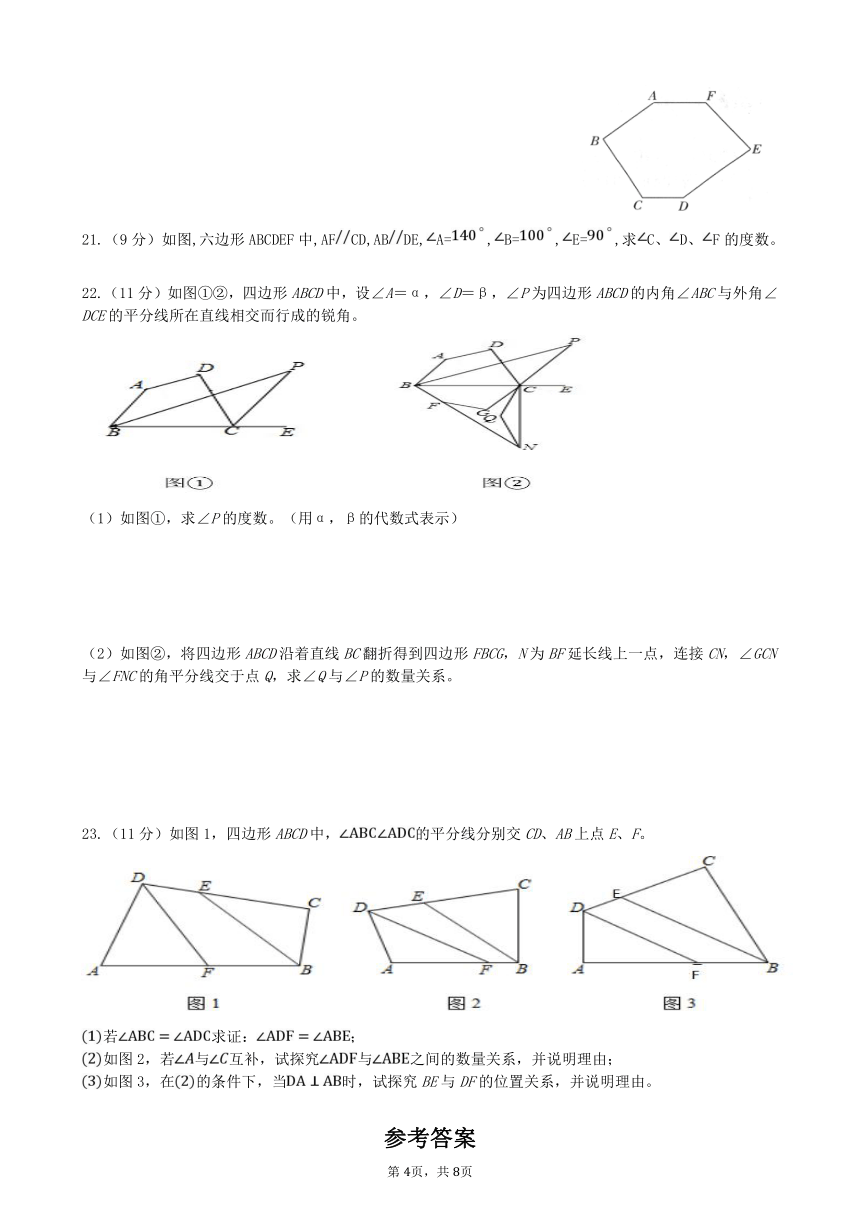
21.(9分)如图,六边形ABCDEF中,AFCD,ABDE,A=,B=,E=,求C、D、F的度数。
22.(11分)如图①②,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交而行成的锐角。
(1)如图①,求∠P的度数。(用α,β的代数式表示)
(2)如图②,将四边形ABCD沿着直线BC翻折得到四边形FBCG,N为BF延长线上一点,连接CN,∠GCN与∠FNC的角平分线交于点Q,求∠Q与∠P的数量关系。
23.(11分)如图1,四边形ABCD中,的平分线分别交CD、AB上点E、F。
若求证:;
如图2,若与互补,试探究与之间的数量关系,并说明理由;
如图3,在的条件下,当时,试探究BE与DF的位置关系,并说明理由。
参考答案
一、选择题(本大题共10小题,共30分)
1.C
2.C
3.A
4.B
5.B
6.B
7.A
8.A
9.C
10.C
二、填空题(本大题共5小题,共15分)
11.十
12.8,3
,5
13.12
14.150
15.95
三、计算题(本大题共2小题,共16分)
16.解:根据多边形的外角和定理知:该多边形的外角和为360°,
多边形的内角和是:1260°-360°=900°,
设多边形的边数是n,
则(n-2)?180°=900°,
解得:n=7.
17.解:(n-2)?180°-360°≥120°,
解得n≥,
所以n的最小值为5。
四、解答题(本大题共6小题,共59分)
18.解:(1)∠1+∠2=∠3+∠4;
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和;
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°,
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴,,
∴,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°。
19.解:不正确.理由如下:
①当剪去一个角成为三角形时,如下图,
剩余纸所有内角的和为360°;
?②当剪去一个角成为四边形时,如下图,
所以剩余纸所有内角的和为(4-2)×180°=360°;
③当剪去一个角成为五边形时,如下图,
?所以剩余纸所有内角的和为(5-2)×180°=540°。
20.解:五边形ABCDE的内角和为:(5-2)×180°=540°,
又∵AB∥CD,
∴∠B+∠C=180°,
∴∠B+∠C+∠CDE+∠DEA+∠EAB=540°,
即180°+(180°-∠3)+(180°-∠2)+(180°-∠1)=540°,
化简得:∠1+∠2+∠3=180°。
∴∠1+∠2+∠3的度数为180°。
21.解:连接AD,
因为AFCD,
所以FAD=ADC。
因为ABDE,
所以BAD=ADE,
所以CDE=BAF=,
所以FAD+ADE=ADC+BAD=BAF=。
因为E=,
所以F=--=。
因为B=,
所以C=--=。
22.解:(1)∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠FBC+(180°-2∠DCP)=180°-2(∠DCP-∠FBC)=180°-2∠P,
∴360°-(α+β)=180°-2∠P,
2∠P=α+β-180°,
∴∠P=(α+β)-90°;
(2)如图,延长CG交BN于H,
∵将四边形ABCD沿着直线BC翻折得到四边形FBCG,
∴∠BFG=∠A=α,∠CGF=∠D=β,
∵∠GHN=∠HFG+∠HGF=180°-α+180°-β,
∴∠GHN=360°-(α+β),且∠P=(α+β)-90°;
∴∠GHN=360°-(2∠P+180°)=180°-2∠P,
∵∠GCN与∠FNC的角平分线交于点Q,
∴∠Q=180°-(∠QCN+∠QNC)
=180°-(∠GCN+∠FNC)
=180°-(180°-∠GHN)
=90°+∠GHN,
∴∠Q=90°+(180°-2∠P)=180°-∠P,
即∠Q+∠P=180°。
23.解:(1)∵DF平分∠ADC,BE平分∠ABC,
∴∠ADF=∠ADC,∠ABE=∠ABC,
又∵∠ABC=∠ADC,
∴∠ADF=∠ABE;
(2)∠ADF与∠ABE互余.理由如下:
∵∠A+∠C=180°,
∴∠ADC+∠ABC=180°,
又∵∠ADF=∠ADC,∠ABE=∠ABC,
∴∠ADF+∠ABE=(∠ADC+∠ABC)=90°;
(3)DF与BE平行.
理由如下:
∵DA⊥AB,
∴在四边形ABCD中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F。
∴∠ABE=∠ABC,∠ADF=∠ADC,
∴∠ABE+∠ADF=90°,
而∠AFD+∠ADF=90°,
∴∠AFD=∠ABE,
∴DF∥BE。
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________得分:___________
一、选择题(本大题共10小题,共30分)
1.若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为(?
?
)。.
A.90°
B.105°
C.130°
D.120°
2.小明在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2018°,则n等于(
?
)。
A.11
B.12
C.13
D.14
3.把一多边形纸片沿一条直线截下一三角形后变成一个十八边形,则原多边形纸片的边数不可能是(?
)。
A.16
B.17
C.18
D.19
4.下列说法正确的是(?
?
)。
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
5.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )。
A.①②
B.①③
C.②④
D.③④
6.设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是( )。
A.a>b
B.a=b
C.a<b
D.b=a+180°
7.下列图形中不是凸多边形的是(
)。
A.
B.
C.
D.
8.一个四边形没有公共顶点的两个外角之和为p,与这两个外角都不相邻的两个内角的和为q,则(
)。
A.
B.
C.
D.
9.如图,AM是△ABC的中线,△ABC的面积为4
cm2,则△ABM的面积为(
)。
A.8
cm2
B.4
cm2
C.2
cm2
D.以上答案都不对
10.一个三角形的两边长分别为3cm和8cm,则此三角形第三边长可能是( )。
A.3cm
B.5cm
C.7cm
D.11cm
二、填空题(本大题共5小题,共15分)
11.若点M取在n边形的一条边上(不是顶点),再将点M与n边形各顶点连接起来,将此多边形分割成9个三角形,则n边形是_________边形。
12.过m边形的一顶点可以作5条对角线,n边形没有对角线,五边形共有k条对角线,则m=______,n=______,k=______。
13.若过n边形的一个顶点有2m条对角线,m边形没有对角线,k边形有k条对角线,则(n-k)m=_________。
14.如图,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样下去,他第一次回到出发地A点时,一共走的路程是___米。
15.如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为______°。
三、计算题(本大题共2小题,共16分)
16.一个多边形的内角和与外角和的度数总和为12600,求多边形的边数。
17.一个n边形的内角和比它的外角和至少大120°,n的最小值是多少?
四、解答题(本大题共6小题,共59分)
18.(10分)读图,回答下列题:
?
(1)如图①②,试研究其中∠1,∠2与∠3,∠4之间的数量关系(不需要写出证明过程);
(2)如果我们把∠1,∠2称为四边形的外角,那么请你用文字描述(1)中的数量关系;
(3)如图③,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,用你发现的结论求∠E的度数。
19.(10分)阅读下题及解题过程.如图(1)所示,我们知道四边形的内角和为(4-2)×180°=360°,现在将一张四边形的纸剪掉一个角后,剩余纸所有内角的和是多少?
如图(2)所示,剩余纸为五边形,所以剩余纸所有内角的和为(5-2)×180°=540°。
上面的解答过程是否正确?若正确,说出你的判断根据;若不正确,请说明原因,并写出你认为正确的结论。
20.(9分)如图,在五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的邻补角,求∠1+∠2+∠3的度数。
21.(9分)如图,六边形ABCDEF中,AFCD,ABDE,A=,B=,E=,求C、D、F的度数。
22.(11分)如图①②,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交而行成的锐角。
(1)如图①,求∠P的度数。(用α,β的代数式表示)
(2)如图②,将四边形ABCD沿着直线BC翻折得到四边形FBCG,N为BF延长线上一点,连接CN,∠GCN与∠FNC的角平分线交于点Q,求∠Q与∠P的数量关系。
23.(11分)如图1,四边形ABCD中,的平分线分别交CD、AB上点E、F。
若求证:;
如图2,若与互补,试探究与之间的数量关系,并说明理由;
如图3,在的条件下,当时,试探究BE与DF的位置关系,并说明理由。
参考答案
一、选择题(本大题共10小题,共30分)
1.C
2.C
3.A
4.B
5.B
6.B
7.A
8.A
9.C
10.C
二、填空题(本大题共5小题,共15分)
11.十
12.8,3
,5
13.12
14.150
15.95
三、计算题(本大题共2小题,共16分)
16.解:根据多边形的外角和定理知:该多边形的外角和为360°,
多边形的内角和是:1260°-360°=900°,
设多边形的边数是n,
则(n-2)?180°=900°,
解得:n=7.
17.解:(n-2)?180°-360°≥120°,
解得n≥,
所以n的最小值为5。
四、解答题(本大题共6小题,共59分)
18.解:(1)∠1+∠2=∠3+∠4;
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和;
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°,
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴,,
∴,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°。
19.解:不正确.理由如下:
①当剪去一个角成为三角形时,如下图,
剩余纸所有内角的和为360°;
?②当剪去一个角成为四边形时,如下图,
所以剩余纸所有内角的和为(4-2)×180°=360°;
③当剪去一个角成为五边形时,如下图,
?所以剩余纸所有内角的和为(5-2)×180°=540°。
20.解:五边形ABCDE的内角和为:(5-2)×180°=540°,
又∵AB∥CD,
∴∠B+∠C=180°,
∴∠B+∠C+∠CDE+∠DEA+∠EAB=540°,
即180°+(180°-∠3)+(180°-∠2)+(180°-∠1)=540°,
化简得:∠1+∠2+∠3=180°。
∴∠1+∠2+∠3的度数为180°。
21.解:连接AD,
因为AFCD,
所以FAD=ADC。
因为ABDE,
所以BAD=ADE,
所以CDE=BAF=,
所以FAD+ADE=ADC+BAD=BAF=。
因为E=,
所以F=--=。
因为B=,
所以C=--=。
22.解:(1)∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠FBC+(180°-2∠DCP)=180°-2(∠DCP-∠FBC)=180°-2∠P,
∴360°-(α+β)=180°-2∠P,
2∠P=α+β-180°,
∴∠P=(α+β)-90°;
(2)如图,延长CG交BN于H,
∵将四边形ABCD沿着直线BC翻折得到四边形FBCG,
∴∠BFG=∠A=α,∠CGF=∠D=β,
∵∠GHN=∠HFG+∠HGF=180°-α+180°-β,
∴∠GHN=360°-(α+β),且∠P=(α+β)-90°;
∴∠GHN=360°-(2∠P+180°)=180°-2∠P,
∵∠GCN与∠FNC的角平分线交于点Q,
∴∠Q=180°-(∠QCN+∠QNC)
=180°-(∠GCN+∠FNC)
=180°-(180°-∠GHN)
=90°+∠GHN,
∴∠Q=90°+(180°-2∠P)=180°-∠P,
即∠Q+∠P=180°。
23.解:(1)∵DF平分∠ADC,BE平分∠ABC,
∴∠ADF=∠ADC,∠ABE=∠ABC,
又∵∠ABC=∠ADC,
∴∠ADF=∠ABE;
(2)∠ADF与∠ABE互余.理由如下:
∵∠A+∠C=180°,
∴∠ADC+∠ABC=180°,
又∵∠ADF=∠ADC,∠ABE=∠ABC,
∴∠ADF+∠ABE=(∠ADC+∠ABC)=90°;
(3)DF与BE平行.
理由如下:
∵DA⊥AB,
∴在四边形ABCD中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F。
∴∠ABE=∠ABC,∠ADF=∠ADC,
∴∠ABE+∠ADF=90°,
而∠AFD+∠ADF=90°,
∴∠AFD=∠ABE,
∴DF∥BE。
第2页,共2页
第1页,共1页
