北师版八年级数学上册 1.3勾股定理的应用同步训练卷 (word 版 含答案)
文档属性
| 名称 | 北师版八年级数学上册 1.3勾股定理的应用同步训练卷 (word 版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 341.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 21:33:32 | ||
图片预览


文档简介
北师版八年级数学上册
1.3勾股定理的应用
同步训练卷
一、选择题(共10小题,3
10=30)
1.如图是一块长、宽、高分别是6
cm,4
cm和3
cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是(
)
A.85
B.97
C.109
D.81
2.一个圆柱形的油桶高120
cm,底面直径为50
cm,则桶内所能容下的最长的木棒长为(
)
A.5
cm
B.100
cm
C.120
cm
D.130
cm
3.如图,有两棵树,一棵树高8
m,另一棵树高3
m,两棵树相距12
m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.12
m
B.14
m
C.13
m
D.15
m
4.如图,在水塔O的东北方向32
m处有一抽水站A,在水塔的东南方向24
m处有一建筑工地B,在A,B间建一条直水管,则水管的长为( )
A.45
m
B.40
m
C.50
m
D.56
m
5.如图,甲货船以16
n
mile/h的速度从港口A出发向东北方向航行,乙货船以12
n
mile/h的速度同时从港口A出发向东南方向航行,离开港口3
h时两船相距( )
A.35
n
mile B.50
n
mile C.60
n
mile D.40
n
mile
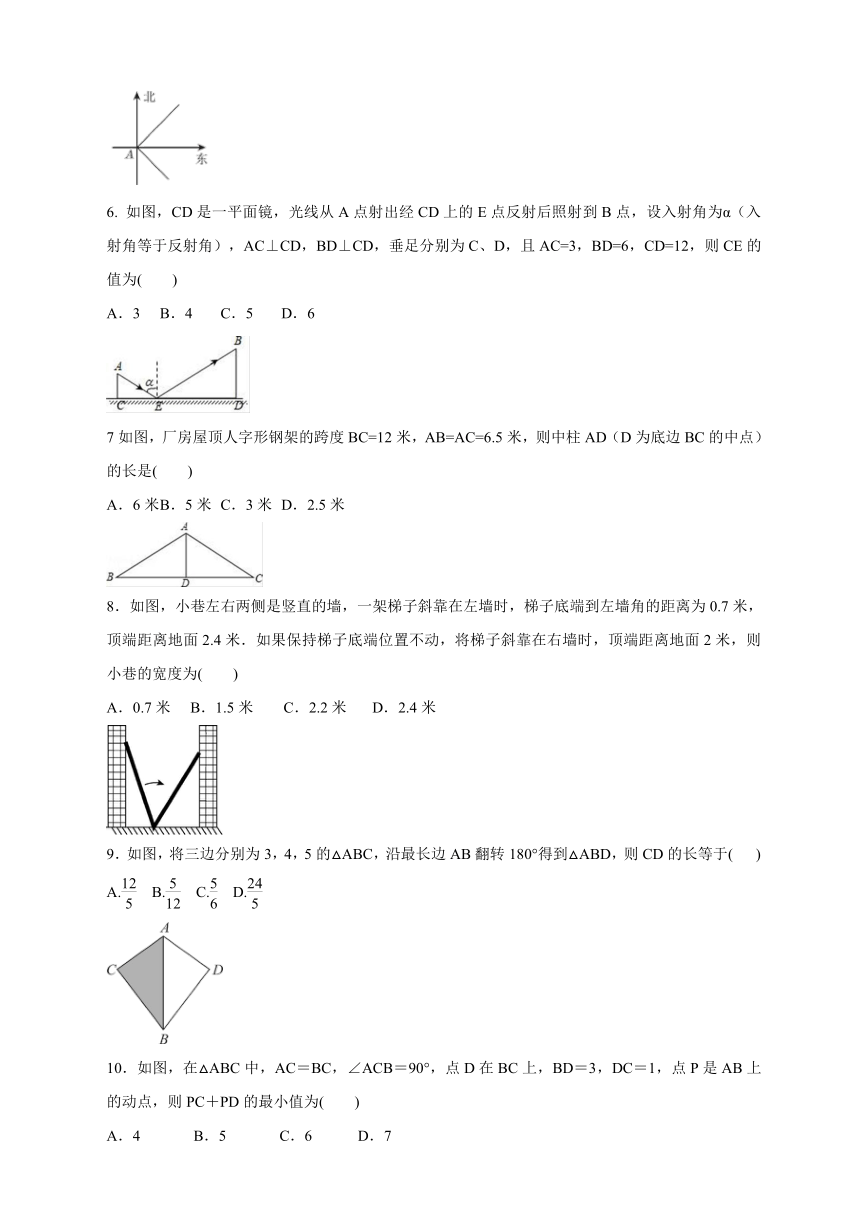
6.
如图,CD是一平面镜,光线从A点射出经CD上的E点反射后照射到B点,设入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=12,则CE的值为( )
A.3
B.4
C.5
D.6
7如图,厂房屋顶人字形钢架的跨度BC=12米,AB=AC=6.5米,则中柱AD(D为底边BC的中点)的长是( )
A.6米
B.5米
C.3米
D.2.5米
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
9.如图,将三边分别为3,4,5的△ABC,沿最长边AB翻转180°得到△ABD,则CD的长等于(
)
A.
B.
C.
D.
10.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4
B.5
C.6
D.7
二.填空题(共8小题,3
8=24)
11.若要登上12
m高的建筑物,为了安全,需使梯子底端离建筑物底部5
m,则至少需要________m长的梯子.
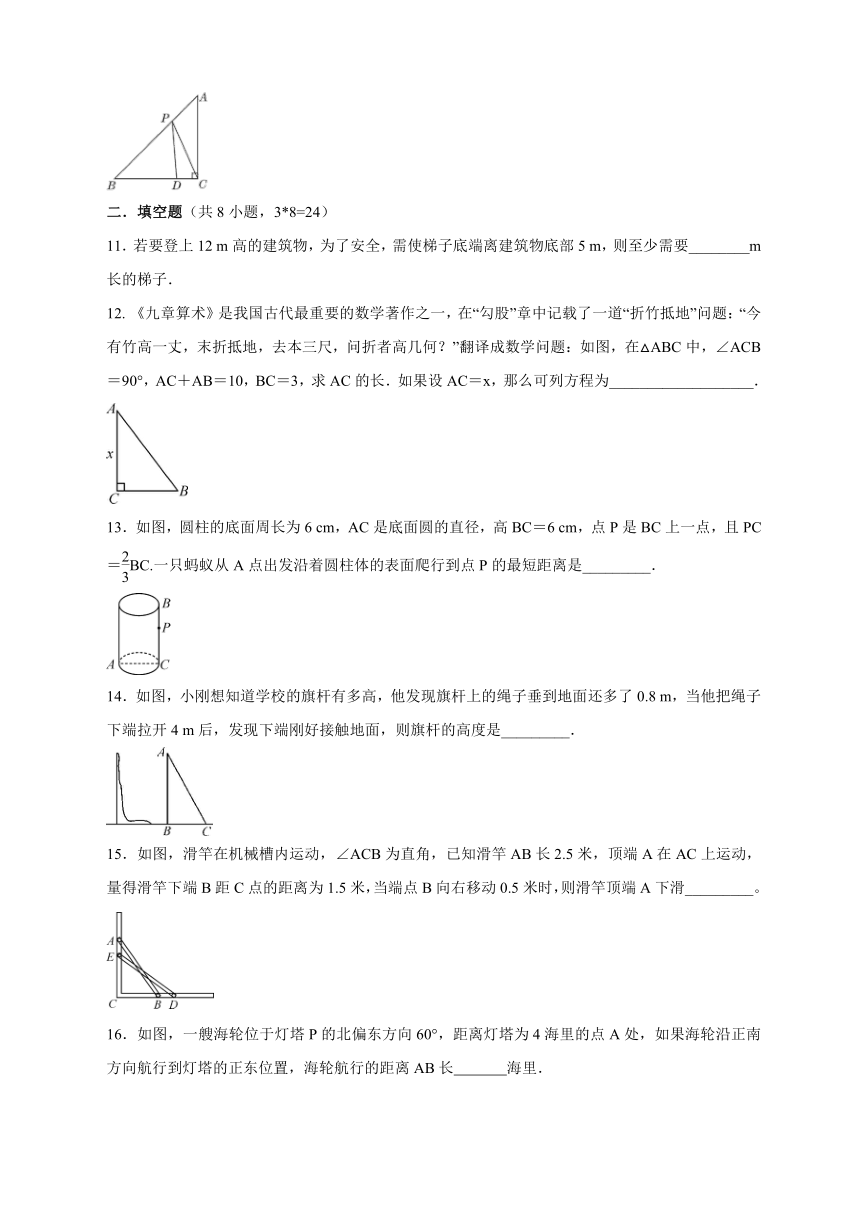
12.
《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题:如图,在△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.如果设AC=x,那么可列方程为___________________.
13.如图,圆柱的底面周长为6
cm,AC是底面圆的直径,高BC=6
cm,点P是BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是_________.
14.如图,小刚想知道学校的旗杆有多高,他发现旗杆上的绳子垂到地面还多了0.8
m,当他把绳子下端拉开4
m后,发现下端刚好接触地面,则旗杆的高度是_________.
15.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶端A在AC上运动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,则滑竿顶端A下滑_________。
16.如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长
海里.
17.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm到D,则橡皮筋被拉长了
cm.
18.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为
cm(杯壁厚度不计).
三.解答题(共7小题,
46分)
19.(6分)
如图是一个三级台阶,它的每一级的长、宽、高分别为20
dm,3
dm,2
dm,点A和点B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶面爬行到B点的最短路程是多少?
20.(6分)
如图,一个无盖的长方体形盒子的长、宽、高分别为8
cm,8
cm,12
cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短路程是多少?
21.(6分)
如图,小李准备建一个蔬菜大棚,棚宽4米,高3米,长20米,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请你帮他计算阳光透过的最大面积.
22.(6分)
如图,小明从电线杆AB顶牵下长25
m的绳子BC,他用手牵住绳子离地1
m.已知小明距电线杆有24
m(AD),求电线杆的高度AB.
23.(6分)
有一个高为1.5
m,半径是1
m的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒.已知铁棒在油桶外的部分为0.5
m,问:这根铁棒有多长?
24.(8分)
如图,已知长方体的长AC=2
cm,宽BC=1
cm,高AA′=4
cm,如果一只蚂蚁沿长方体的表面从A点爬到B′点,那么最短路程是多少?
25.(8分)
有一只蚂蚁要从一个圆柱形玻璃杯的点A处沿侧面爬到点B处(点A,B均在玻璃杯外部),如图,已知杯子高8
cm,点B距杯口3
cm,杯子底面半径为4
cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
参考答案
1-5
ADCBC
6-10BDCDB
11.
13
12.
(10-x)2=x2+32
13.
5cm
14.
9.6m
15.
0.5米
16.
2
17.
2
18.
20
19.
解:如图,应把台阶看成是纸片折成的,拉平(没高度)成一张长方形,
长为3×3+2×3=15(dm),宽为20
dm)的纸.
所以AB2=152+202=625(dm2).
所以AB=25
dm,
即蚂蚁沿着台阶面爬行到B点的最短路程是25
dm
20.
解:由盒子的展开图可知,AB为最短的线路(如答图).
由勾股定理,得AB2=(8+8)2+122=400,
所以AB=20(cm).即蚂蚁要爬行的最短路程是20
cm.
21.
解:在直角三角形中,由勾股定理,得直角三角形的斜边长为5米,
所以长方形塑料薄膜的面积是5×20=100(米2).
答:阳光透过的最大面积是100平方米.
22.
解:过点C作CE⊥AB于点E,
则AE=CD=1
m,CE=AD=24
m.
由勾股定理,得BE2=BC2-CE2=252-242=49,
所以BE=7
m.所以AB=7+1=8
(m).
23.
解:设将铁棒伸入油桶中的长度为x
m.
最长时,x2=1.52+22,解得x=2.5.
所以最长是2.5+0.5=3(m).
最短时,x=1.5.所以最短是1.5+0.5=2(m).
答:这根铁棒的长应在2
m~3
m之间.
24.
解:根据题意,有以下三种情况:
(1)如图①,连接AB′,AB′2=AB2+BB′2=(2+1)2+42=25;
(2)如图②,连接AB′,AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)如图③,连接AB′,AB′2=AD2+B′D2=12+(4+2)2=1+36=37.
综上所述,最短路程应为如图①
所示的情况,此时AB′2=25,即AB′=5
cm.故最短路程是5
cm.
25.
解:将圆柱的侧面从点A处竖直向上剪开,此圆柱的侧面展开图为长方形ACDE,如图,其中AC的长为圆柱的底面周长,连接AB,过点B作AE的垂线交AE于点E′,交CD于点D′.
所以AC=2πr≈2×3×4=24(cm).
则E′B=E′D′=AC≈×24=12(cm).
又因为EA=8
cm,EE′=3
cm,
所以AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2≈52+122=132,
所以AB≈13
cm.
因为两点之间,线段最短,
所以蚂蚁从A点爬到B点的最短距离约为13
cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
1.3勾股定理的应用
同步训练卷
一、选择题(共10小题,3
10=30)
1.如图是一块长、宽、高分别是6
cm,4
cm和3
cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是(
)
A.85
B.97
C.109
D.81
2.一个圆柱形的油桶高120
cm,底面直径为50
cm,则桶内所能容下的最长的木棒长为(
)
A.5
cm
B.100
cm
C.120
cm
D.130
cm
3.如图,有两棵树,一棵树高8
m,另一棵树高3
m,两棵树相距12
m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.12
m
B.14
m
C.13
m
D.15
m
4.如图,在水塔O的东北方向32
m处有一抽水站A,在水塔的东南方向24
m处有一建筑工地B,在A,B间建一条直水管,则水管的长为( )
A.45
m
B.40
m
C.50
m
D.56
m
5.如图,甲货船以16
n
mile/h的速度从港口A出发向东北方向航行,乙货船以12
n
mile/h的速度同时从港口A出发向东南方向航行,离开港口3
h时两船相距( )
A.35
n
mile B.50
n
mile C.60
n
mile D.40
n
mile
6.
如图,CD是一平面镜,光线从A点射出经CD上的E点反射后照射到B点,设入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=12,则CE的值为( )
A.3
B.4
C.5
D.6
7如图,厂房屋顶人字形钢架的跨度BC=12米,AB=AC=6.5米,则中柱AD(D为底边BC的中点)的长是( )
A.6米
B.5米
C.3米
D.2.5米
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
9.如图,将三边分别为3,4,5的△ABC,沿最长边AB翻转180°得到△ABD,则CD的长等于(
)
A.
B.
C.
D.
10.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4
B.5
C.6
D.7
二.填空题(共8小题,3
8=24)
11.若要登上12
m高的建筑物,为了安全,需使梯子底端离建筑物底部5
m,则至少需要________m长的梯子.
12.
《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题:如图,在△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.如果设AC=x,那么可列方程为___________________.
13.如图,圆柱的底面周长为6
cm,AC是底面圆的直径,高BC=6
cm,点P是BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是_________.
14.如图,小刚想知道学校的旗杆有多高,他发现旗杆上的绳子垂到地面还多了0.8
m,当他把绳子下端拉开4
m后,发现下端刚好接触地面,则旗杆的高度是_________.
15.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶端A在AC上运动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,则滑竿顶端A下滑_________。
16.如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长
海里.
17.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm到D,则橡皮筋被拉长了
cm.
18.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为
cm(杯壁厚度不计).
三.解答题(共7小题,
46分)
19.(6分)
如图是一个三级台阶,它的每一级的长、宽、高分别为20
dm,3
dm,2
dm,点A和点B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶面爬行到B点的最短路程是多少?
20.(6分)
如图,一个无盖的长方体形盒子的长、宽、高分别为8
cm,8
cm,12
cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短路程是多少?
21.(6分)
如图,小李准备建一个蔬菜大棚,棚宽4米,高3米,长20米,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请你帮他计算阳光透过的最大面积.
22.(6分)
如图,小明从电线杆AB顶牵下长25
m的绳子BC,他用手牵住绳子离地1
m.已知小明距电线杆有24
m(AD),求电线杆的高度AB.
23.(6分)
有一个高为1.5
m,半径是1
m的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒.已知铁棒在油桶外的部分为0.5
m,问:这根铁棒有多长?
24.(8分)
如图,已知长方体的长AC=2
cm,宽BC=1
cm,高AA′=4
cm,如果一只蚂蚁沿长方体的表面从A点爬到B′点,那么最短路程是多少?
25.(8分)
有一只蚂蚁要从一个圆柱形玻璃杯的点A处沿侧面爬到点B处(点A,B均在玻璃杯外部),如图,已知杯子高8
cm,点B距杯口3
cm,杯子底面半径为4
cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
参考答案
1-5
ADCBC
6-10BDCDB
11.
13
12.
(10-x)2=x2+32
13.
5cm
14.
9.6m
15.
0.5米
16.
2
17.
2
18.
20
19.
解:如图,应把台阶看成是纸片折成的,拉平(没高度)成一张长方形,
长为3×3+2×3=15(dm),宽为20
dm)的纸.
所以AB2=152+202=625(dm2).
所以AB=25
dm,
即蚂蚁沿着台阶面爬行到B点的最短路程是25
dm
20.
解:由盒子的展开图可知,AB为最短的线路(如答图).
由勾股定理,得AB2=(8+8)2+122=400,
所以AB=20(cm).即蚂蚁要爬行的最短路程是20
cm.
21.
解:在直角三角形中,由勾股定理,得直角三角形的斜边长为5米,
所以长方形塑料薄膜的面积是5×20=100(米2).
答:阳光透过的最大面积是100平方米.
22.
解:过点C作CE⊥AB于点E,
则AE=CD=1
m,CE=AD=24
m.
由勾股定理,得BE2=BC2-CE2=252-242=49,
所以BE=7
m.所以AB=7+1=8
(m).
23.
解:设将铁棒伸入油桶中的长度为x
m.
最长时,x2=1.52+22,解得x=2.5.
所以最长是2.5+0.5=3(m).
最短时,x=1.5.所以最短是1.5+0.5=2(m).
答:这根铁棒的长应在2
m~3
m之间.
24.
解:根据题意,有以下三种情况:
(1)如图①,连接AB′,AB′2=AB2+BB′2=(2+1)2+42=25;
(2)如图②,连接AB′,AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)如图③,连接AB′,AB′2=AD2+B′D2=12+(4+2)2=1+36=37.
综上所述,最短路程应为如图①
所示的情况,此时AB′2=25,即AB′=5
cm.故最短路程是5
cm.
25.
解:将圆柱的侧面从点A处竖直向上剪开,此圆柱的侧面展开图为长方形ACDE,如图,其中AC的长为圆柱的底面周长,连接AB,过点B作AE的垂线交AE于点E′,交CD于点D′.
所以AC=2πr≈2×3×4=24(cm).
则E′B=E′D′=AC≈×24=12(cm).
又因为EA=8
cm,EE′=3
cm,
所以AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2≈52+122=132,
所以AB≈13
cm.
因为两点之间,线段最短,
所以蚂蚁从A点爬到B点的最短距离约为13
cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
