人教版 六年级上册数学教案 - 第四单元 第1课时 比的意义(表格版)
文档属性
| 名称 | 人教版 六年级上册数学教案 - 第四单元 第1课时 比的意义(表格版) |
|
|
| 格式 | doc | ||
| 文件大小 | 41.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 00:00:00 | ||
图片预览

文档简介
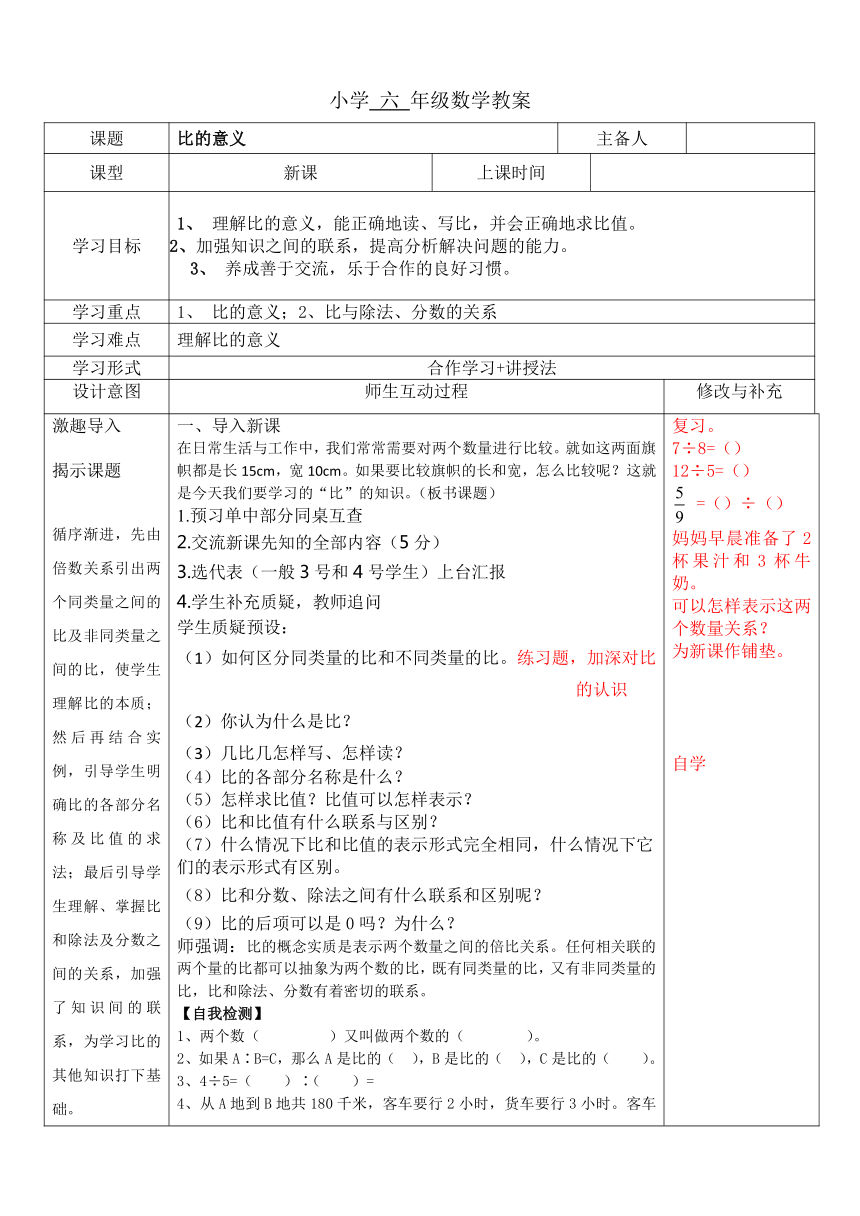
小学 六 年级数学教案
课题 比的意义 主备人
课型 新课 上课时间
学习目标 1、 理解比的意义,能正确地读、写比,并会正确地求比值。
2、加强知识之间的联系,提高分析解决问题的能力。
情 3、 养成善于交流,乐于合作的良好习惯。
学习重点 1、 比的意义;2、比与除法、分数的关系
学习难点 理解比的意义
学习形式 合作学习+讲授法
设计意图 师生互动过程 修改与补充
激趣导入
揭示课题
循序渐进,先由倍数关系引出两个同类量之间的比及非同类量之间的比,使学生理解比的本质;然后再结合实例,引导学生明确比的各部分名称及比值的求法;最后引导学生理解、掌握比和除法及分数之间的关系,加强了知识间的联系,为学习比的其他知识打下基础。
一、导入新课
在日常生活与工作中,我们常常需要对两个数量进行比较。就如这两面旗帜都是长15cm,宽10cm。如果要比较旗帜的长和宽,怎么比较呢?这就是今天我们要学习的“比”的知识。(板书课题)
1.预习单中部分同桌互查
2.交流新课先知的全部内容(5分)
3.选代表(一般3号和4号学生)上台汇报
4.学生补充质疑,教师追问
学生质疑预设:
(1)如何区分同类量的比和不同类量的比。练习题,加深对比的认识
(2)你认为什么是比?
(3)几比几怎样写、怎样读?
(4)比的各部分名称是什么?
(5)怎样求比值?比值可以怎样表示?
(6)比和比值有什么联系与区别?
(7)什么情况下比和比值的表示形式完全相同,什么情况下它们的表示形式有区别。
(8)比和分数、除法之间有什么联系和区别呢?
(9)比的后项可以是0吗?为什么?
师强调:比的概念实质是表示两个数量之间的倍比关系。任何相关联的两个量的比都可以抽象为两个数的比,既有同类量的比,又有非同类量的比,比和除法、分数有着密切的联系。
【自我检测】
1、两个数( )又叫做两个数的( )。
2、如果A∶B=C,那么A是比的( ),B是比的( ),C是比的( )。
3、4÷5=( )∶( )=
4、从A地到B地共180千米,客车要行2小时,货车要行3小时。客车所行的路程与所用时间的比是( ),比值是( );这个比值表示( )。客车所用的时间与货车所用的时间比是( ),比值是( );货车与客车的速度比是( ),比值是( );客车与货车所行的路程比是( ),比值是( )。
5、甲数是乙数的,乙数与甲数的比是( )。
6、在97克水里放入3克盐,盐与水的比是( ),比值是( );水与盐水的比是( ),比值是( )。
7、甲数除以乙数的商是1 .4,乙数与甲数的比是( )。
【巩固练习】
求比值。
0.75∶1.5 ∶ 4∶
小时∶45分 0.3平方米∶9平方分米
【课堂检测】
根据题目中提供的信息,寻找合适的量组成比。
李芳今年12岁,是一名小学五年级的学生,班里共有42名学生。王刚的爸爸今年36 岁,在保险公司上班,年薪50000元,王刚的妈妈每月工资3000元,她所在单位有90人。
复习。
7÷8=()
12÷5=()
=()÷()
妈妈早晨准备了2杯果汁和3杯牛奶。
可以怎样表示这两个数量关系?
为新课作铺垫。
自学
补充乒乓球比赛中2:0是比吗?
学生讨论
总结;各类比赛中的比不是我们这节课学习的比,它只是一种分形式,是小的,是相差关系,不是相除关系。
板书设计 比的意义
两数相除又叫两个数的比。
前项:后项=前项÷后项
安全提示语;同学摔倒楼梯上,自己伸手快帮忙。
教学反思:
充分发挥学生的主动性,让学生真正成为学习的小主人。在学习比的各部分名称及读法。写法时,采用了让学生自学课本的方式。因为自学课本也是学生探索问题,解决问题的重要途径。
不足之处;
1、要注重板书。2、及时总结。3、要适当对学生爱国教育,从主题图出发。4、衔接过度语一定要组织语言精炼。
课题 比的意义 主备人
课型 新课 上课时间
学习目标 1、 理解比的意义,能正确地读、写比,并会正确地求比值。
2、加强知识之间的联系,提高分析解决问题的能力。
情 3、 养成善于交流,乐于合作的良好习惯。
学习重点 1、 比的意义;2、比与除法、分数的关系
学习难点 理解比的意义
学习形式 合作学习+讲授法
设计意图 师生互动过程 修改与补充
激趣导入
揭示课题
循序渐进,先由倍数关系引出两个同类量之间的比及非同类量之间的比,使学生理解比的本质;然后再结合实例,引导学生明确比的各部分名称及比值的求法;最后引导学生理解、掌握比和除法及分数之间的关系,加强了知识间的联系,为学习比的其他知识打下基础。
一、导入新课
在日常生活与工作中,我们常常需要对两个数量进行比较。就如这两面旗帜都是长15cm,宽10cm。如果要比较旗帜的长和宽,怎么比较呢?这就是今天我们要学习的“比”的知识。(板书课题)
1.预习单中部分同桌互查
2.交流新课先知的全部内容(5分)
3.选代表(一般3号和4号学生)上台汇报
4.学生补充质疑,教师追问
学生质疑预设:
(1)如何区分同类量的比和不同类量的比。练习题,加深对比的认识
(2)你认为什么是比?
(3)几比几怎样写、怎样读?
(4)比的各部分名称是什么?
(5)怎样求比值?比值可以怎样表示?
(6)比和比值有什么联系与区别?
(7)什么情况下比和比值的表示形式完全相同,什么情况下它们的表示形式有区别。
(8)比和分数、除法之间有什么联系和区别呢?
(9)比的后项可以是0吗?为什么?
师强调:比的概念实质是表示两个数量之间的倍比关系。任何相关联的两个量的比都可以抽象为两个数的比,既有同类量的比,又有非同类量的比,比和除法、分数有着密切的联系。
【自我检测】
1、两个数( )又叫做两个数的( )。
2、如果A∶B=C,那么A是比的( ),B是比的( ),C是比的( )。
3、4÷5=( )∶( )=
4、从A地到B地共180千米,客车要行2小时,货车要行3小时。客车所行的路程与所用时间的比是( ),比值是( );这个比值表示( )。客车所用的时间与货车所用的时间比是( ),比值是( );货车与客车的速度比是( ),比值是( );客车与货车所行的路程比是( ),比值是( )。
5、甲数是乙数的,乙数与甲数的比是( )。
6、在97克水里放入3克盐,盐与水的比是( ),比值是( );水与盐水的比是( ),比值是( )。
7、甲数除以乙数的商是1 .4,乙数与甲数的比是( )。
【巩固练习】
求比值。
0.75∶1.5 ∶ 4∶
小时∶45分 0.3平方米∶9平方分米
【课堂检测】
根据题目中提供的信息,寻找合适的量组成比。
李芳今年12岁,是一名小学五年级的学生,班里共有42名学生。王刚的爸爸今年36 岁,在保险公司上班,年薪50000元,王刚的妈妈每月工资3000元,她所在单位有90人。
复习。
7÷8=()
12÷5=()
=()÷()
妈妈早晨准备了2杯果汁和3杯牛奶。
可以怎样表示这两个数量关系?
为新课作铺垫。
自学
补充乒乓球比赛中2:0是比吗?
学生讨论
总结;各类比赛中的比不是我们这节课学习的比,它只是一种分形式,是小的,是相差关系,不是相除关系。
板书设计 比的意义
两数相除又叫两个数的比。
前项:后项=前项÷后项
安全提示语;同学摔倒楼梯上,自己伸手快帮忙。
教学反思:
充分发挥学生的主动性,让学生真正成为学习的小主人。在学习比的各部分名称及读法。写法时,采用了让学生自学课本的方式。因为自学课本也是学生探索问题,解决问题的重要途径。
不足之处;
1、要注重板书。2、及时总结。3、要适当对学生爱国教育,从主题图出发。4、衔接过度语一定要组织语言精炼。
