湖南省长沙市2019-2020学年八年级期末数学能力模拟测试试卷3(word版,含答案)
文档属性
| 名称 | 湖南省长沙市2019-2020学年八年级期末数学能力模拟测试试卷3(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 584.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 14:43:31 | ||
图片预览




文档简介
长沙市2020年八年级期末学业水平考试
数
学
(模拟试卷2)
时量:120分钟
总分:150分
选择题(本题共10个小题,每小题4分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填在相应的表格内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.英国作家奥斯森有言“The
best
gift
that
a
tree
is
a
godsend”,总所周知,树林给我们创造了无限的价值。在长白山,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,请问小鸟至少飞行
A.4米
B.8米
C.10米
D.12米
2.在□ABCD中,下列结论一定正确的是
A.AC⊥BD
B.∠A+∠B=180°
C.AB=AD
D.∠A≠∠C
3.若x<2,化简
的正确结果是
A.-1
B.1
C.2x-5
D.5-2x
4.李老师对本班40名学生的一次数学测试成绩作了统计,列出如下的统计表,则本班这次数学测试中A等的人数是
A.16
B.14
C.4
D.6
5.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的
A.测量对角线是否相互平分
B.
测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.
测量对角线是否相等
6.下列函数中,y随x的增大而减少的函数是
A.y=2x+4
B.y=?2+4x
C.y=?2x+8
D.y=2x
7.点A(m,1)在函数y=3x的图象上,则m的值是
A.
B.1
C.2
D.3
8.如图,在□ABCD中,∠BAD=60°,且它的平分线与BC的延长线交于点E,与DC交于点F,又点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为
A.
8
B.
C.
4
D.
二、填空题(本题5个小题,每小题4分,共20分)
9.把分母有理化后得到的最简答案为
;
10.已知一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(0,?2)和点B(1,0),则y=
;
11.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘.经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中有标记的鱼有3条,则鱼
塘中估计有
条鱼;
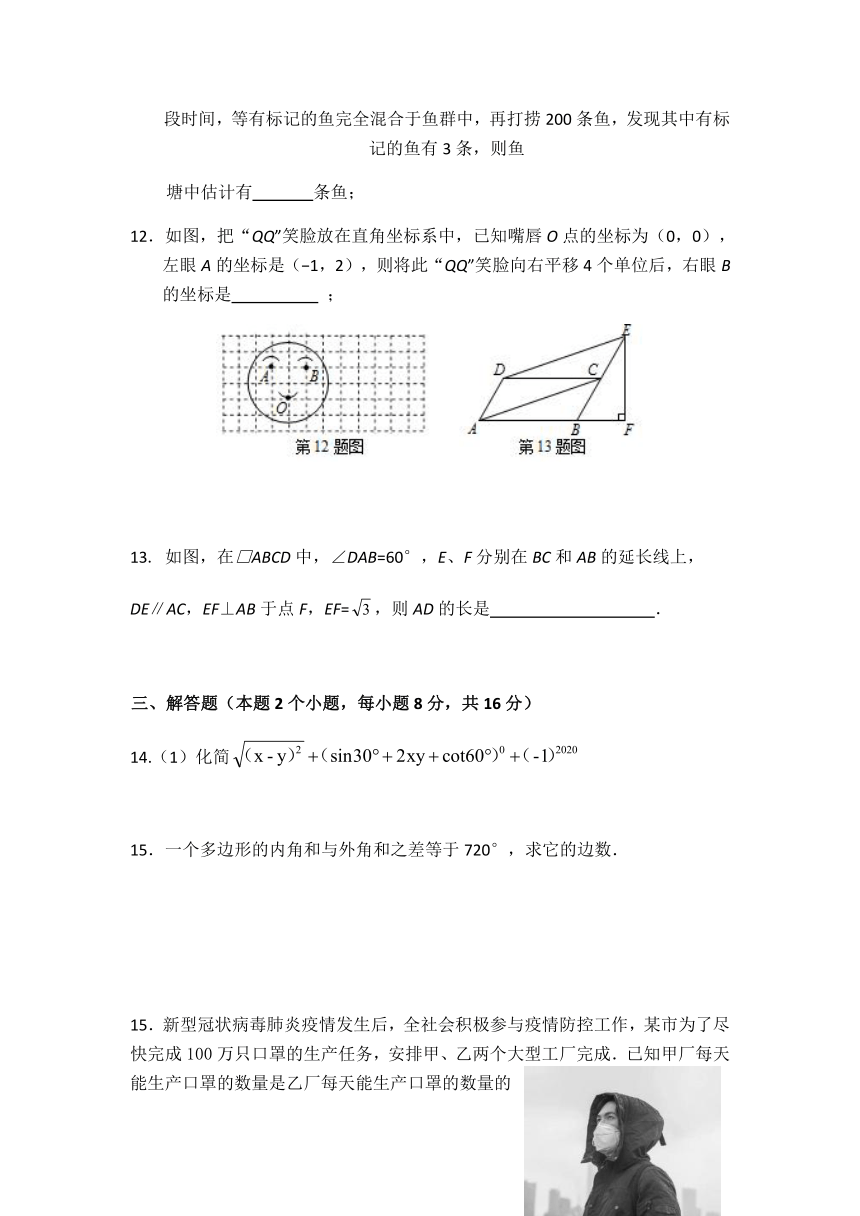
12.如图,把“QQ”笑脸放在直角坐标系中,已知嘴唇O点的坐标为(0,0),左眼A的坐标是(?1,2),则将此“QQ”笑脸向右平移4个单位后,右眼B的坐标是
;
13.
如图,在□ABCD中,∠DAB=60°,E、F分别在BC和AB的延长线上,
DE∥AC,EF⊥AB于点F,EF=,则AD的长是
.
三、解答题(本题2个小题,每小题8分,共16分)
14.(1)化简
15.一个多边形的内角和与外角和之差等于720°,求它的边数.
15.新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
四、解答题(本题3个小题,每小题8分,共24分)
16.某网店专售一款电动牙刷,其成本为20
元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)请求出y
与x
的函数关系式;
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出200元捐赠给武汉,为了保证捐款后每天剩余利润不低于550
元,如何确定该款电动牙刷的销售单价?
17.如图,在△ABC中,已知AD⊥BC,∠C=60°,DE是AC边的中线,且DE=1,请你求AD的长.
18.在学校开展的综合实践活动中,要求学生每人交一件作品.现从该校800名学生作品中抽取50件作品的成绩(单位:分)作样本分析,得出如下不完整的频数统计表如下:
(1)求x,y的值;
(2)若得分不低于80分为优秀,请问该校综合实践活动成绩优秀的学生约多少人?
五、解答题(本题2个小题,每小题10分,共20分)
19.某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人的积极性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的函数图像为折线OA-AB-BC,如图所示.
(1)求工人一天加工费不超过20个时每个零件的加工费.
(2)求40≤x≤60时y与x的函数关系式.
(3)小王两天一共加工了60个零件,共得到加工费220元,在这两天中,小王第一天加工的零件不足20个,求小王第一天加工零件的个数.
20.如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE
(1)若正方形ABCD的边长为8,BE=6,求EF的长?
(2)求证:AE=EC+CD.
六、解答题(本题12分)
21.某数学兴趣小组开展了一次课外活动,过程如下:如图,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点E,另一边交BC的延长线于点F.
(1)求证:DE=DF;
(2)如图,小明在图①的基础上做∠EDF的平分线DP交BC于点P,连接PE,他发现PE和PF存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点E,另一边交BC的延长线于点F,仍作∠EDF的平分线DP交BC延长线于点P,连接PE,若AB:AE=3:4,请帮小明算出△DPE的面积.
长沙2020年上学期考试八年级数学试卷模拟2
参考答案及评分标准
题号
1
2
3
4
5
6
7
8
答案
C
B
C
D
A
C
A
B
一、(本题共8个小题,每小题4分,满分32分
二、(本题5个小题,每小题4分,满分20分)
9.50°;10.2x-2;11.2000.;12.(5,2);13.1.
三、解答题(本题2个小题,每小题6分,共12分)
14.解:设这个多边形的边数为n,
1分
由已知条件得:
3分
解得:
5分
所以这个多边形的边数为8.
6分
15.
解:由已知可知,△ADC为等边三角形,
即,AD=AC=DC=2
,
所以,
2分
所以,
4分
因此,菱形各顶点的坐标分别为:,,,
6分
四、解答题(本题3个小题,每小题8分,共24分)
16.解:(1)设正比例函数的表达式为y=k1x.
因为它的图象经过点P(1,2),
所以2=k1,
解得k1=-2.
所以这个正比例函数的表达式为
4分
(2)设所求的一次函数的表达式为y=k2x+b.
因为它的图象经过点P(1,2),Q(0,3),
所以,
解得,
所以这个一次函数的表达式为.
8分
17.解:∵AD⊥BC于点D
∴
1分
在Rt△ADC中,
∵DE是AC边的中线
∴
又DE=1
∴
AC=2
3分
∵∠ACD=60°,
∴∠DAC=30°
5分
∴
6分
∴
8分
18.
解:(1)或;
2分
或;
4分
(2)
∵在抽取的50人中不低于80分的频率为0.78,
5分
∴
(人)
7分
答:该校综合实践活动成绩优秀的学生约624人.
8分
五、解答题(本题2个小题,每小题10分,共20分)
19.解:(1)由图象可知,当0≤x≤20时,每个零件的加工费为60÷20=3元,
即工人一天加工零件不超过20个时,每个零件的加工费为3元.
2分
(2)当40≤x≤60时,设y与x的函数关系式为y=kx+b,
将B(40,140),C(60,240)代入,得
,解得
∴y与x的函数关系式为y=5x-60(40≤x≤60).
6分
(3)设小王第一天加工零件的个数为a,则第二天加工零件的个数为(60-a),
∵
小王第一天加工的零件不足20个,小王两天一共加工了60个零件。
∴小王第二天加工的零件不足60个,超过40个.
由(2)知,第二天加工零件的加工费为5(60-a)-60.
∴5(60-a)-60=220-3a,解得,a
=10.
∴小王第一天加工零件10个.
10分
20.
解:(1)∵四边形ABCD是正方形,
∴AD=CD=BC,∠D=∠C=90°.
∵BC=8,BE=6,
∴EC=2.
∵F是CD的中点,∴DF=CF=4.
在Rt△EFC中,由勾股定理得
4分
(2)证明:过F作FH⊥AE于H.
5分
∵AF平分∠DAE,∠D=90°,FH⊥AE.
∴FH=FD,
在Rt△AHF与Rt△ADF中,
∵AF为公共边,FH=FD.
∴△AHF≌△ADF(HL).
∴AH=AD,HF=DF.
7分
又∵DF=FC=FH,FE为公共边,
∴Rt△FHE≌Rt△FCE.
∴HE=CE.
9分
∵AE=AH+HE,AH=AD=CD,HE=CE,
∴AE=EC+CD.
10分
六、(本题满分12分)
21.(1)证明:∵四边形ABCD是正方形
∴DA=DC,∠DAE=∠DCF=90°
∵∠PDQ=90°
∴
∠ADE+∠EDC=90°
∵∠CDF+∠EDC=90°
∴∠ADE=∠CDF
在△ADE与△CDF中
∵
∴△ADE≌△CDF
(ASA)
∴DE=DF
4分
(2)解:PE=PF.
证明如下:
∵
DP是∠EDF的平分线
∴∠PDE=∠PDF
在△PDE与△PDF中
∵
∴△PDE≌△PDF
(SAS)
∴PE=PF
8分
(3)解:∵AB:AE=3:4,AB=6
∴AE=8,BE=2,
由(1)知:△ADE≌△CDF
则AE=CF=8
由(2)知:△PDE≌△PDF,PE=PF
设CP=x,则PE=PF=CF-CP=8-x
在Rt△PEB中,BE=2,BP=6+x,PE=8-x
由勾股定理得:
解得:
∴
∴△DPE的面积为:
.
12分
数
学
(模拟试卷2)
时量:120分钟
总分:150分
选择题(本题共10个小题,每小题4分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填在相应的表格内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.英国作家奥斯森有言“The
best
gift
that
a
tree
is
a
godsend”,总所周知,树林给我们创造了无限的价值。在长白山,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,请问小鸟至少飞行
A.4米
B.8米
C.10米
D.12米
2.在□ABCD中,下列结论一定正确的是
A.AC⊥BD
B.∠A+∠B=180°
C.AB=AD
D.∠A≠∠C
3.若x<2,化简
的正确结果是
A.-1
B.1
C.2x-5
D.5-2x
4.李老师对本班40名学生的一次数学测试成绩作了统计,列出如下的统计表,则本班这次数学测试中A等的人数是
A.16
B.14
C.4
D.6
5.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的
A.测量对角线是否相互平分
B.
测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.
测量对角线是否相等
6.下列函数中,y随x的增大而减少的函数是
A.y=2x+4
B.y=?2+4x
C.y=?2x+8
D.y=2x
7.点A(m,1)在函数y=3x的图象上,则m的值是
A.
B.1
C.2
D.3
8.如图,在□ABCD中,∠BAD=60°,且它的平分线与BC的延长线交于点E,与DC交于点F,又点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为
A.
8
B.
C.
4
D.
二、填空题(本题5个小题,每小题4分,共20分)
9.把分母有理化后得到的最简答案为
;
10.已知一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(0,?2)和点B(1,0),则y=
;
11.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘.经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中有标记的鱼有3条,则鱼
塘中估计有
条鱼;
12.如图,把“QQ”笑脸放在直角坐标系中,已知嘴唇O点的坐标为(0,0),左眼A的坐标是(?1,2),则将此“QQ”笑脸向右平移4个单位后,右眼B的坐标是
;
13.
如图,在□ABCD中,∠DAB=60°,E、F分别在BC和AB的延长线上,
DE∥AC,EF⊥AB于点F,EF=,则AD的长是
.
三、解答题(本题2个小题,每小题8分,共16分)
14.(1)化简
15.一个多边形的内角和与外角和之差等于720°,求它的边数.
15.新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
四、解答题(本题3个小题,每小题8分,共24分)
16.某网店专售一款电动牙刷,其成本为20
元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)请求出y
与x
的函数关系式;
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出200元捐赠给武汉,为了保证捐款后每天剩余利润不低于550
元,如何确定该款电动牙刷的销售单价?
17.如图,在△ABC中,已知AD⊥BC,∠C=60°,DE是AC边的中线,且DE=1,请你求AD的长.
18.在学校开展的综合实践活动中,要求学生每人交一件作品.现从该校800名学生作品中抽取50件作品的成绩(单位:分)作样本分析,得出如下不完整的频数统计表如下:
(1)求x,y的值;
(2)若得分不低于80分为优秀,请问该校综合实践活动成绩优秀的学生约多少人?
五、解答题(本题2个小题,每小题10分,共20分)
19.某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人的积极性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的函数图像为折线OA-AB-BC,如图所示.
(1)求工人一天加工费不超过20个时每个零件的加工费.
(2)求40≤x≤60时y与x的函数关系式.
(3)小王两天一共加工了60个零件,共得到加工费220元,在这两天中,小王第一天加工的零件不足20个,求小王第一天加工零件的个数.
20.如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE
(1)若正方形ABCD的边长为8,BE=6,求EF的长?
(2)求证:AE=EC+CD.
六、解答题(本题12分)
21.某数学兴趣小组开展了一次课外活动,过程如下:如图,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点E,另一边交BC的延长线于点F.
(1)求证:DE=DF;
(2)如图,小明在图①的基础上做∠EDF的平分线DP交BC于点P,连接PE,他发现PE和PF存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点E,另一边交BC的延长线于点F,仍作∠EDF的平分线DP交BC延长线于点P,连接PE,若AB:AE=3:4,请帮小明算出△DPE的面积.
长沙2020年上学期考试八年级数学试卷模拟2
参考答案及评分标准
题号
1
2
3
4
5
6
7
8
答案
C
B
C
D
A
C
A
B
一、(本题共8个小题,每小题4分,满分32分
二、(本题5个小题,每小题4分,满分20分)
9.50°;10.2x-2;11.2000.;12.(5,2);13.1.
三、解答题(本题2个小题,每小题6分,共12分)
14.解:设这个多边形的边数为n,
1分
由已知条件得:
3分
解得:
5分
所以这个多边形的边数为8.
6分
15.
解:由已知可知,△ADC为等边三角形,
即,AD=AC=DC=2
,
所以,
2分
所以,
4分
因此,菱形各顶点的坐标分别为:,,,
6分
四、解答题(本题3个小题,每小题8分,共24分)
16.解:(1)设正比例函数的表达式为y=k1x.
因为它的图象经过点P(1,2),
所以2=k1,
解得k1=-2.
所以这个正比例函数的表达式为
4分
(2)设所求的一次函数的表达式为y=k2x+b.
因为它的图象经过点P(1,2),Q(0,3),
所以,
解得,
所以这个一次函数的表达式为.
8分
17.解:∵AD⊥BC于点D
∴
1分
在Rt△ADC中,
∵DE是AC边的中线
∴
又DE=1
∴
AC=2
3分
∵∠ACD=60°,
∴∠DAC=30°
5分
∴
6分
∴
8分
18.
解:(1)或;
2分
或;
4分
(2)
∵在抽取的50人中不低于80分的频率为0.78,
5分
∴
(人)
7分
答:该校综合实践活动成绩优秀的学生约624人.
8分
五、解答题(本题2个小题,每小题10分,共20分)
19.解:(1)由图象可知,当0≤x≤20时,每个零件的加工费为60÷20=3元,
即工人一天加工零件不超过20个时,每个零件的加工费为3元.
2分
(2)当40≤x≤60时,设y与x的函数关系式为y=kx+b,
将B(40,140),C(60,240)代入,得
,解得
∴y与x的函数关系式为y=5x-60(40≤x≤60).
6分
(3)设小王第一天加工零件的个数为a,则第二天加工零件的个数为(60-a),
∵
小王第一天加工的零件不足20个,小王两天一共加工了60个零件。
∴小王第二天加工的零件不足60个,超过40个.
由(2)知,第二天加工零件的加工费为5(60-a)-60.
∴5(60-a)-60=220-3a,解得,a
=10.
∴小王第一天加工零件10个.
10分
20.
解:(1)∵四边形ABCD是正方形,
∴AD=CD=BC,∠D=∠C=90°.
∵BC=8,BE=6,
∴EC=2.
∵F是CD的中点,∴DF=CF=4.
在Rt△EFC中,由勾股定理得
4分
(2)证明:过F作FH⊥AE于H.
5分
∵AF平分∠DAE,∠D=90°,FH⊥AE.
∴FH=FD,
在Rt△AHF与Rt△ADF中,
∵AF为公共边,FH=FD.
∴△AHF≌△ADF(HL).
∴AH=AD,HF=DF.
7分
又∵DF=FC=FH,FE为公共边,
∴Rt△FHE≌Rt△FCE.
∴HE=CE.
9分
∵AE=AH+HE,AH=AD=CD,HE=CE,
∴AE=EC+CD.
10分
六、(本题满分12分)
21.(1)证明:∵四边形ABCD是正方形
∴DA=DC,∠DAE=∠DCF=90°
∵∠PDQ=90°
∴
∠ADE+∠EDC=90°
∵∠CDF+∠EDC=90°
∴∠ADE=∠CDF
在△ADE与△CDF中
∵
∴△ADE≌△CDF
(ASA)
∴DE=DF
4分
(2)解:PE=PF.
证明如下:
∵
DP是∠EDF的平分线
∴∠PDE=∠PDF
在△PDE与△PDF中
∵
∴△PDE≌△PDF
(SAS)
∴PE=PF
8分
(3)解:∵AB:AE=3:4,AB=6
∴AE=8,BE=2,
由(1)知:△ADE≌△CDF
则AE=CF=8
由(2)知:△PDE≌△PDF,PE=PF
设CP=x,则PE=PF=CF-CP=8-x
在Rt△PEB中,BE=2,BP=6+x,PE=8-x
由勾股定理得:
解得:
∴
∴△DPE的面积为:
.
12分
同课章节目录
