人教版八年级上册数学:11.1.1三角形的边 同步练习 (含答案)
文档属性
| 名称 | 人教版八年级上册数学:11.1.1三角形的边 同步练习 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 141.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 03:36:50 | ||
图片预览


文档简介
人教版八年级上册数学11.1.1三角形的边
同步练习
一、单选题
1.以下列各组线段为边,能组成三角形的是(
)
A.2cm、2cm、4cm
B.2cm、6cm、3cm
C.8cm、6cm、3cm
D.11cm、4cm、6cm
2.已知三角形三边长分别为2,x,5,若x为整数,则这样的三角形个数为( )
A.2
B.3
C.4
D.5
3.一个三角形的两边长分别为3和4,且第三边长为整数,这样的三角形的周长最大值是(
)
A.11
B.12
C.13
D.14
4.如图,已知P是△ABC内任一点,
AB=12,BC=10,AC=6,则
PA+PB+PC的值一定大于(
)
A.14
B.15
C.16
D.28
5.如图,为估计南开中学桃李湖岸边两点之间的距离,小华在湖的一侧选取一点,测到米,米,则间的距离可能是(
)
A.5
米
B.15
米
C.25
米
D.30
米
6.图中的三角形被木板遮住了一部分,这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
7.以长分别为3,
4,
5,
6的四段木棒为边摆三角形,可摆出几种不同的三角形(
)
A.1种
B.2种
C.3种
D.4种
8.有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长(
)
A.最小值是11
B.最小值是12
C.最大值是14
D.最大值是15
9.已知的三边长分别为,且那么(
)
A.
B.
C.
D.
二、填空题
10.三角形的两边长分别是3和7,则其第三边x的范围为______________.
11.如图,图中以BC为边的三角形的个数为_____.
12.若三条长度分别为(为正整数)的线段可以围城一个三角形,则的值可能为__________.
13.已知a,b,c是△ABC的三边长,a,b满足|a﹣7|+(b﹣1)2=0,c为奇数,则c=_____.
14.已知a,b,c是三角形的三边长,化简:|a-b+c|-|b-a-c|=__________.
15.用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余、重叠和折断,则能摆出不同的三角形的个数是
_______个.
16.不能构成三角形的三条整数长度的线段的长度和的最小值为1+1+2=4;若四条整数长度的线段中,任意三条不能构成三角形,则该四条线段的长度和的最小值为1+1+2+3=7;……,依此规律,若八条整数长度的线段中,任意三条不能构成三角形,则该八条线段的长度和的最小值为________.
三、解答题
17.如图,在△ABC中,D,E是BC,AC上的点,连接BE,AD,交于点F,问:
(1)图中有多少个三角形?并把它们表示出来.
(2)△BDF的三个顶点是什么?三条边是什么?
(3)以AB为边的三角形有哪些?
(4)以F为顶点的三角形有哪些?
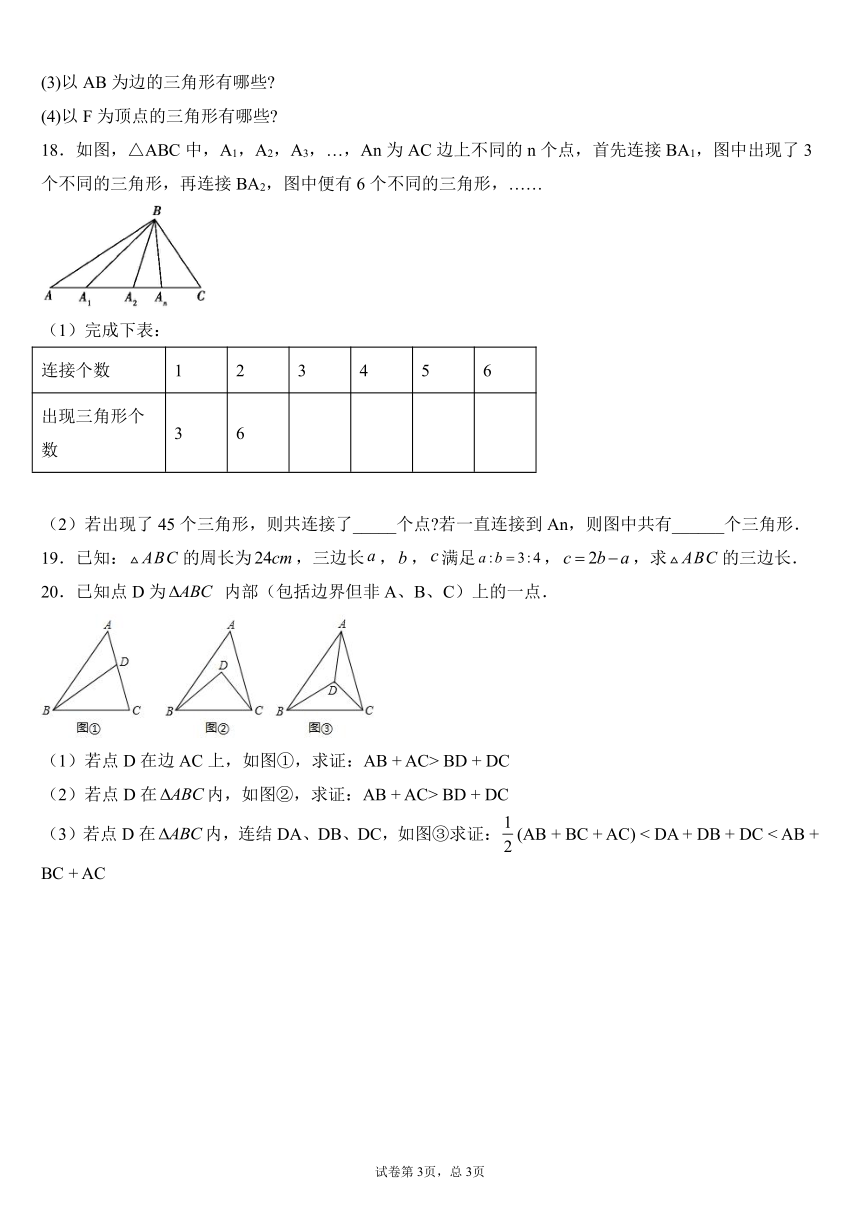
18.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形,……
(1)完成下表:
连接个数
1
2
3
4
5
6
出现三角形个数
3
6
(2)若出现了45个三角形,则共连接了_____个点?若一直连接到An,则图中共有______个三角形.
19.已知:的周长为,三边长,,满足,,求的三边长.
20.已知点D为
内部(包括边界但非A、B、C)上的一点.
(1)若点D在边AC上,如图①,求证:AB
+
AC>
BD
+
DC
(2)若点D在内,如图②,求证:AB
+
AC>
BD
+
DC
(3)若点D在内,连结DA、DB、DC,如图③求证:(AB
+
BC
+
AC)
<
DA
+
DB
+
DC
<
AB
+
BC
+
AC
试卷第2页,总3页
试卷第1页,总3页
答案
1.C
2.B
3.C
4.A、
5.B
6.D
7.D
8.D
9.D
10.4<x<10
11.4.
12.6cm,7
cm,8
cm,9
cm,10
cm.
13.7
14.0
15.3
16..
17.解:(1)8个:△ABC,△ABF,△ABE,△ABD,△BDF,△AEF,△ACD,△BCE;
(2)三个顶点:B,D,F;三条边:BD,BF,DF;
(3)△ABC,△ABF,△ABD,△ABE;
(4)△ABF,△BDF,△AEF.
18.解:(1)由图形可得:数三角形的个数,其实就是数AC上线段的个数.
所以当1个分点时,有三角形数为;
2个分点时,有三角形数为;
3个分点时,有;
4个分点时,有;
5个分点时,有;
6个分点时,有;
(2)若出现45=1+2+3+4+5+6+7+8+9个三角形,根据上述规律,则有8个分点;
若有个分点,则有.
19解:∵三边长,,满足,
∴设a=3x
cm,b=4x
cm,则=5x
cm,
∵△ABC的周长为,
∴3x+4x+5x=24,解得:x=2,
∴a=6cm,b=8cm,c=10cm.
20.解:(1)∵
AB
+
AD>BD
∴
AB
+
AD
+DC
>
BD
+DC
∴
AB
+
AC>BD
+DC
(2)延长BD交AC于E
∵
AB
+
AE
>
BD
+
DE①
DE
+EC
>DC
②
∴由①+②,得AB
+
AE+
DE
+EC>BD
+
DE+
DC
整理,得AB+AC>BD+DC
(3)∵
AD+BD>AB
①
BD+DC>BC
②
AD+DC>AC③
∴
把①
+
②
+③
得
AD+BD+BD+DC+
AD+DC>AB+BC+AC
整理,得
AD+DB+DC>(AB+BC+AC)
又∵
由上面(2)式得到:
DB+DA①
DB+DC②
DA+DC∴
把①
+
②
+③
得DB+DA+
DB+DC+
DA+DC<AC+BC+
AB+AC+
AB+BC
整理得
DA+DB+DC∴(AB
+
BC
+
AC)
<
DA
+
DB
+
DC
<
AB
+
BC
+
AC
同步练习
一、单选题
1.以下列各组线段为边,能组成三角形的是(
)
A.2cm、2cm、4cm
B.2cm、6cm、3cm
C.8cm、6cm、3cm
D.11cm、4cm、6cm
2.已知三角形三边长分别为2,x,5,若x为整数,则这样的三角形个数为( )
A.2
B.3
C.4
D.5
3.一个三角形的两边长分别为3和4,且第三边长为整数,这样的三角形的周长最大值是(
)
A.11
B.12
C.13
D.14
4.如图,已知P是△ABC内任一点,
AB=12,BC=10,AC=6,则
PA+PB+PC的值一定大于(
)
A.14
B.15
C.16
D.28
5.如图,为估计南开中学桃李湖岸边两点之间的距离,小华在湖的一侧选取一点,测到米,米,则间的距离可能是(
)
A.5
米
B.15
米
C.25
米
D.30
米
6.图中的三角形被木板遮住了一部分,这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
7.以长分别为3,
4,
5,
6的四段木棒为边摆三角形,可摆出几种不同的三角形(
)
A.1种
B.2种
C.3种
D.4种
8.有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长(
)
A.最小值是11
B.最小值是12
C.最大值是14
D.最大值是15
9.已知的三边长分别为,且那么(
)
A.
B.
C.
D.
二、填空题
10.三角形的两边长分别是3和7,则其第三边x的范围为______________.
11.如图,图中以BC为边的三角形的个数为_____.
12.若三条长度分别为(为正整数)的线段可以围城一个三角形,则的值可能为__________.
13.已知a,b,c是△ABC的三边长,a,b满足|a﹣7|+(b﹣1)2=0,c为奇数,则c=_____.
14.已知a,b,c是三角形的三边长,化简:|a-b+c|-|b-a-c|=__________.
15.用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余、重叠和折断,则能摆出不同的三角形的个数是
_______个.
16.不能构成三角形的三条整数长度的线段的长度和的最小值为1+1+2=4;若四条整数长度的线段中,任意三条不能构成三角形,则该四条线段的长度和的最小值为1+1+2+3=7;……,依此规律,若八条整数长度的线段中,任意三条不能构成三角形,则该八条线段的长度和的最小值为________.
三、解答题
17.如图,在△ABC中,D,E是BC,AC上的点,连接BE,AD,交于点F,问:
(1)图中有多少个三角形?并把它们表示出来.
(2)△BDF的三个顶点是什么?三条边是什么?
(3)以AB为边的三角形有哪些?
(4)以F为顶点的三角形有哪些?
18.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形,……
(1)完成下表:
连接个数
1
2
3
4
5
6
出现三角形个数
3
6
(2)若出现了45个三角形,则共连接了_____个点?若一直连接到An,则图中共有______个三角形.
19.已知:的周长为,三边长,,满足,,求的三边长.
20.已知点D为
内部(包括边界但非A、B、C)上的一点.
(1)若点D在边AC上,如图①,求证:AB
+
AC>
BD
+
DC
(2)若点D在内,如图②,求证:AB
+
AC>
BD
+
DC
(3)若点D在内,连结DA、DB、DC,如图③求证:(AB
+
BC
+
AC)
<
DA
+
DB
+
DC
<
AB
+
BC
+
AC
试卷第2页,总3页
试卷第1页,总3页
答案
1.C
2.B
3.C
4.A、
5.B
6.D
7.D
8.D
9.D
10.4<x<10
11.4.
12.6cm,7
cm,8
cm,9
cm,10
cm.
13.7
14.0
15.3
16..
17.解:(1)8个:△ABC,△ABF,△ABE,△ABD,△BDF,△AEF,△ACD,△BCE;
(2)三个顶点:B,D,F;三条边:BD,BF,DF;
(3)△ABC,△ABF,△ABD,△ABE;
(4)△ABF,△BDF,△AEF.
18.解:(1)由图形可得:数三角形的个数,其实就是数AC上线段的个数.
所以当1个分点时,有三角形数为;
2个分点时,有三角形数为;
3个分点时,有;
4个分点时,有;
5个分点时,有;
6个分点时,有;
(2)若出现45=1+2+3+4+5+6+7+8+9个三角形,根据上述规律,则有8个分点;
若有个分点,则有.
19解:∵三边长,,满足,
∴设a=3x
cm,b=4x
cm,则=5x
cm,
∵△ABC的周长为,
∴3x+4x+5x=24,解得:x=2,
∴a=6cm,b=8cm,c=10cm.
20.解:(1)∵
AB
+
AD>BD
∴
AB
+
AD
+DC
>
BD
+DC
∴
AB
+
AC>BD
+DC
(2)延长BD交AC于E
∵
AB
+
AE
>
BD
+
DE①
DE
+EC
>DC
②
∴由①+②,得AB
+
AE+
DE
+EC>BD
+
DE+
DC
整理,得AB+AC>BD+DC
(3)∵
AD+BD>AB
①
BD+DC>BC
②
AD+DC>AC③
∴
把①
+
②
+③
得
AD+BD+BD+DC+
AD+DC>AB+BC+AC
整理,得
AD+DB+DC>(AB+BC+AC)
又∵
由上面(2)式得到:
DB+DA
DB+DC
DA+DC
把①
+
②
+③
得DB+DA+
DB+DC+
DA+DC<AC+BC+
AB+AC+
AB+BC
整理得
DA+DB+DC
+
BC
+
AC)
<
DA
+
DB
+
DC
<
AB
+
BC
+
AC
