人教版八年级上册数学11.2.1 三角形的内角 同步练习(word版含答案)
文档属性
| 名称 | 人教版八年级上册数学11.2.1 三角形的内角 同步练习(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 238.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 00:00:00 | ||
图片预览


文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
人教版八年级上册数学11.2.1
三角形的内角
练习
一、单选题
1.已知△ABC的三个内角∠A,∠B,∠C满足关系式∠B+∠C=3∠A,则此三角形( )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
2.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65°
B.55°
C.45°
D.35°
3.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5°
B.8°
C.10°
D.15°
4.在下列条件中①∠A+∠B=∠C
②∠A﹕∠B﹕∠C=1﹕2﹕3
③∠A=∠B=∠C
④∠A=∠B=2∠C
⑤∠A=∠B=∠C
中能确定△ABC为直角三角形的条件有(
).
A.2个
B.3个
C.4个
D.5个
5.一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是(
)
A.150°
B.180°
C.135°
D.不能确定
6.如图,在中,是边上的高,,分别是,的角平分线,,,则的度数为(
)
A.5°
B.10°
C.15°
D.20°
7.在中,若一个内角等于另外两个角的差,则(
)
A.必有一个角等于
B.必有一个角等于
C.必有一个角等于
D.必有一个角等于
8.如图,乐乐将△ABC沿DE,EF分别翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO.若∠DOF=139°,则∠C=(
)
A.38°
B.39°
C.40°
D.41°
9.如图,在中,.与的平分线交于点,得;与的平分线相交于点,得,,与的平分线相交于点,得,则(
)
A.
B.
C.
D.
二、填空题
10.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC=_____度.
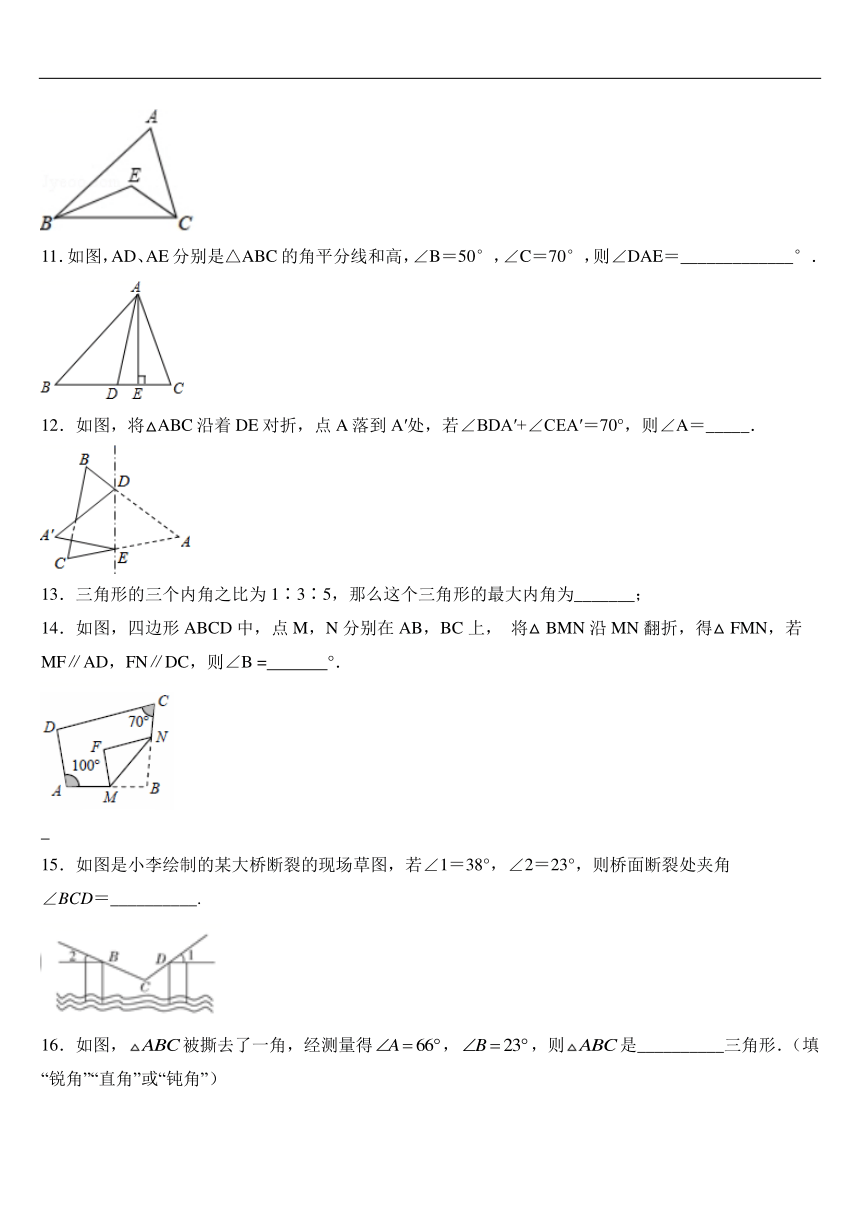
11.如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠DAE=_____________°.
12.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A=_____.
13.三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为_______;
14.如图,四边形ABCD中,点M,N分别在AB,BC上,
将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B
=
°.
15.如图是小李绘制的某大桥断裂的现场草图,若∠1=38°,∠2=23°,则桥面断裂处夹角∠BCD=__________.
16.如图,被撕去了一角,经测量得,,则是__________三角形.(填“锐角”“直角”或“钝角”)
三、解答题
17.如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC,
(1)求∠BAE的度数;(2)求∠DAE的度数.
18.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
19.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
20.如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有
个,以点O为交点的“8字型”有
个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
答案
1.A
2.B
3.C
4.C
5.A
6.A
7.D
8.D
9.C
10.122.
11.10
12.35°
13.100°
14.95
15.119°
16.钝角
17.(1)
∠BAE=30
°;(2)
∠EAD=20°.
18
解:在Rt△ABC中,,
∴,
又∵,
∴,
∴,
∴.
19.解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
20解:(1)在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①以线段AC为边的“8字型”有3个:
以点O为交点的“8字型”有4个:
②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAP=∠CAB,∠CDP=∠CDB,
∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B,
∴3∠P=∠B+2∠C.
试卷第6页,总6页
试卷第1页,总6页
答案第1页,总2页
人教版八年级上册数学11.2.1
三角形的内角
练习
一、单选题
1.已知△ABC的三个内角∠A,∠B,∠C满足关系式∠B+∠C=3∠A,则此三角形( )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
2.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65°
B.55°
C.45°
D.35°
3.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5°
B.8°
C.10°
D.15°
4.在下列条件中①∠A+∠B=∠C
②∠A﹕∠B﹕∠C=1﹕2﹕3
③∠A=∠B=∠C
④∠A=∠B=2∠C
⑤∠A=∠B=∠C
中能确定△ABC为直角三角形的条件有(
).
A.2个
B.3个
C.4个
D.5个
5.一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是(
)
A.150°
B.180°
C.135°
D.不能确定
6.如图,在中,是边上的高,,分别是,的角平分线,,,则的度数为(
)
A.5°
B.10°
C.15°
D.20°
7.在中,若一个内角等于另外两个角的差,则(
)
A.必有一个角等于
B.必有一个角等于
C.必有一个角等于
D.必有一个角等于
8.如图,乐乐将△ABC沿DE,EF分别翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO.若∠DOF=139°,则∠C=(
)
A.38°
B.39°
C.40°
D.41°
9.如图,在中,.与的平分线交于点,得;与的平分线相交于点,得,,与的平分线相交于点,得,则(
)
A.
B.
C.
D.
二、填空题
10.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC=_____度.
11.如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠DAE=_____________°.
12.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A=_____.
13.三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为_______;
14.如图,四边形ABCD中,点M,N分别在AB,BC上,
将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B
=
°.
15.如图是小李绘制的某大桥断裂的现场草图,若∠1=38°,∠2=23°,则桥面断裂处夹角∠BCD=__________.
16.如图,被撕去了一角,经测量得,,则是__________三角形.(填“锐角”“直角”或“钝角”)
三、解答题
17.如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC,
(1)求∠BAE的度数;(2)求∠DAE的度数.
18.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
19.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
20.如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有
个,以点O为交点的“8字型”有
个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
答案
1.A
2.B
3.C
4.C
5.A
6.A
7.D
8.D
9.C
10.122.
11.10
12.35°
13.100°
14.95
15.119°
16.钝角
17.(1)
∠BAE=30
°;(2)
∠EAD=20°.
18
解:在Rt△ABC中,,
∴,
又∵,
∴,
∴,
∴.
19.解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
20解:(1)在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①以线段AC为边的“8字型”有3个:
以点O为交点的“8字型”有4个:
②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAP=∠CAB,∠CDP=∠CDB,
∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B,
∴3∠P=∠B+2∠C.
试卷第6页,总6页
试卷第1页,总6页
答案第1页,总2页
