人教版八年级上册数学11.2.2 三角形的外角 同步练习(word版含答案)
文档属性
| 名称 | 人教版八年级上册数学11.2.2 三角形的外角 同步练习(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 07:50:29 | ||
图片预览


文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
人教版八年级上册数学11.2.2
三角形的外角
作业
一、单选题
1.在△ABC中,,与的外角度数如图所示,则x的值是
A.60
B.65
C.70
D.80
2.如图所示,∠的度数是(
)
A.10°
B.20°
C.30°
D.40°
3.如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为(
)
A.23°
B.92°
C.44°
D.46°
4.如图将直尺与含30°角的三角尺摆放在一起,若,则的度数是(
)
A.
B.
C.
D.
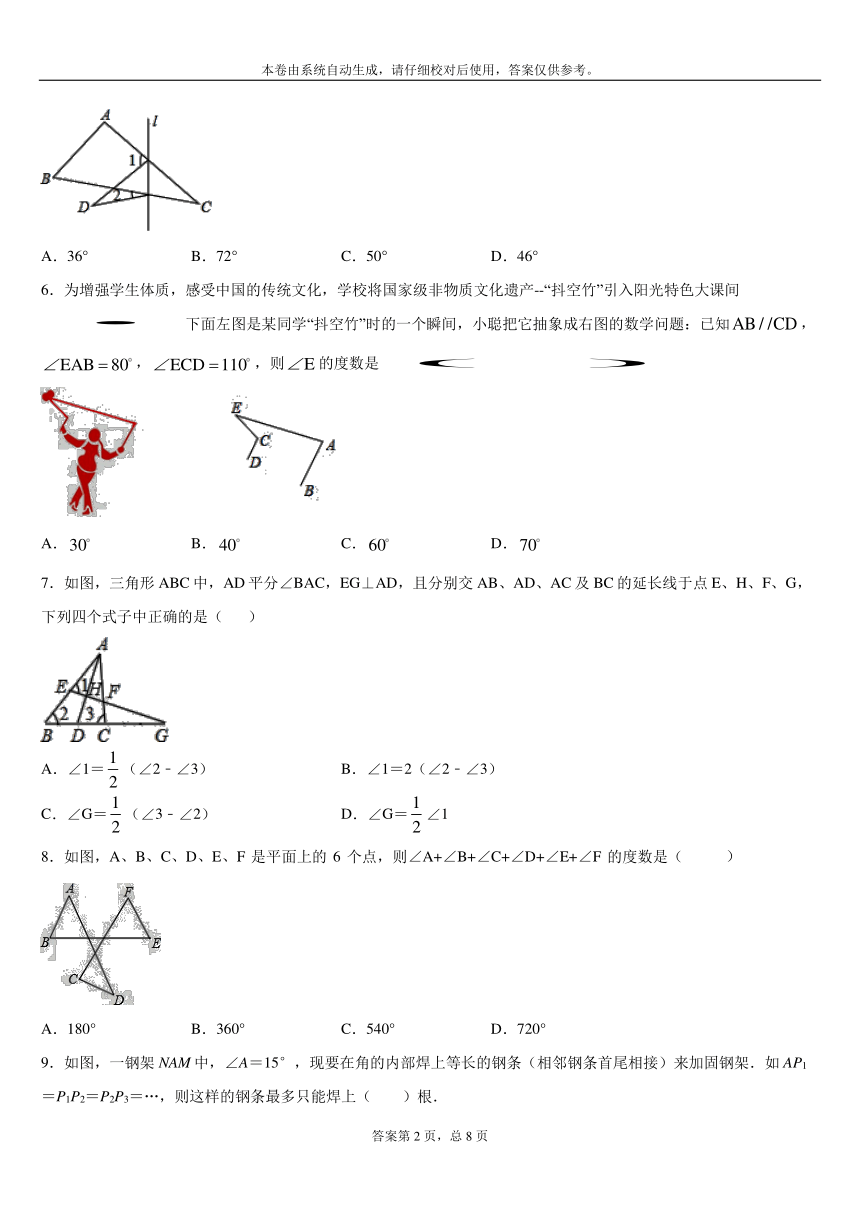
5.如图,在△ABC中,∠C=36°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是( )
A.36°
B.72°
C.50°
D.46°
6.为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产--“抖空竹”引入阳光特色大课间下面左图是某同学“抖空竹”时的一个瞬间,小聪把它抽象成右图的数学问题:已知,,,则的度数是
A.
B.
C.
D.
7.如图,三角形ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、AC及BC的延长线于点E、H、F、G,下列四个式子中正确的是(
)
A.∠1=(∠2﹣∠3)
B.∠1=2(∠2﹣∠3)
C.∠G=(∠3﹣∠2)
D.∠G=∠1
8.如图,A、B、C、D、E、F
是平面上的
6
个点,则∠A+∠B+∠C+∠D+∠E+∠F
的度数是(
)
A.180°
B.360°
C.540°
D.720°
9.如图,一钢架NAM中,∠A=15°,现要在角的内部焊上等长的钢条(相邻钢条首尾相接)来加固钢架.如AP1=P1P2=P2P3=…,则这样的钢条最多只能焊上( )根.
A.4
B.5
C.6
D.7
10.下面说法正确的个数有:(
)
①如果三角形三个内角的比是1:2:3,那么这个三角形是直角三角形;
②如果三角形的一个外角等于与它相邻的一个内角,则这个三角形是直角三角形;
③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;
④如果,那么是直角三角形;
⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;
⑥在中,若,则此三角形是直角三角形.
A.3个
B.4个
C.5个
D.6个
二、填空题
11.如图,若AB∥CD,∠C=60°,则∠A+∠E=_____度.
12.如果将一副三角板按如图方式叠放,那么∠1=_____.
13.中,,,点为延长线上一点,与的平分线相交于点,则的度数为__________.
14.如图,将一张三角形纸片
ABC
的一角折叠,使点
A
落在△ABC
外的
A'处,折痕为
DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么
α,β,γ
三个角的数量关系是__________
.
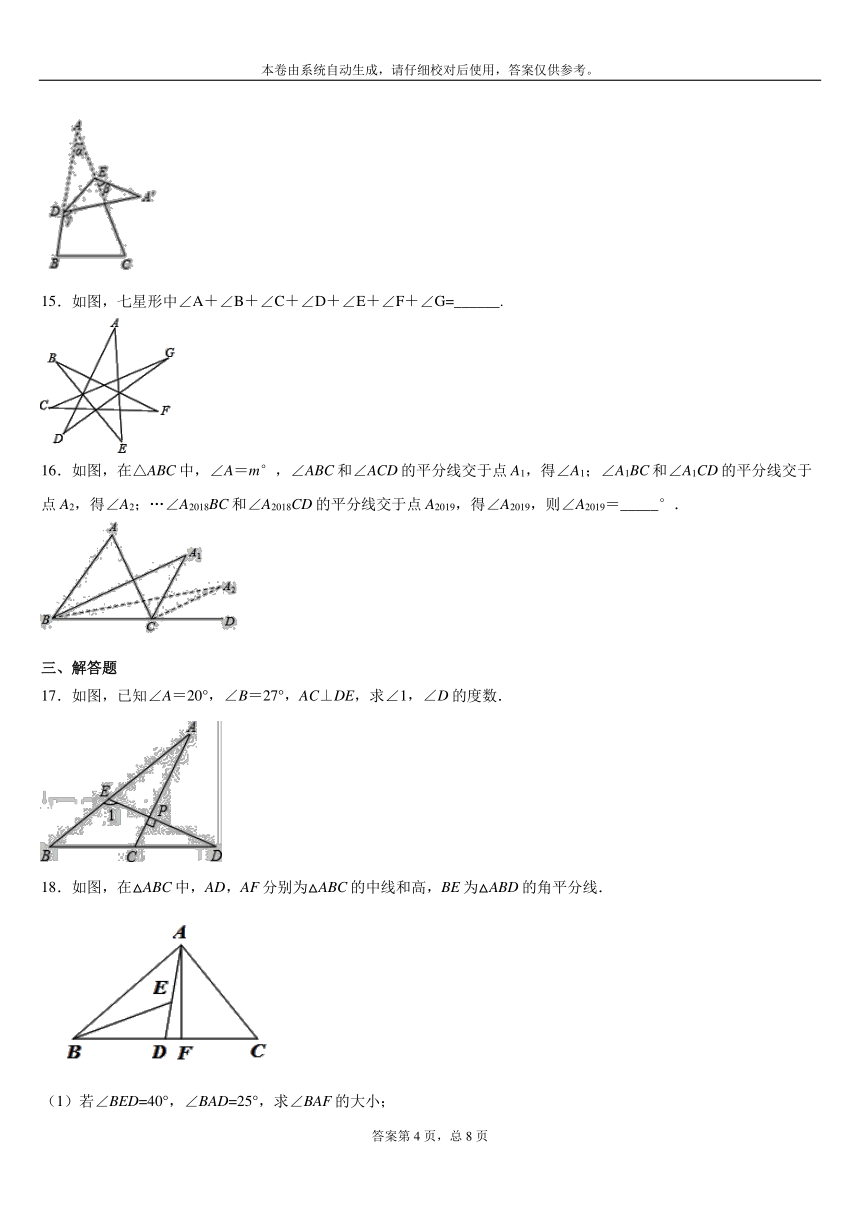
15.如图,七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G=______.
16.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2018BC和∠A2018CD的平分线交于点A2019,得∠A2019,则∠A2019=_____°.
三、解答题
17.如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.
18.如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
19.阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究一:如图1.在△ABC中,已知O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现.理由如下:
∵BO和CO分别是∠ABC与∠ACB的平分线,
∴,;
∴,
∴
(1)探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.
(2)探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?
20.直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
(问题探究)
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E=
;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
(变式拓展)
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是
.
答案
1.C
2.A
3.B
4.C
5.B
6.A
7.C
8.B
9.B
10.C
11.60
12.105°
13.15°
14.γ=2α+β.
15.180°
16.
17.43°
18.(1)60°;(2)8
19.解:(1),理由如下:
∵BO和CO分别是与的平分线,
∴,,
又∵是的一个外角,
∴,
∵是的一个外角,
∴
即
(2)∵BO与CO分别是∠CBD与∠BCE的平分线,
∴∠OBC=∠CBD,∠OCB=∠BCE
又∵∠CBD与∠BCE都是△ABC的外角,
∴∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠OBC=∠CBD=(∠A+∠ACB),∠OCB=∠BCE=(∠A+∠ABC),
∴∠BOC=180°-(∠OBC+∠OCB)
∴
20.解
(1)如图1,
∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°;
(2)将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°.
证明:如图2,
∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°.
证明:如图3,
∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°.
(4)如图4,
根据三角形中,一个内角的补角等于其余两个内角的和,
∴四边形FGBD中:∠FGB=∠B+∠D+∠F,
四边形ACGE中:∠CGE=∠A+∠C+∠E,
∵∠CGE=∠BGF=160°,
∴∠A+∠B+∠C+∠D+∠E+∠F=320°,
试卷第6页,总8页
答案第1页,总2页
人教版八年级上册数学11.2.2
三角形的外角
作业
一、单选题
1.在△ABC中,,与的外角度数如图所示,则x的值是
A.60
B.65
C.70
D.80
2.如图所示,∠的度数是(
)
A.10°
B.20°
C.30°
D.40°
3.如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为(
)
A.23°
B.92°
C.44°
D.46°
4.如图将直尺与含30°角的三角尺摆放在一起,若,则的度数是(
)
A.
B.
C.
D.
5.如图,在△ABC中,∠C=36°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是( )
A.36°
B.72°
C.50°
D.46°
6.为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产--“抖空竹”引入阳光特色大课间下面左图是某同学“抖空竹”时的一个瞬间,小聪把它抽象成右图的数学问题:已知,,,则的度数是
A.
B.
C.
D.
7.如图,三角形ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、AC及BC的延长线于点E、H、F、G,下列四个式子中正确的是(
)
A.∠1=(∠2﹣∠3)
B.∠1=2(∠2﹣∠3)
C.∠G=(∠3﹣∠2)
D.∠G=∠1
8.如图,A、B、C、D、E、F
是平面上的
6
个点,则∠A+∠B+∠C+∠D+∠E+∠F
的度数是(
)
A.180°
B.360°
C.540°
D.720°
9.如图,一钢架NAM中,∠A=15°,现要在角的内部焊上等长的钢条(相邻钢条首尾相接)来加固钢架.如AP1=P1P2=P2P3=…,则这样的钢条最多只能焊上( )根.
A.4
B.5
C.6
D.7
10.下面说法正确的个数有:(
)
①如果三角形三个内角的比是1:2:3,那么这个三角形是直角三角形;
②如果三角形的一个外角等于与它相邻的一个内角,则这个三角形是直角三角形;
③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;
④如果,那么是直角三角形;
⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;
⑥在中,若,则此三角形是直角三角形.
A.3个
B.4个
C.5个
D.6个
二、填空题
11.如图,若AB∥CD,∠C=60°,则∠A+∠E=_____度.
12.如果将一副三角板按如图方式叠放,那么∠1=_____.
13.中,,,点为延长线上一点,与的平分线相交于点,则的度数为__________.
14.如图,将一张三角形纸片
ABC
的一角折叠,使点
A
落在△ABC
外的
A'处,折痕为
DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么
α,β,γ
三个角的数量关系是__________
.
15.如图,七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G=______.
16.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2018BC和∠A2018CD的平分线交于点A2019,得∠A2019,则∠A2019=_____°.
三、解答题
17.如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.
18.如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
19.阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究一:如图1.在△ABC中,已知O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现.理由如下:
∵BO和CO分别是∠ABC与∠ACB的平分线,
∴,;
∴,
∴
(1)探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.
(2)探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?
20.直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
(问题探究)
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E=
;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
(变式拓展)
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是
.
答案
1.C
2.A
3.B
4.C
5.B
6.A
7.C
8.B
9.B
10.C
11.60
12.105°
13.15°
14.γ=2α+β.
15.180°
16.
17.43°
18.(1)60°;(2)8
19.解:(1),理由如下:
∵BO和CO分别是与的平分线,
∴,,
又∵是的一个外角,
∴,
∵是的一个外角,
∴
即
(2)∵BO与CO分别是∠CBD与∠BCE的平分线,
∴∠OBC=∠CBD,∠OCB=∠BCE
又∵∠CBD与∠BCE都是△ABC的外角,
∴∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠OBC=∠CBD=(∠A+∠ACB),∠OCB=∠BCE=(∠A+∠ABC),
∴∠BOC=180°-(∠OBC+∠OCB)
∴
20.解
(1)如图1,
∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°;
(2)将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°.
证明:如图2,
∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°.
证明:如图3,
∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°.
(4)如图4,
根据三角形中,一个内角的补角等于其余两个内角的和,
∴四边形FGBD中:∠FGB=∠B+∠D+∠F,
四边形ACGE中:∠CGE=∠A+∠C+∠E,
∵∠CGE=∠BGF=160°,
∴∠A+∠B+∠C+∠D+∠E+∠F=320°,
试卷第6页,总8页
答案第1页,总2页
