人教版八年级数学上册:11.3.2多边形的内角和能力提升卷 (word版,含答案)
文档属性
| 名称 | 人教版八年级数学上册:11.3.2多边形的内角和能力提升卷 (word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 174.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册
11.3.2多边形的内角和
能力提升卷
一、选择题(共10小题,3
10=30)
1.下列角度能成为某多边形内角和的是(
)
A.270°
B.550°
C.1800°
D.1200°
2.已知一个多边形的内角和是1
080°,则这个多边形是( )
A.五边形
B.六边形
C.七边形
D.八边形
3.若一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.8
B.9
C.10
D.11
4.从n边形的同一个顶点出发,分别连接这个顶点与其余顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6
B.7
C.8
D.9
5.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7
B.10
C.35
D.70
6.
如图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360°
B.540°
C.630°
D.720°
7.一个多边形切去一个角后,形成的另一个多边形的内角和为1
080°,那么原多边形的边数为( )
A.7
B.7或8
C.8或9
D.7或8或9
8.设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是(
)
A.a>b
B.a=b
C.a<b
D.b=a+180°
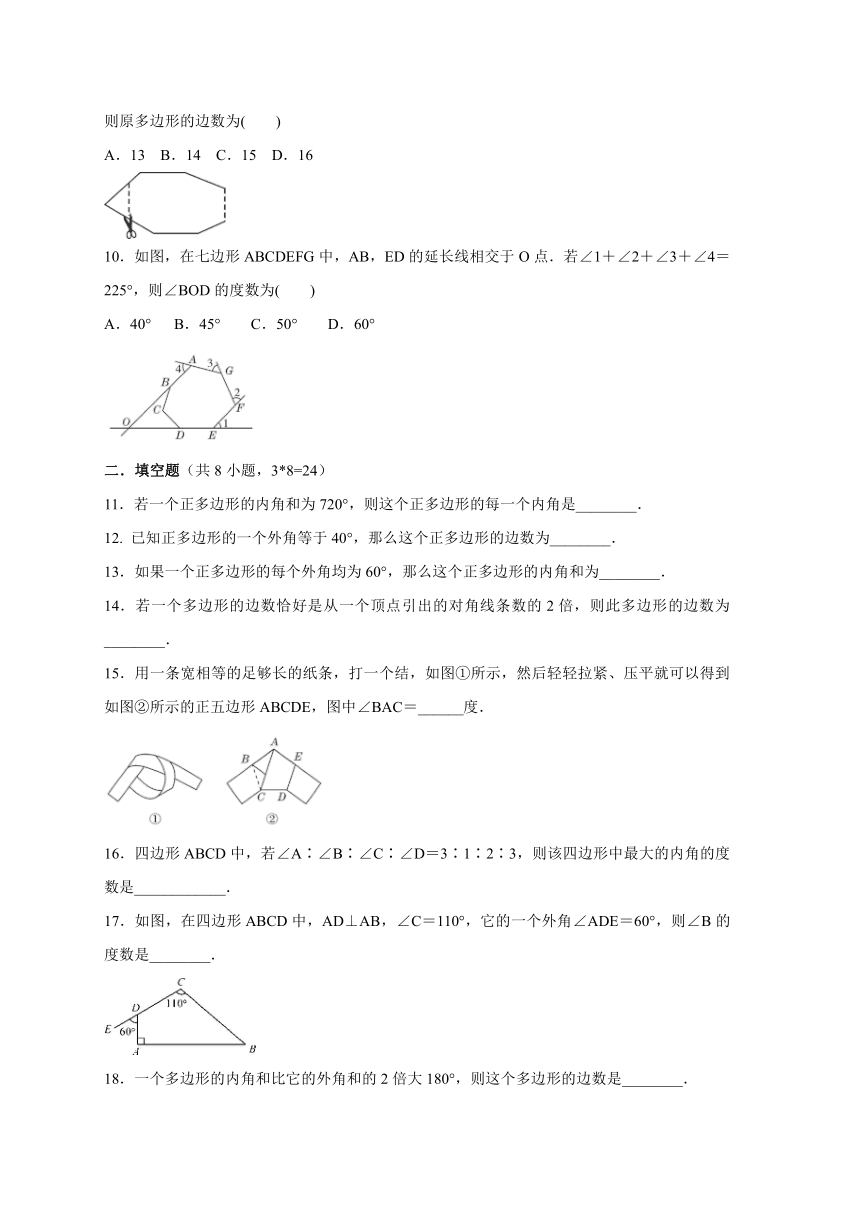
9.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
A.13
B.14
C.15
D.16
10.如图,在七边形ABCDEFG中,AB,ED的延长线相交于O点.若∠1+∠2+∠3+∠4=225°,则∠BOD的度数为( )
A.40°
B.45°
C.50°
D.60°
二.填空题(共8小题,3
8=24)
11.若一个正多边形的内角和为720°,则这个正多边形的每一个内角是________.
12.
已知正多边形的一个外角等于40°,那么这个正多边形的边数为________.
13.如果一个正多边形的每个外角均为60°,那么这个正多边形的内角和为________.
14.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,则此多边形的边数为________.
15.用一条宽相等的足够长的纸条,打一个结,如图①所示,然后轻轻拉紧、压平就可以得到如图②所示的正五边形ABCDE,图中∠BAC=______度.
16.四边形ABCD中,若∠A∶∠B∶∠C∶∠D=3∶1∶2∶3,则该四边形中最大的内角的度数是____________.
17.如图,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的度数是________.
18.一个多边形的内角和比它的外角和的2倍大180°,则这个多边形的边数是________.
三.解答题(共7小题,
46分)
19.(6分)
如图,五边形ABCDE是正五边形,若l1∥l2,求∠1-∠2的度数.
20.(6分)
如图在正五边形ABCDE中.
(1)求∠B的度数;
(2)连接AC,若∠BAC=∠BCA,求证:AC∥DE.
21.(6分)
已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
22.(6分)
如图,在四边形ABCD中,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
23.(6分)
如图,小明从点O出发,前进5m后向右转15°,再前进5m后又向右转15°,……这样一直下去,直到他第一次回到出发点O,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
24.(8分)
如图,在四边形ABCD中,若∠ABC和∠BCD的平分线交于点E,求∠BEC的度数.
25.(8分)
(1)如图①②,试探究∠1,∠2与∠3,∠4之间的数量关系;
(2)请你用文字描述上述关系;
参考答案
1-5CDACC
6-10CDBBB
11.
120°
12.
9
13.
720°
14.
6
15.
36
16.
120°
17.
100°
18.
7
19.
解:过点B作BF∥l1交DE于点F,则BF∥l1∥l2,
∴∠2=∠ABF,∠1+∠CBF=180°.
∵五边形ABCDE是正五边形,
∴∠ABC==108°.
∴∠1-∠2=180°-∠CBF-∠ABF=180°-(∠CBF+∠ABF)=180°-∠ABC=72°.
20.
解:(1)∠B=108°
(2)∵∠BCA=∠BAC,∠B=108°,
∴∠BCA==36°,∴∠ACD=72°,
∵∠D=∠B=108°,∴∠ACD+∠D=180°,
∴AC∥DE
21.
解:(1)甲对,乙不对.
∵θ=360°,∴(n-2)×180°=360°,
解得n=4,
∵θ=630°,∴(n-2)×180°=630°,
解得n=,
∵n为整数,∴θ不能取630°
(2)根据题意得(n-2)×180+360=(n+x-2)×180,
解得x=2
22.
解:∵BE∥AD,∠D=80°,
∠A=140°,∴∠BEC=∠D=80°,
∠ABE=180°-∠A=180°-140°=40°.
又∵BE平分∠ABC,∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
23.
解:(1)∵所经过的路线正好构成一个外角是15°的正多边形,
∴360÷15=24,24×5=120(m).
答:小明一共走了120米.
(2)
(24-2)×180°=3
960°.
答:这个多边形的内角和是3
960°.
24.
解:∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°.
∵∠ABC和∠BCD的平分线交于点E,
∴∠EBC=∠ABC,∠BCE=∠BCD.
∴∠E=180°-∠EBC-∠BCE=180°-(∠ABC+∠BCD)=180°-×140°=110°.
25.
解:(1)设∠1的邻补角为∠5,∠2的邻补角为∠6.
∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
11.3.2多边形的内角和
能力提升卷
一、选择题(共10小题,3
10=30)
1.下列角度能成为某多边形内角和的是(
)
A.270°
B.550°
C.1800°
D.1200°
2.已知一个多边形的内角和是1
080°,则这个多边形是( )
A.五边形
B.六边形
C.七边形
D.八边形
3.若一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.8
B.9
C.10
D.11
4.从n边形的同一个顶点出发,分别连接这个顶点与其余顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6
B.7
C.8
D.9
5.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7
B.10
C.35
D.70
6.
如图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360°
B.540°
C.630°
D.720°
7.一个多边形切去一个角后,形成的另一个多边形的内角和为1
080°,那么原多边形的边数为( )
A.7
B.7或8
C.8或9
D.7或8或9
8.设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是(
)
A.a>b
B.a=b
C.a<b
D.b=a+180°
9.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
A.13
B.14
C.15
D.16
10.如图,在七边形ABCDEFG中,AB,ED的延长线相交于O点.若∠1+∠2+∠3+∠4=225°,则∠BOD的度数为( )
A.40°
B.45°
C.50°
D.60°
二.填空题(共8小题,3
8=24)
11.若一个正多边形的内角和为720°,则这个正多边形的每一个内角是________.
12.
已知正多边形的一个外角等于40°,那么这个正多边形的边数为________.
13.如果一个正多边形的每个外角均为60°,那么这个正多边形的内角和为________.
14.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,则此多边形的边数为________.
15.用一条宽相等的足够长的纸条,打一个结,如图①所示,然后轻轻拉紧、压平就可以得到如图②所示的正五边形ABCDE,图中∠BAC=______度.
16.四边形ABCD中,若∠A∶∠B∶∠C∶∠D=3∶1∶2∶3,则该四边形中最大的内角的度数是____________.
17.如图,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的度数是________.
18.一个多边形的内角和比它的外角和的2倍大180°,则这个多边形的边数是________.
三.解答题(共7小题,
46分)
19.(6分)
如图,五边形ABCDE是正五边形,若l1∥l2,求∠1-∠2的度数.
20.(6分)
如图在正五边形ABCDE中.
(1)求∠B的度数;
(2)连接AC,若∠BAC=∠BCA,求证:AC∥DE.
21.(6分)
已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
22.(6分)
如图,在四边形ABCD中,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
23.(6分)
如图,小明从点O出发,前进5m后向右转15°,再前进5m后又向右转15°,……这样一直下去,直到他第一次回到出发点O,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
24.(8分)
如图,在四边形ABCD中,若∠ABC和∠BCD的平分线交于点E,求∠BEC的度数.
25.(8分)
(1)如图①②,试探究∠1,∠2与∠3,∠4之间的数量关系;
(2)请你用文字描述上述关系;
参考答案
1-5CDACC
6-10CDBBB
11.
120°
12.
9
13.
720°
14.
6
15.
36
16.
120°
17.
100°
18.
7
19.
解:过点B作BF∥l1交DE于点F,则BF∥l1∥l2,
∴∠2=∠ABF,∠1+∠CBF=180°.
∵五边形ABCDE是正五边形,
∴∠ABC==108°.
∴∠1-∠2=180°-∠CBF-∠ABF=180°-(∠CBF+∠ABF)=180°-∠ABC=72°.
20.
解:(1)∠B=108°
(2)∵∠BCA=∠BAC,∠B=108°,
∴∠BCA==36°,∴∠ACD=72°,
∵∠D=∠B=108°,∴∠ACD+∠D=180°,
∴AC∥DE
21.
解:(1)甲对,乙不对.
∵θ=360°,∴(n-2)×180°=360°,
解得n=4,
∵θ=630°,∴(n-2)×180°=630°,
解得n=,
∵n为整数,∴θ不能取630°
(2)根据题意得(n-2)×180+360=(n+x-2)×180,
解得x=2
22.
解:∵BE∥AD,∠D=80°,
∠A=140°,∴∠BEC=∠D=80°,
∠ABE=180°-∠A=180°-140°=40°.
又∵BE平分∠ABC,∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
23.
解:(1)∵所经过的路线正好构成一个外角是15°的正多边形,
∴360÷15=24,24×5=120(m).
答:小明一共走了120米.
(2)
(24-2)×180°=3
960°.
答:这个多边形的内角和是3
960°.
24.
解:∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°.
∵∠ABC和∠BCD的平分线交于点E,
∴∠EBC=∠ABC,∠BCE=∠BCD.
∴∠E=180°-∠EBC-∠BCE=180°-(∠ABC+∠BCD)=180°-×140°=110°.
25.
解:(1)设∠1的邻补角为∠5,∠2的邻补角为∠6.
∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
