人教版七年级上册数学 1.2.4 绝对值课后作业(Word版含答案)
文档属性
| 名称 | 人教版七年级上册数学 1.2.4 绝对值课后作业(Word版含答案) |
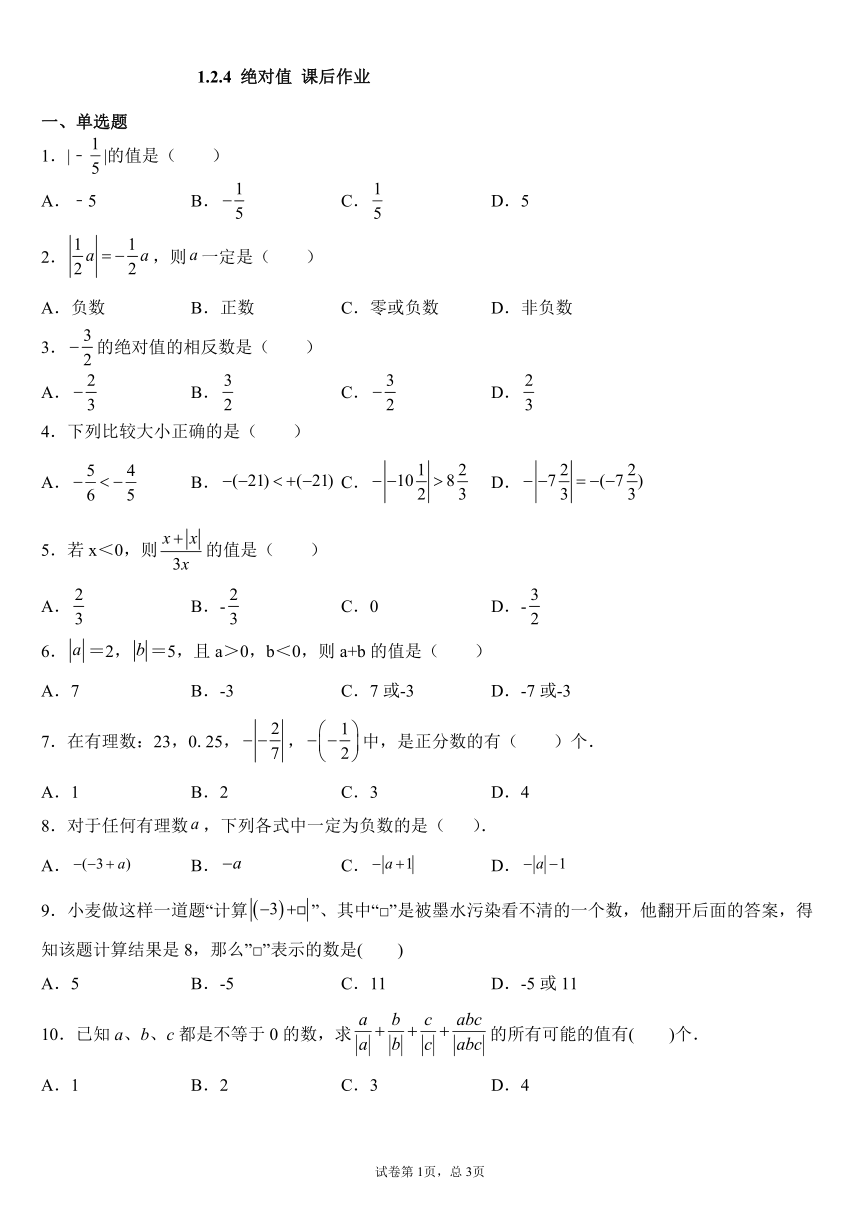
|
|
| 格式 | zip | ||
| 文件大小 | 116.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 00:00:00 | ||
图片预览
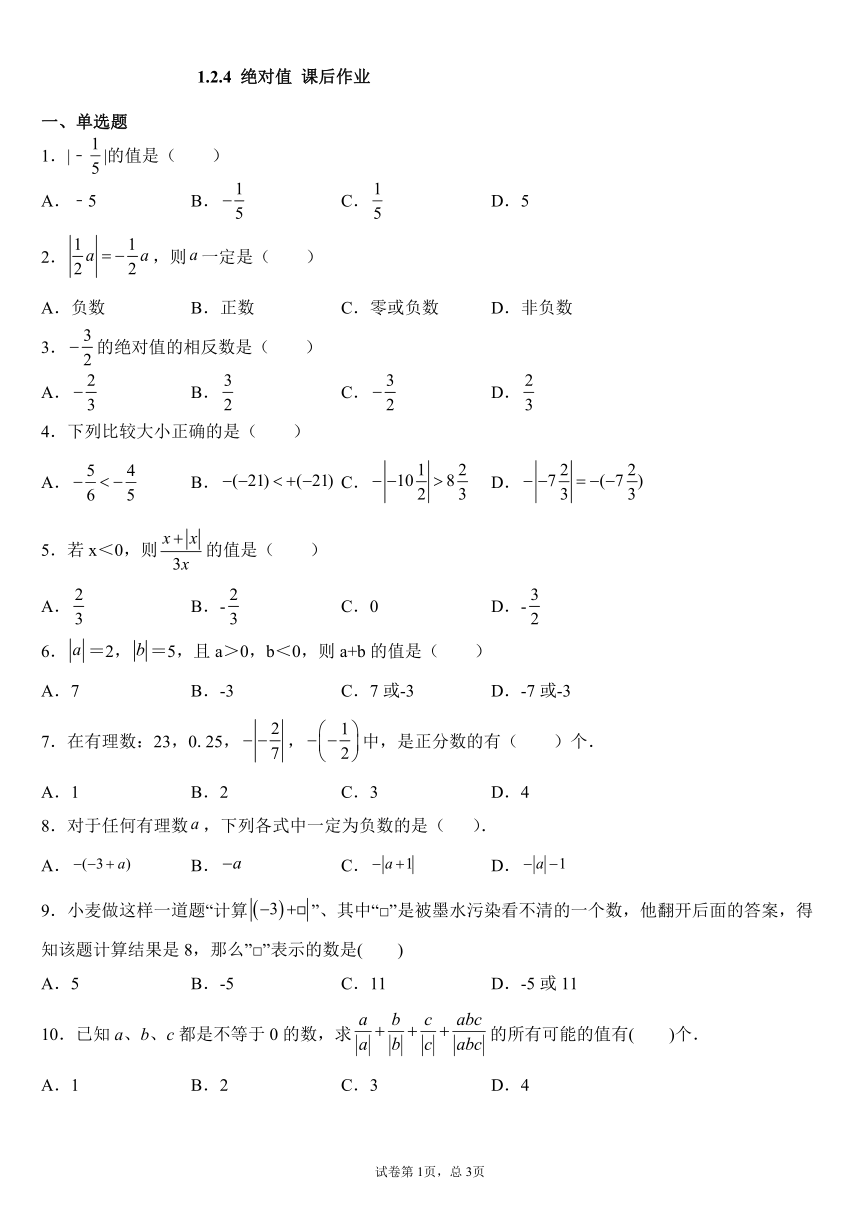


文档简介
1.2.4
绝对值
课后作业
一、单选题
1.|﹣|的值是(
)
A.﹣5
B.
C.
D.5
2.,则一定是(
)
A.负数
B.正数
C.零或负数
D.非负数
3.的绝对值的相反数是(
)
A.
B.
C.
D.
4.下列比较大小正确的是(
)
A.
B.
C.
D.
5.若x<0,则的值是(
)
A.
B.-
C.0
D.-
6.=2,=5,且a>0,b<0,则a+b的值是(
)
A.7
B.-3
C.7或-3
D.-7或-3
7.在有理数:23,0.25,,中,是正分数的有(
)个.
A.1
B.2
C.3
D.4
8.对于任何有理数,下列各式中一定为负数的是(
).
A.
B.
C.
D.
9.小麦做这样一道题“计算”、其中“□”是被墨水污染看不清的一个数,他翻开后面的答案,得知该题计算结果是8,那么”□”表示的数是(
)
A.5
B.-5
C.11
D.-5或11
10.已知a、b、c都是不等于0的数,求的所有可能的值有( )个.
A.1
B.2
C.3
D.4
二、填空题
11.计算:_________.
12.已知,则_________
13.已知取最小值,则____________。
14.同学们都知道:|5﹣(2)|表示
5
与﹣2
之差的绝对值,实际上也可
理解为
5
与﹣2
两数在数轴上所对应的两点之间的距离,同理,|x+2|+|x﹣3|
可以表示数轴上有理数
x
所对应的点到﹣2
和
3
所对应的点的距离之和,则使得|x+3|+|x﹣2|取得最小值的正整数
x
为
_______
.
15.已知a,b两数在数轴上的位置如图所示,则化简代数式的结果是____.
16.若,则的值是________.
三、解答题
17.有理数、、在数轴上的位置如图:
(1)判断正负,用“>”或“<”填空:
, , .
(2)化简:.
18.已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a
6
-6
-6
-6
2
-1.5
b
4
0
4
-4
-10
-1.5
A、B两点的距离
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,取得的值最小?
最小值是多少?
19.阅读下列材料并解决有关问题:
我们知道,|m|=
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令
m+1=0
和
m﹣2=0,分别求得
m=﹣1,m=2(称﹣1,2
分别为|m+1|与|m﹣2|的零点值).在实数范围内,
零点值
m=﹣1
和
m=2
可将全体实数分成不重复且不遗漏的如下
3
种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2|
可分以下
3
种情况:
(1)当
m<﹣1
时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2
时,原式=m+1﹣(m﹣2)=3;
(3)当
m≥2
时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
20.(1)设a、b为有理数,比较|a+b|与|a|+|b|(a、b为有理数)的大小关系,并用文字语言叙述此关系;
(2)根据(1)中的结论,当|x|+2018=|x-2018|时,则x的取值范围为
.
(3)已知a、b、c、d是有理数,|a-b|≤6,|c-d|≤16,|a-b-c+d|=22,求|b-a|-|d-c|的值
试卷第2页,总3页
试卷第1页,总3页
答案
1.C
2.C
3.C
4.A
5.C
6.B
7.B
8.D
9.D
10.C
11.2
12.2或-3
13.4
14.1或2.
15.3
16.-4
17.解(1)由数轴可得:c-b<0,a+b<0,a-c>0;
(2)
.
18.解(1)由题意,得
A、B两点间的距离依次为:2,6,10,2,12,0;
(2)由题意,得
(3)到两定点距离之和等于两定点之间的距离的点的集合是两定点之间的连线
故p点一定在5和-5之间
这样的整数点有1,2,3,4,5,-5,-4,-3,-2,-1,0
故它们的和为0;
(4)由题意,得
表示x到-1的距离,同理表示x到2的距离,
∴点C在-1和2之间时,取得最小值,最小值为3.
19.解(1)令
x﹣5=0,x﹣4=0,
解得:x=5
和
x=4,
故|x﹣5|和|x﹣4|的零点值分别为
5
和
4;
(2)当
x<4
时,原式=5﹣x+4﹣x=9﹣2x;
当
4≤x<5
时,原式=5﹣x+x﹣4=1;
当
x≥5
时,原式=x﹣5+x﹣4=2x﹣9.
综上讨论,原式=.
(3)当
x<4
时,原式=9﹣2x>1;
当
4≤x<5
时,原式=1;
当
x≥5
时,原式=2x﹣9>1.
20.解:(1)当a、b同号时,|a+b|=|a|+|b|,
当a、b异号时,|a+b|<|a|+|b|,
当a、b至少有一个为0时,|a+b|=|a|+|b|,
综上,|a|+|b|≥|a+b|(当
a、b同号或者至少有一个等于0时取等号),
文字表述:两数绝对值的和大于等于这两个数和的绝对值;
(2)∵
|-2018|=2018
∴
|x|+2018=|x|+|-2018|=|x-2018|,
∴x≤0,
即:当|x|+2018=|x-2018|时,x≤0,
故答案为:x≤0;
(3)∵
|a-b|≤6,|c-d|≤16,|a-b-c+d|=22,
∴
|a-b-c+d|=|(a-b)-(c-d)|=22,
∴
(a-b)与(c-d)
异号,且|a-b|=6,|c-d|=16,
∴
|b-a|-|d-c|=6-16=-10.
答案第2页,总2页
绝对值
课后作业
一、单选题
1.|﹣|的值是(
)
A.﹣5
B.
C.
D.5
2.,则一定是(
)
A.负数
B.正数
C.零或负数
D.非负数
3.的绝对值的相反数是(
)
A.
B.
C.
D.
4.下列比较大小正确的是(
)
A.
B.
C.
D.
5.若x<0,则的值是(
)
A.
B.-
C.0
D.-
6.=2,=5,且a>0,b<0,则a+b的值是(
)
A.7
B.-3
C.7或-3
D.-7或-3
7.在有理数:23,0.25,,中,是正分数的有(
)个.
A.1
B.2
C.3
D.4
8.对于任何有理数,下列各式中一定为负数的是(
).
A.
B.
C.
D.
9.小麦做这样一道题“计算”、其中“□”是被墨水污染看不清的一个数,他翻开后面的答案,得知该题计算结果是8,那么”□”表示的数是(
)
A.5
B.-5
C.11
D.-5或11
10.已知a、b、c都是不等于0的数,求的所有可能的值有( )个.
A.1
B.2
C.3
D.4
二、填空题
11.计算:_________.
12.已知,则_________
13.已知取最小值,则____________。
14.同学们都知道:|5﹣(2)|表示
5
与﹣2
之差的绝对值,实际上也可
理解为
5
与﹣2
两数在数轴上所对应的两点之间的距离,同理,|x+2|+|x﹣3|
可以表示数轴上有理数
x
所对应的点到﹣2
和
3
所对应的点的距离之和,则使得|x+3|+|x﹣2|取得最小值的正整数
x
为
_______
.
15.已知a,b两数在数轴上的位置如图所示,则化简代数式的结果是____.
16.若,则的值是________.
三、解答题
17.有理数、、在数轴上的位置如图:
(1)判断正负,用“>”或“<”填空:
, , .
(2)化简:.
18.已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a
6
-6
-6
-6
2
-1.5
b
4
0
4
-4
-10
-1.5
A、B两点的距离
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,取得的值最小?
最小值是多少?
19.阅读下列材料并解决有关问题:
我们知道,|m|=
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令
m+1=0
和
m﹣2=0,分别求得
m=﹣1,m=2(称﹣1,2
分别为|m+1|与|m﹣2|的零点值).在实数范围内,
零点值
m=﹣1
和
m=2
可将全体实数分成不重复且不遗漏的如下
3
种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2|
可分以下
3
种情况:
(1)当
m<﹣1
时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2
时,原式=m+1﹣(m﹣2)=3;
(3)当
m≥2
时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
20.(1)设a、b为有理数,比较|a+b|与|a|+|b|(a、b为有理数)的大小关系,并用文字语言叙述此关系;
(2)根据(1)中的结论,当|x|+2018=|x-2018|时,则x的取值范围为
.
(3)已知a、b、c、d是有理数,|a-b|≤6,|c-d|≤16,|a-b-c+d|=22,求|b-a|-|d-c|的值
试卷第2页,总3页
试卷第1页,总3页
答案
1.C
2.C
3.C
4.A
5.C
6.B
7.B
8.D
9.D
10.C
11.2
12.2或-3
13.4
14.1或2.
15.3
16.-4
17.解(1)由数轴可得:c-b<0,a+b<0,a-c>0;
(2)
.
18.解(1)由题意,得
A、B两点间的距离依次为:2,6,10,2,12,0;
(2)由题意,得
(3)到两定点距离之和等于两定点之间的距离的点的集合是两定点之间的连线
故p点一定在5和-5之间
这样的整数点有1,2,3,4,5,-5,-4,-3,-2,-1,0
故它们的和为0;
(4)由题意,得
表示x到-1的距离,同理表示x到2的距离,
∴点C在-1和2之间时,取得最小值,最小值为3.
19.解(1)令
x﹣5=0,x﹣4=0,
解得:x=5
和
x=4,
故|x﹣5|和|x﹣4|的零点值分别为
5
和
4;
(2)当
x<4
时,原式=5﹣x+4﹣x=9﹣2x;
当
4≤x<5
时,原式=5﹣x+x﹣4=1;
当
x≥5
时,原式=x﹣5+x﹣4=2x﹣9.
综上讨论,原式=.
(3)当
x<4
时,原式=9﹣2x>1;
当
4≤x<5
时,原式=1;
当
x≥5
时,原式=2x﹣9>1.
20.解:(1)当a、b同号时,|a+b|=|a|+|b|,
当a、b异号时,|a+b|<|a|+|b|,
当a、b至少有一个为0时,|a+b|=|a|+|b|,
综上,|a|+|b|≥|a+b|(当
a、b同号或者至少有一个等于0时取等号),
文字表述:两数绝对值的和大于等于这两个数和的绝对值;
(2)∵
|-2018|=2018
∴
|x|+2018=|x|+|-2018|=|x-2018|,
∴x≤0,
即:当|x|+2018=|x-2018|时,x≤0,
故答案为:x≤0;
(3)∵
|a-b|≤6,|c-d|≤16,|a-b-c+d|=22,
∴
|a-b-c+d|=|(a-b)-(c-d)|=22,
∴
(a-b)与(c-d)
异号,且|a-b|=6,|c-d|=16,
∴
|b-a|-|d-c|=6-16=-10.
答案第2页,总2页
