人教版初中数学 七年级上册1.2.2 数轴 课件(共34张PPt)
文档属性
| 名称 | 人教版初中数学 七年级上册1.2.2 数轴 课件(共34张PPt) |  | |
| 格式 | zip | ||
| 文件大小 | 956.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 15:52:19 | ||
图片预览









文档简介
(共34张PPT)
名言欣赏:
数学是一种精神,一种理性的精神。正是这种精神,激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度。
1、什么是有理数?
2、有理数的分类?
3、整数中除了正整数和负整数,还有什么数?
温故知新
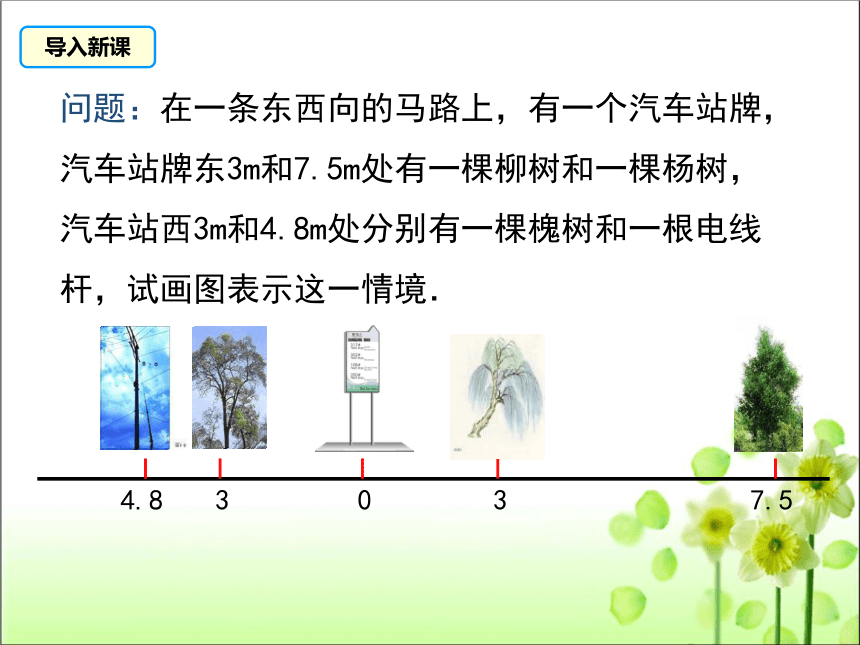
问题:在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
导入新课
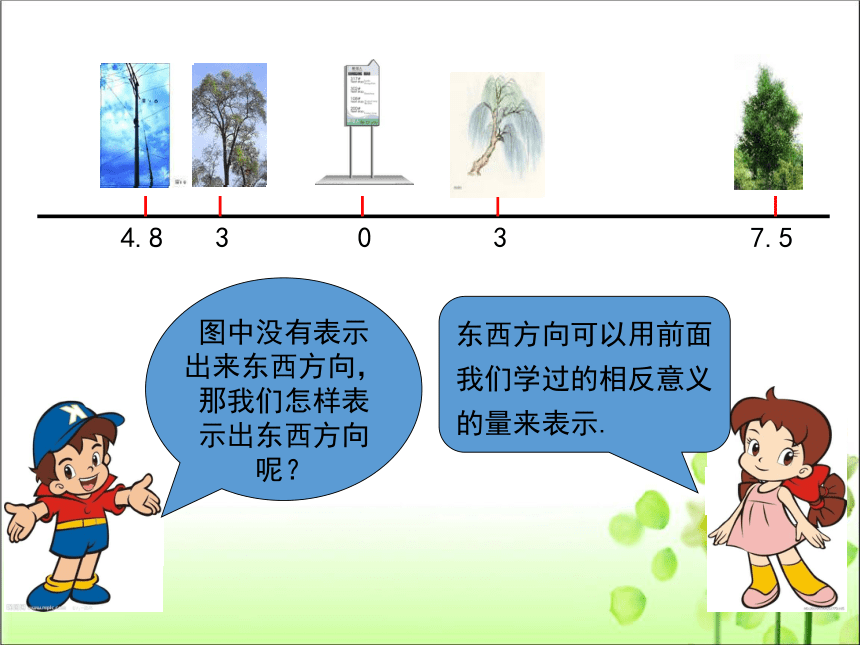
图中没有表示出来东西方向,那我们怎样表示出东西方向呢?
东西方向可以用前面我们学过的相反意义的量来表示.
0
3
7.5
3
4.8
思考:怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
为了使表达更清楚,我们规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
-4.8
-3
0
1
3
7.5
我们把正数、0和负数用一条直线上的点表示出来.
1.2
有理数
第一章
有理数
1.2.2
数轴
目标导航
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.(重点)
2.会正确的画出数轴,利用数轴上的点表示有理数.(难点)
0
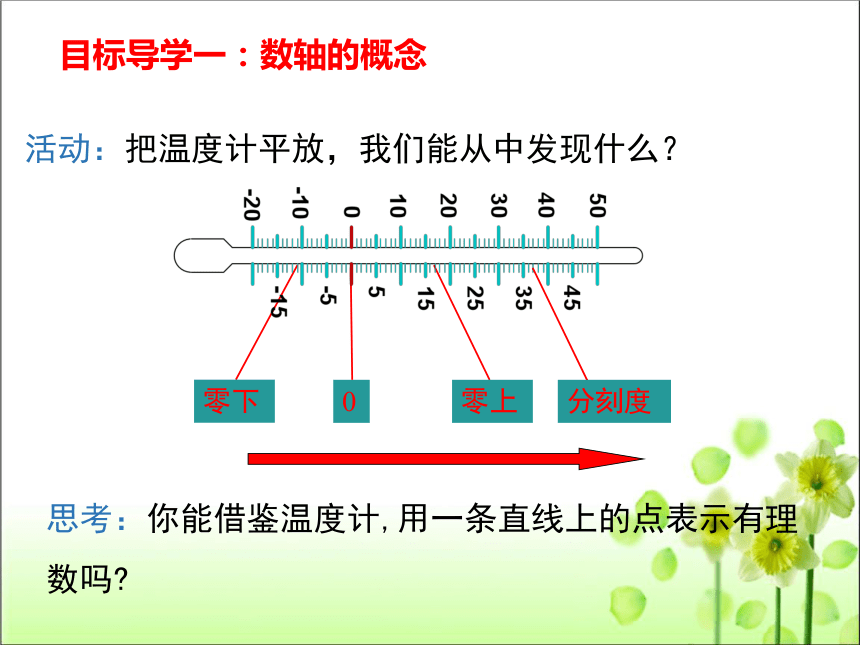
活动:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗?
目标导学一:数轴的概念
画一条水平直线,在直线上取一点表示0,并把这个点叫作原点,选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到下面的数轴.
类比归纳
数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.
(1)在直线上任取一个点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…
0
正方向
1
2
3
-1
-2
-3
归纳:规定了原点、正方向、单位长度的直线叫数轴。
数轴的三要素:原点、正方向、单位长度。(三者缺一不可)
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从
原点向左)则为负方向.
3.选择适当的长度为单位长度.
?
0
0
1
2
3
-1
-2
-3
?
?
画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.
1、画数轴
0
1
2
3
-1
-2
-3
4
-4
3.5
2、丰富数轴的内涵:分数或小数也可以用数轴上的点来表示,例如从原点向右3.5个单位长度的点表示小数3.5,从原点向左
个单位长度的点表示分数
2
3
-
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、正方向、单位长度一个也不能少.
试一试:判断下面所画数轴是否正确,并说明理由
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻
度均匀.
画数轴注意事项:
归纳总结
例1:说出数轴上点A,B,C,D,E所表示的数:
解:
A表示0;
B表示-2;
C表示1;
D表示2.5;
E表示-3
练习
写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
2、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
不能
这个点存在
目标导学二:在数轴上表示有理数
例2
在所给数轴上画出表示下列各数的点.
1,-5,-2.5,
,0
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方,
以便观看.
4
典例精析
练习
画出数轴并表示下列有理数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
分数和小数在数轴上能表示吗?
请试着在数轴上表示出6.5,
.
0
1
2
3
-1
-2
-3
-4
-5
-6
4
5
6
6.5
一般地,设a是一个正数,则数轴上表示数a的点在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
观察数轴上有理数排列的大小规律:
右
a
左
a
0
1
2
3
-1
-2
-3
归纳
0
1
2
3
-1
-2
-3
数轴上两个点所表示数,右边的总比左边的大。
正数大于0,负数小于0,正数大于负数。
越
来
越
大
发现规律:
例3
从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是
,再向右移动5个单位长度到达点C,则点C表示的数是
.
0
-3
-2
-1
1
2
3
C
.
.
解析:如图,
左移2个
右移5个
.
B
-3
2
在数轴上P点表示2,现在将P点向右移动两个单位长度后再向左移动5个单位长度,这时P点表示的数是_______.
变式练习
-1
目标检测
C
1、下列说法中正确的是(
)
A.
在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C.
一个有理数总可以在数轴上找到一个表示它的点
D.
所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
A
1
2、下列图形中哪些是数轴,哪些不是,为什么?
B
1
0
2
-1
D
0
-2
1
2
E
1
2
1
2
-1
-1
-2
-2
0
x
y
C
0
-1
2
3
-1
3、练习:在数轴上表示下列有理数:1.5,-2,2,-2.5,
,
,0
.
0
2
-2
1.5
-2.5
4、点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为
(
)
A.2
B.-6
C.2或-6
D.不同于以上
C
5、思考:你觉得数轴上的点表示数的大小与点的位置有什么关系?
数轴上的点与实数一一对应;原点的左边的位置所示的数小于0,原点右边的位置所示的数大于0,原点处所示的数等于0;数轴右边的数大于在左边的。
概念
数轴的三要素
数与形的关系
一般地,在数学中人们用画图把数“直观化”.用一条直线上的点表示数,这条直线叫做数轴;
数轴
原点、正方向、单位长度;
对应的关系;
数学思想
数形结合的思想.
有理数
数轴上的点
(数)
(形)
转
化
课堂小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
1.整理本节知识
2.完成同步练习题
名言欣赏:
数学是一种精神,一种理性的精神。正是这种精神,激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度。
1、什么是有理数?
2、有理数的分类?
3、整数中除了正整数和负整数,还有什么数?
温故知新
问题:在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
导入新课
图中没有表示出来东西方向,那我们怎样表示出东西方向呢?
东西方向可以用前面我们学过的相反意义的量来表示.
0
3
7.5
3
4.8
思考:怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
为了使表达更清楚,我们规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
-4.8
-3
0
1
3
7.5
我们把正数、0和负数用一条直线上的点表示出来.
1.2
有理数
第一章
有理数
1.2.2
数轴
目标导航
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.(重点)
2.会正确的画出数轴,利用数轴上的点表示有理数.(难点)
0
活动:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗?
目标导学一:数轴的概念
画一条水平直线,在直线上取一点表示0,并把这个点叫作原点,选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到下面的数轴.
类比归纳
数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.
(1)在直线上任取一个点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…
0
正方向
1
2
3
-1
-2
-3
归纳:规定了原点、正方向、单位长度的直线叫数轴。
数轴的三要素:原点、正方向、单位长度。(三者缺一不可)
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从
原点向左)则为负方向.
3.选择适当的长度为单位长度.
?
0
0
1
2
3
-1
-2
-3
?
?
画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.
1、画数轴
0
1
2
3
-1
-2
-3
4
-4
3.5
2、丰富数轴的内涵:分数或小数也可以用数轴上的点来表示,例如从原点向右3.5个单位长度的点表示小数3.5,从原点向左
个单位长度的点表示分数
2
3
-
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、正方向、单位长度一个也不能少.
试一试:判断下面所画数轴是否正确,并说明理由
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻
度均匀.
画数轴注意事项:
归纳总结
例1:说出数轴上点A,B,C,D,E所表示的数:
解:
A表示0;
B表示-2;
C表示1;
D表示2.5;
E表示-3
练习
写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
2、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
不能
这个点存在
目标导学二:在数轴上表示有理数
例2
在所给数轴上画出表示下列各数的点.
1,-5,-2.5,
,0
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方,
以便观看.
4
典例精析
练习
画出数轴并表示下列有理数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
分数和小数在数轴上能表示吗?
请试着在数轴上表示出6.5,
.
0
1
2
3
-1
-2
-3
-4
-5
-6
4
5
6
6.5
一般地,设a是一个正数,则数轴上表示数a的点在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
观察数轴上有理数排列的大小规律:
右
a
左
a
0
1
2
3
-1
-2
-3
归纳
0
1
2
3
-1
-2
-3
数轴上两个点所表示数,右边的总比左边的大。
正数大于0,负数小于0,正数大于负数。
越
来
越
大
发现规律:
例3
从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是
,再向右移动5个单位长度到达点C,则点C表示的数是
.
0
-3
-2
-1
1
2
3
C
.
.
解析:如图,
左移2个
右移5个
.
B
-3
2
在数轴上P点表示2,现在将P点向右移动两个单位长度后再向左移动5个单位长度,这时P点表示的数是_______.
变式练习
-1
目标检测
C
1、下列说法中正确的是(
)
A.
在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C.
一个有理数总可以在数轴上找到一个表示它的点
D.
所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
A
1
2、下列图形中哪些是数轴,哪些不是,为什么?
B
1
0
2
-1
D
0
-2
1
2
E
1
2
1
2
-1
-1
-2
-2
0
x
y
C
0
-1
2
3
-1
3、练习:在数轴上表示下列有理数:1.5,-2,2,-2.5,
,
,0
.
0
2
-2
1.5
-2.5
4、点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为
(
)
A.2
B.-6
C.2或-6
D.不同于以上
C
5、思考:你觉得数轴上的点表示数的大小与点的位置有什么关系?
数轴上的点与实数一一对应;原点的左边的位置所示的数小于0,原点右边的位置所示的数大于0,原点处所示的数等于0;数轴右边的数大于在左边的。
概念
数轴的三要素
数与形的关系
一般地,在数学中人们用画图把数“直观化”.用一条直线上的点表示数,这条直线叫做数轴;
数轴
原点、正方向、单位长度;
对应的关系;
数学思想
数形结合的思想.
有理数
数轴上的点
(数)
(形)
转
化
课堂小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
1.整理本节知识
2.完成同步练习题
