3.1直线的倾斜角与斜率 同步练习(含解析)
文档属性
| 名称 | 3.1直线的倾斜角与斜率 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 08:41:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教新课标A版
必修二
3.1直线的倾斜角与斜率
一、单选题
1.直线经过点(0,2)和点(3,0),则它的斜率为(???
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.若直线经过
A(0,1),B(,4)两点,则直线AB的倾斜角为(???
)
A.?30°??????????????????????????????????????B.?45°??????????????????????????????????????C.?60°??????????????????????????????????????D.?120°
3.直线
的斜率为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
4.直线
的倾斜角为(???
)
A.?30°?????????????????????????????????????B.?60°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
5.过点
且斜率不存在的直线方程为(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.直线l1的倾斜角
,直线l1⊥l2
,
则直线l2的斜率为(???
)
A.?-
?????????????????????????????????????B.??????????????????????????????????????C.?-
?????????????????????????????????????D.?
7.已知经过两点
和
的直线的斜率大于1,则
的取值范围是(???
)
A.?(5,8)???????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
8.如图所示,直线
的斜率分别为
,则(??
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
9.下列各对直线不互相垂直的是(
??)
A.?l1的倾斜角为120°,l2过点P(1,0),Q(4,
)??????????
B.?l1的斜率为-
,l2过点P(1,1),Q
C.?l1的倾斜角为30°,l2过点P(3,
),Q(4,2
)??????????
D.?l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
10.已知点A(1,3),B(-2,-1),若直线l:y=k(x-2)+1与线段AB有公共点,则k的取值范围是(???
)
A.???????????????????????B.???????????????????????C.?或
??????????????????????D.?
11.若直线
经过点
,且在
轴上的截距的取值范围是
,则其斜率的取值范围是(??
)
A.??????????????????B.?或
?????????????????C.?或
?????????????????D.?
12.已知两点
,直线
与线段
相交,则直线
的斜率取值范围是(
??)
A.??????????????B.??????????????C.??????????????D.?
二、多选题
13.在下列四个命题中,错误的有(???
)
A.?坐标平面内的任何一条直线均有倾斜角和斜率
B.?直线的倾斜角的取值范围是
C.?若一条直线的斜率为
,则此直线的倾斜角为
D.?若一条直线的倾斜角为
,则此直线的斜率为
三、填空题
14.已知
、
,
,若
三点共线,则
=________
15.若直线
和直线
的倾斜角分别为
和
则
与
的夹角为________.
16.直线l过点P(1,0),且与以A(2,1),B(0,
)为端点的线段有公共点,则直线l斜率的取值范围是________.
17.直线l:ax+(a+1)y+2=0的倾斜角大于45°,则a的取值范围是________.
四、解答题
18.经过下列两点的直线的斜率是否存在?如果存在,求其斜率,并确定直线的倾斜角α.
(1)A(2,3),B(4,5);
(2)C(-2,3),D(2,-1);
(3)P(-3,1),Q(-3,10).
19.已知直线
经过两点
,问:当
取何值时:
(1)与
轴平行?
(2)与
轴平行?
(3)的斜率为
?
20.直线l1经过点A(m,1),B(-3,4),直线l2经过点C(1,m),D(-1,m+1),当l1∥l2或l1⊥l2时,分别求实数m的值.
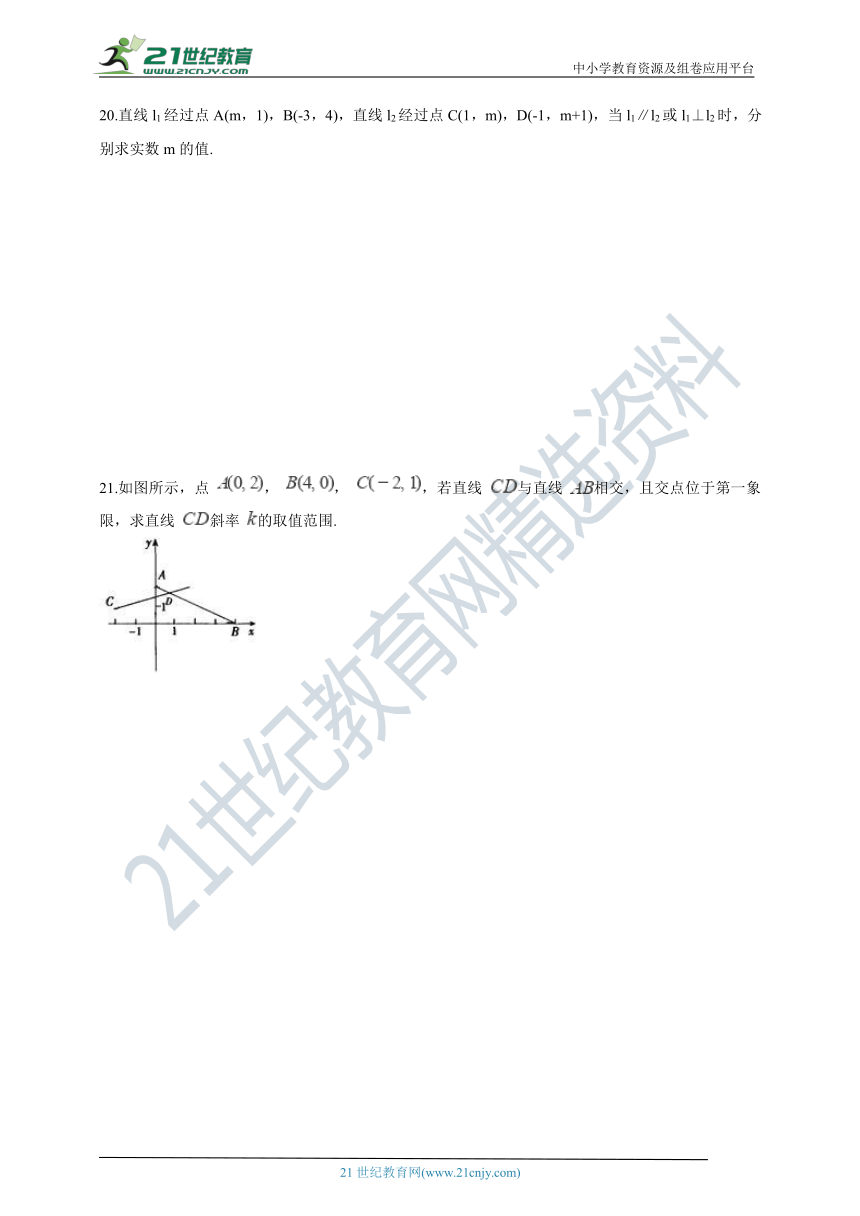
21.如图所示,点
,
,
,若直线
与直线
相交,且交点位于第一象限,求直线
斜率
的取值范围.
22.已知
的点
,
,
.
(1)判断
的形状;
(2)设D,E分别为AB,AC的中点,求直线DE的斜率;
23.已知A(-1,1),B(1,1),C(2,
+1),
(1)求直线AB和AC的斜率.
(2)若点D在线段AB(包括端点)上移动时,求直线CD的斜率的变化范围.
答案解析部分
一、单选题
1.答案:
C
解:由题意,直线经过点
和点
,
则直线
的斜率是
,
故答案为:C.
【分析】直接利用直线的斜率公式,即可求解经过两点的直线的斜率,得到答案.
2.答案:
C
解:设直线AB的倾斜角为α,直线经过
A(0,1),B(,4)
两点,
所以,即tanα=,
又因为0°≤α
<180°
,所以
α=60°
.
故答案为:C
【分析】本题主要考查了直线的倾斜角、直线的斜率、斜率的计算公式,解决问题的关键是根据直线倾斜角与斜率的关系进行计算即可.
3.答案:
C
解:
可化为
,则
故答案为:C
【分析】
可化为
,即可得出斜率.
4.答案:
C
解:由直线方程可知直线的斜率
,
故答案为:C.
【分析】利用直线的倾斜角和直线的斜率之间的关系式,再利用直线的倾斜角的取值范围,从而求出直线
的倾斜角。
5.答案:
B
解:根据题意,过点
且斜率不存在的直线方程为
故答案为:B.
【分析】根据题意,结合直线的方程的形式即可得答案.
6.答案:
C
解:如图:直线L1的倾斜角α1=30°,直线L1⊥L2
,
则L2的倾斜角等于30°+90°=120°,
∴L2的斜率为
tan120°=﹣tan60°
,
故答案为:C.
【分析】由题意可得L2的倾斜角等于30°+90°=120°,从而得到L2的斜率为
tan120°,运算求得结果.
7.答案:
D
解:由题意得
,即
,解得
.
故答案为:D.
【分析】表示过两点的斜率,解不等式即可求出实数m的取值范围.
8.答案:
B
解:由图可知,直线
的倾斜角为锐角,所以
,
而直线
与
的倾斜角均为钝角,且
的倾斜角小于
的倾斜角,
故
.所以
.
故答案为:B.
【分析】设直线
所对应的倾斜角为
,
由图可知
,由直线的倾斜角与斜率的关系可得
,得解.
9.答案:
C
解:A.l1的倾斜角为120°,l2过点P(1,0),Q(4,
),kPQ=
,
故两直线垂直,故A不符合题意;
B.l2过点P(1,1),Q
,kPQ=
,故两条直线垂直两条,故B不符合题意;
C,
kPQ=
,所以l1不与l2垂直,故C符合题意;
D,l1过点M(1,0),N(4,-5),
?,l2过点P(-6,0),Q(-1,3),kPQ=
,
故两条直线垂直,故D不符合题意.
故答案为:C.
【分析】两条直线互相垂直,那么这两条直线的斜率积为-1.
10.答案:
D
解:因为直线l:y=k(x-2)+1恒过定点
,
如图所示:
若直线l:y=k(x-2)+1与线段AB有公共点,
则
,
又
,
,
所以
.
故答案为:D.
【分析】先由条件画出图象,再求出直线l与线段
有交点的条件,进而可求出答案.
11.答案:
C
解:因为直线
过点
,在x轴上的截距取值范围是
,
所以直线端点的斜率分别为:
?,如图:
所以
或
.
故答案为:C.
【分析】利用两点求斜率公式结合直线经过点
,且在
轴上的截距的取值范围是
所做的图象,从而求出直线斜率的取值范围。
12.答案:
A
解:直线
过定点
,
,
,
直线
与线段
相交,
则直线
的斜率取值范围是
.
故答案为:
.
【分析】求出直线所过定点
,画出图形,再求出
,
的斜率,数形结合得答案.
二、多选题
13.答案:
A,C,D
解:对于A,当直线与
轴垂直时,直线的倾斜角为
,斜率不存在,A不符合题意
对于B,直线倾斜角的取值范围是
,B符合题意
对于C,一条直线的斜率为
,此直线的倾斜角不一定为
,
如
的斜率为
,它的倾斜角为
,C不符合题意,
对于D,一条直线的倾斜角为
时,它的斜率为
或不存在,D不符合题意
故答案为:ACD
【分析】A中,直线与
轴垂直时,直线的倾斜角为
,斜率不存在
B中,直线倾斜角的取值范围是
C中,直线的斜率为
时,它的倾斜角不一定为
D中,直线的倾斜角为
时,它的斜率为
或不存在
三、填空题
14.答案:
2
解:∵,
,
三点共线,
∴,
即,
解得:,
故答案为:2
【分析】由三点共线,得出任意两点的斜率相等,列出方程,求出的值。
15.答案:
解:直线l1和l2的倾斜角分别为32°和152°,
所以直线l1和l2的夹角为180°﹣(152°﹣32°)=60°.
故答案为:60°.
【分析】直接利用角的运算的应用求出结果.
16.答案:
(-∞,-
]∪[1,+∞)
解:如图示:
当直线l过点
时设直线l斜率为
,
则
,
当直线l过点
时设直线l斜率为
,
则
,
要使直线l
与线段
有公共点,
?则直线l斜率的取值范围是(-∞,-
]∪[1,+∞),
故答案为:(-∞,-
]∪[1,+∞).
【分析】作出函数的图像,求出端点处的斜率,从而求出斜率的范围即可.
17.答案:
解:当a=-1时,直线l的倾斜角为90°,符合要求;
当a≠-1时,直线l的斜率为
,
只要
>1或者
<0即可,
解得-1或者a<-1或者a>0.
综上可知,实数a的取值范围是(-∞,-
)∪(0,+∞).
【分析】由已知利用倾斜角与直线斜率的关系列式,即可求出实数a的取值范围.
四、解答题
18.答案:
(1)解:
存在.直线AB的斜率kAB=
=1,即tanα=1,
又0°≤α<180°,所以倾斜角α=45°
(2)解:
存在.直线CD的斜率kCD=
=-1,即tanα=-1,
又0°≤α<180°,所以倾斜角α=135°.
(3)解:
不存在.因为xP=xQ=-3,所以直线PQ的斜率不存在,倾斜角α=90°.
【分析】(1)利用斜率计算公式,代入数据,即可得出答案。(2)结合斜率计算公式,即可得出答案。(3)结合斜率计算公式,即可得出答案。
19.答案:
(1)解:当直线
与
轴平行时,直线
的斜率为0,此时
(2)解:当
与
轴平行时,直线
不存在斜率,此时
(3)解:当
的斜率为
时,有
,解得
.
故当
时,
与
轴平行;当
时,
与
轴平行;
当
,
的斜率为
【分析】由过两点的斜率公式表示出斜率,由各小题的条件得到关于m的方程,求解.
20.答案:解:当l1∥l2时,由于直线l2的斜率k2存在,
则直线l1的斜率k1也存在,则k1=k2
,
即
=
,解得m=3;
当l1⊥l2时,由于直线l2的斜率k2存在且不为0,
则直线l1的斜率k1也存在,则k1·k2=-1,
即
·
=-1,解得m=-
.
综上所述,当l1∥l2时,m的值为3;当l1⊥l2时,m的值为-
.
【分析】必须先判断两直线是否存在斜率不存在的情况,再依据两直线平行则两直线的斜率相等,两直线垂直,则两两直线的斜率积为-1进行解题.
21.答案:解:连接
,
,设直线
的倾斜角为
,直线
的倾斜角为
,
则直线
的倾斜角
满足:
,或
,
所以直线
的斜率
满足
,
或
,所以
.
【分析】由直线C
D与直线A
B相交,且交点位于第一象限,结合图形得到直线
BC和CD的倾斜角应满足的条件,转化为斜率满足的不等式,求k的范围.
22.答案:
(1)解:
,
,
,
,
,
.
设F为BC的中点,则
,
.
由于
,
,
是等腰直角三角形
(2)解:由于D,E分别为AB,AC的中点,
,即
.
故直线DE的斜率为
【分析】(1)根据A,B,C的坐标表示相应直线的斜率,根据两直线斜率之积为-1,两直线互相垂直,确定三角形的形状即可;
(2)根据三角形的中位线平行于第三边,结合平行线的斜率相等即可求出直线DE的斜率.
23.答案:
(1)解:由斜率公式得:
kAB=
=0,kAC=
=
,
所以直线AB的斜率为0,直线AC的斜率为
(2)解:如图所示:
由斜率公式可得kBC=
=
.
设直线CD的斜率为k,
结合图形可得当直线CD由CA的位置按逆时针方向旋转到CB的位置时,
直线CD与AB恒有交点,此时k由kCA增大到kCB
,
所以
即k的取值范围为
【分析】(1)根据题意结合已知条件利用直线斜率的坐标公式代入数值求出结果即可。(2)根据题意结合已知条件作出图像结合图形可得当直线CD由CA的位置按逆时针方向旋转到CB的位置时,直线CD与AB恒有交点进而得出k的取值范围。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教新课标A版
必修二
3.1直线的倾斜角与斜率
一、单选题
1.直线经过点(0,2)和点(3,0),则它的斜率为(???
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.若直线经过
A(0,1),B(,4)两点,则直线AB的倾斜角为(???
)
A.?30°??????????????????????????????????????B.?45°??????????????????????????????????????C.?60°??????????????????????????????????????D.?120°
3.直线
的斜率为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
4.直线
的倾斜角为(???
)
A.?30°?????????????????????????????????????B.?60°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
5.过点
且斜率不存在的直线方程为(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.直线l1的倾斜角
,直线l1⊥l2
,
则直线l2的斜率为(???
)
A.?-
?????????????????????????????????????B.??????????????????????????????????????C.?-
?????????????????????????????????????D.?
7.已知经过两点
和
的直线的斜率大于1,则
的取值范围是(???
)
A.?(5,8)???????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
8.如图所示,直线
的斜率分别为
,则(??
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
9.下列各对直线不互相垂直的是(
??)
A.?l1的倾斜角为120°,l2过点P(1,0),Q(4,
)??????????
B.?l1的斜率为-
,l2过点P(1,1),Q
C.?l1的倾斜角为30°,l2过点P(3,
),Q(4,2
)??????????
D.?l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
10.已知点A(1,3),B(-2,-1),若直线l:y=k(x-2)+1与线段AB有公共点,则k的取值范围是(???
)
A.???????????????????????B.???????????????????????C.?或
??????????????????????D.?
11.若直线
经过点
,且在
轴上的截距的取值范围是
,则其斜率的取值范围是(??
)
A.??????????????????B.?或
?????????????????C.?或
?????????????????D.?
12.已知两点
,直线
与线段
相交,则直线
的斜率取值范围是(
??)
A.??????????????B.??????????????C.??????????????D.?
二、多选题
13.在下列四个命题中,错误的有(???
)
A.?坐标平面内的任何一条直线均有倾斜角和斜率
B.?直线的倾斜角的取值范围是
C.?若一条直线的斜率为
,则此直线的倾斜角为
D.?若一条直线的倾斜角为
,则此直线的斜率为
三、填空题
14.已知
、
,
,若
三点共线,则
=________
15.若直线
和直线
的倾斜角分别为
和
则
与
的夹角为________.
16.直线l过点P(1,0),且与以A(2,1),B(0,
)为端点的线段有公共点,则直线l斜率的取值范围是________.
17.直线l:ax+(a+1)y+2=0的倾斜角大于45°,则a的取值范围是________.
四、解答题
18.经过下列两点的直线的斜率是否存在?如果存在,求其斜率,并确定直线的倾斜角α.
(1)A(2,3),B(4,5);
(2)C(-2,3),D(2,-1);
(3)P(-3,1),Q(-3,10).
19.已知直线
经过两点
,问:当
取何值时:
(1)与
轴平行?
(2)与
轴平行?
(3)的斜率为
?
20.直线l1经过点A(m,1),B(-3,4),直线l2经过点C(1,m),D(-1,m+1),当l1∥l2或l1⊥l2时,分别求实数m的值.
21.如图所示,点
,
,
,若直线
与直线
相交,且交点位于第一象限,求直线
斜率
的取值范围.
22.已知
的点
,
,
.
(1)判断
的形状;
(2)设D,E分别为AB,AC的中点,求直线DE的斜率;
23.已知A(-1,1),B(1,1),C(2,
+1),
(1)求直线AB和AC的斜率.
(2)若点D在线段AB(包括端点)上移动时,求直线CD的斜率的变化范围.
答案解析部分
一、单选题
1.答案:
C
解:由题意,直线经过点
和点
,
则直线
的斜率是
,
故答案为:C.
【分析】直接利用直线的斜率公式,即可求解经过两点的直线的斜率,得到答案.
2.答案:
C
解:设直线AB的倾斜角为α,直线经过
A(0,1),B(,4)
两点,
所以,即tanα=,
又因为0°≤α
<180°
,所以
α=60°
.
故答案为:C
【分析】本题主要考查了直线的倾斜角、直线的斜率、斜率的计算公式,解决问题的关键是根据直线倾斜角与斜率的关系进行计算即可.
3.答案:
C
解:
可化为
,则
故答案为:C
【分析】
可化为
,即可得出斜率.
4.答案:
C
解:由直线方程可知直线的斜率
,
故答案为:C.
【分析】利用直线的倾斜角和直线的斜率之间的关系式,再利用直线的倾斜角的取值范围,从而求出直线
的倾斜角。
5.答案:
B
解:根据题意,过点
且斜率不存在的直线方程为
故答案为:B.
【分析】根据题意,结合直线的方程的形式即可得答案.
6.答案:
C
解:如图:直线L1的倾斜角α1=30°,直线L1⊥L2
,
则L2的倾斜角等于30°+90°=120°,
∴L2的斜率为
tan120°=﹣tan60°
,
故答案为:C.
【分析】由题意可得L2的倾斜角等于30°+90°=120°,从而得到L2的斜率为
tan120°,运算求得结果.
7.答案:
D
解:由题意得
,即
,解得
.
故答案为:D.
【分析】表示过两点的斜率,解不等式即可求出实数m的取值范围.
8.答案:
B
解:由图可知,直线
的倾斜角为锐角,所以
,
而直线
与
的倾斜角均为钝角,且
的倾斜角小于
的倾斜角,
故
.所以
.
故答案为:B.
【分析】设直线
所对应的倾斜角为
,
由图可知
,由直线的倾斜角与斜率的关系可得
,得解.
9.答案:
C
解:A.l1的倾斜角为120°,l2过点P(1,0),Q(4,
),kPQ=
,
故两直线垂直,故A不符合题意;
B.l2过点P(1,1),Q
,kPQ=
,故两条直线垂直两条,故B不符合题意;
C,
kPQ=
,所以l1不与l2垂直,故C符合题意;
D,l1过点M(1,0),N(4,-5),
?,l2过点P(-6,0),Q(-1,3),kPQ=
,
故两条直线垂直,故D不符合题意.
故答案为:C.
【分析】两条直线互相垂直,那么这两条直线的斜率积为-1.
10.答案:
D
解:因为直线l:y=k(x-2)+1恒过定点
,
如图所示:
若直线l:y=k(x-2)+1与线段AB有公共点,
则
,
又
,
,
所以
.
故答案为:D.
【分析】先由条件画出图象,再求出直线l与线段
有交点的条件,进而可求出答案.
11.答案:
C
解:因为直线
过点
,在x轴上的截距取值范围是
,
所以直线端点的斜率分别为:
?,如图:
所以
或
.
故答案为:C.
【分析】利用两点求斜率公式结合直线经过点
,且在
轴上的截距的取值范围是
所做的图象,从而求出直线斜率的取值范围。
12.答案:
A
解:直线
过定点
,
,
,
直线
与线段
相交,
则直线
的斜率取值范围是
.
故答案为:
.
【分析】求出直线所过定点
,画出图形,再求出
,
的斜率,数形结合得答案.
二、多选题
13.答案:
A,C,D
解:对于A,当直线与
轴垂直时,直线的倾斜角为
,斜率不存在,A不符合题意
对于B,直线倾斜角的取值范围是
,B符合题意
对于C,一条直线的斜率为
,此直线的倾斜角不一定为
,
如
的斜率为
,它的倾斜角为
,C不符合题意,
对于D,一条直线的倾斜角为
时,它的斜率为
或不存在,D不符合题意
故答案为:ACD
【分析】A中,直线与
轴垂直时,直线的倾斜角为
,斜率不存在
B中,直线倾斜角的取值范围是
C中,直线的斜率为
时,它的倾斜角不一定为
D中,直线的倾斜角为
时,它的斜率为
或不存在
三、填空题
14.答案:
2
解:∵,
,
三点共线,
∴,
即,
解得:,
故答案为:2
【分析】由三点共线,得出任意两点的斜率相等,列出方程,求出的值。
15.答案:
解:直线l1和l2的倾斜角分别为32°和152°,
所以直线l1和l2的夹角为180°﹣(152°﹣32°)=60°.
故答案为:60°.
【分析】直接利用角的运算的应用求出结果.
16.答案:
(-∞,-
]∪[1,+∞)
解:如图示:
当直线l过点
时设直线l斜率为
,
则
,
当直线l过点
时设直线l斜率为
,
则
,
要使直线l
与线段
有公共点,
?则直线l斜率的取值范围是(-∞,-
]∪[1,+∞),
故答案为:(-∞,-
]∪[1,+∞).
【分析】作出函数的图像,求出端点处的斜率,从而求出斜率的范围即可.
17.答案:
解:当a=-1时,直线l的倾斜角为90°,符合要求;
当a≠-1时,直线l的斜率为
,
只要
>1或者
<0即可,
解得-1
综上可知,实数a的取值范围是(-∞,-
)∪(0,+∞).
【分析】由已知利用倾斜角与直线斜率的关系列式,即可求出实数a的取值范围.
四、解答题
18.答案:
(1)解:
存在.直线AB的斜率kAB=
=1,即tanα=1,
又0°≤α<180°,所以倾斜角α=45°
(2)解:
存在.直线CD的斜率kCD=
=-1,即tanα=-1,
又0°≤α<180°,所以倾斜角α=135°.
(3)解:
不存在.因为xP=xQ=-3,所以直线PQ的斜率不存在,倾斜角α=90°.
【分析】(1)利用斜率计算公式,代入数据,即可得出答案。(2)结合斜率计算公式,即可得出答案。(3)结合斜率计算公式,即可得出答案。
19.答案:
(1)解:当直线
与
轴平行时,直线
的斜率为0,此时
(2)解:当
与
轴平行时,直线
不存在斜率,此时
(3)解:当
的斜率为
时,有
,解得
.
故当
时,
与
轴平行;当
时,
与
轴平行;
当
,
的斜率为
【分析】由过两点的斜率公式表示出斜率,由各小题的条件得到关于m的方程,求解.
20.答案:解:当l1∥l2时,由于直线l2的斜率k2存在,
则直线l1的斜率k1也存在,则k1=k2
,
即
=
,解得m=3;
当l1⊥l2时,由于直线l2的斜率k2存在且不为0,
则直线l1的斜率k1也存在,则k1·k2=-1,
即
·
=-1,解得m=-
.
综上所述,当l1∥l2时,m的值为3;当l1⊥l2时,m的值为-
.
【分析】必须先判断两直线是否存在斜率不存在的情况,再依据两直线平行则两直线的斜率相等,两直线垂直,则两两直线的斜率积为-1进行解题.
21.答案:解:连接
,
,设直线
的倾斜角为
,直线
的倾斜角为
,
则直线
的倾斜角
满足:
,或
,
所以直线
的斜率
满足
,
或
,所以
.
【分析】由直线C
D与直线A
B相交,且交点位于第一象限,结合图形得到直线
BC和CD的倾斜角应满足的条件,转化为斜率满足的不等式,求k的范围.
22.答案:
(1)解:
,
,
,
,
,
.
设F为BC的中点,则
,
.
由于
,
,
是等腰直角三角形
(2)解:由于D,E分别为AB,AC的中点,
,即
.
故直线DE的斜率为
【分析】(1)根据A,B,C的坐标表示相应直线的斜率,根据两直线斜率之积为-1,两直线互相垂直,确定三角形的形状即可;
(2)根据三角形的中位线平行于第三边,结合平行线的斜率相等即可求出直线DE的斜率.
23.答案:
(1)解:由斜率公式得:
kAB=
=0,kAC=
=
,
所以直线AB的斜率为0,直线AC的斜率为
(2)解:如图所示:
由斜率公式可得kBC=
=
.
设直线CD的斜率为k,
结合图形可得当直线CD由CA的位置按逆时针方向旋转到CB的位置时,
直线CD与AB恒有交点,此时k由kCA增大到kCB
,
所以
即k的取值范围为
【分析】(1)根据题意结合已知条件利用直线斜率的坐标公式代入数值求出结果即可。(2)根据题意结合已知条件作出图像结合图形可得当直线CD由CA的位置按逆时针方向旋转到CB的位置时,直线CD与AB恒有交点进而得出k的取值范围。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
