人教版数学六年级下册:3.1.2 圆柱体的表面积 课件(共22张PPT)
文档属性
| 名称 | 人教版数学六年级下册:3.1.2 圆柱体的表面积 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-04 21:33:54 | ||
图片预览





文档简介
圆柱的表面积的应用
人教新课标版 小学六年级数学
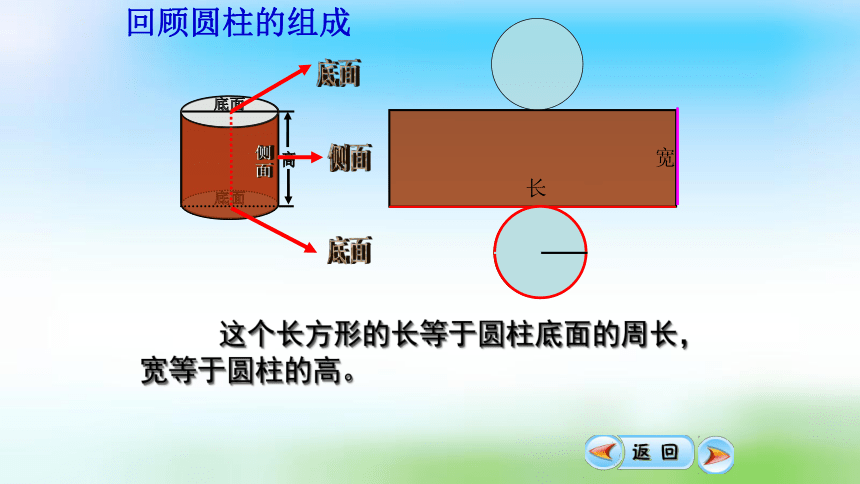
高
底面
侧
面
底面
底面
底面
侧面
长
宽
这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
回顾圆柱的组成
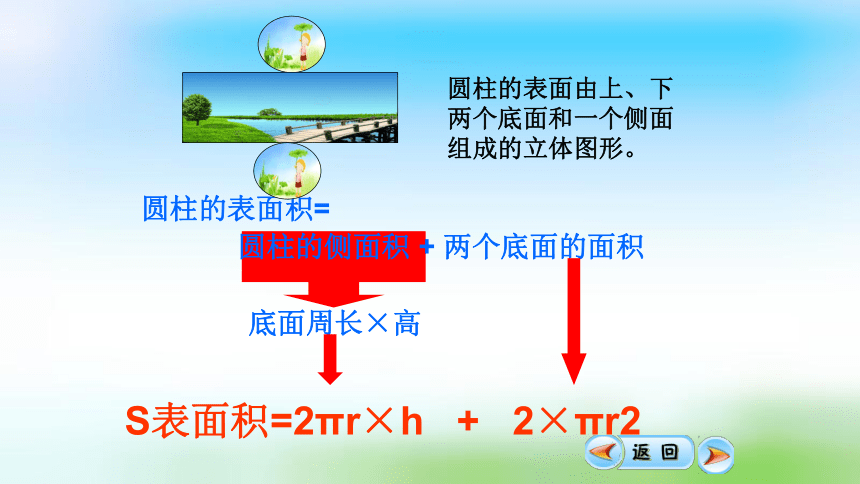
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
S表面积=2πr×h + 2×πr2
圆柱的表面由上、下两个底面和一个侧面组成的立体图形。
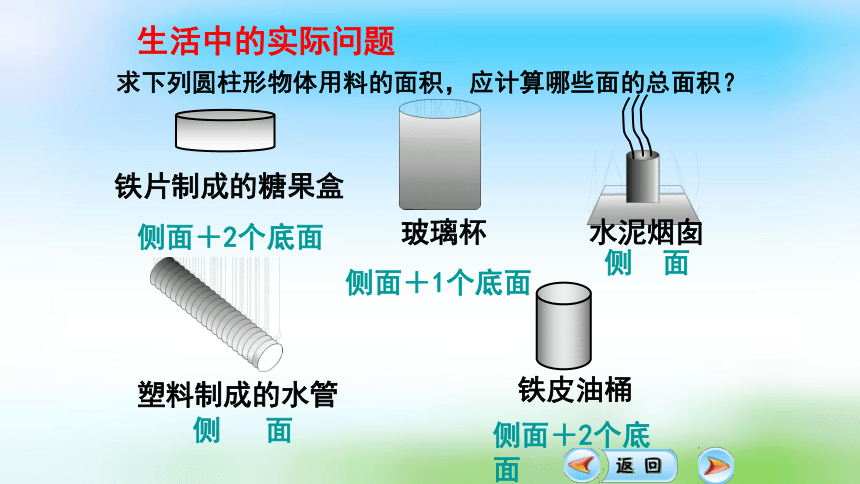
求下列圆柱形物体用料的面积,应计算哪些面的总面积?
铁片制成的糖果盒
玻璃杯
铁皮油桶
侧面+2个底面
侧 面
侧面+1个底面
侧 面
侧面+2个底面
塑料制成的水管
水泥烟囱
生活中的实际问题
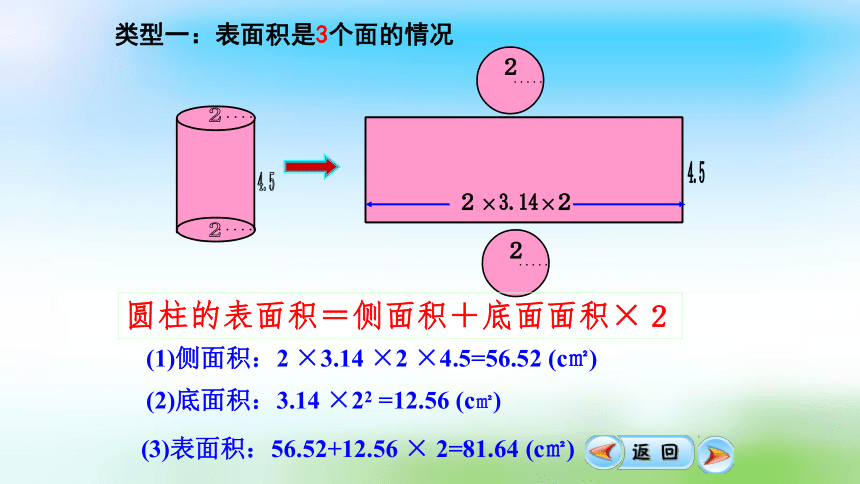
4.5
4.5
2
2
2
2
2
2
3.14
×
×
(1)侧面积:2 ×3.14 ×2 ×4.5=56.52 (c㎡)
(2)底面积:3.14 ×22 =12.56 (c㎡)
(3)表面积:56.52+12.56 × 2=81.64 (c㎡)
圆柱的表面积=侧面积+底面面积×2
类型一:表面积是3个面的情况
一个没有盖的圆柱形铁皮水桶,
高是24厘米,底面直径是20厘米,
做这个水桶要用铁皮多少平方厘米?
(得数保留整百)
(1)侧面积:
3.14×20×24=1507.2(平方厘米)
(2)底面积:3.14× =314(平方厘米)
(3)表面积:1507.2+314=1821.2
答:做这个水桶要用铁皮约1900平方厘米。
≈1900(平方厘米)
类型二:表面积是2个面的情况
类型三:表面积是1个面的情况
一台压路机的前轮是圆柱形,轮宽2m,直径1.2m.前轮转动一周,压路的面积是多少㎡?
3.14×1.2×2
=3.768×2
=7.536(㎡)
答:至少需要7.536 ㎡。
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
类型三:表面积增加几个面的情况
如图:一根长200厘米、底面直径是4厘米的圆柱形木料,把它锯成同样长的4段,表面积比原来增加了( )平方厘米。
增加的面积:3.14×2×2×6=75.36(平方厘米)
25.12
次数:4-1=3(次)
增加:3×2=6(个)
半径:4÷2=2(厘米)
此题增加的面积为圆柱6个底面圆的面积。
把一个底面直径为5厘米,高是8厘米的圆柱体沿底面直径切开,分成形状大小完全相同的两部分,它们的表面积比原来增加多少平方厘米?
8×5×2=80(平方厘米)
表面积增加了2个长方形的面积,
长方形的长相当于圆柱的高,
长方形的宽相当于圆柱的底面直径
此题增加的面积为2个长方形的面积。
类型四:表面积减少几个面的情况
将3个大小完全相同,长5厘米,底面半径3厘米的圆柱,拼成一个大的圆柱,表面积减少了多少平方厘米?
次数:3-1=2(次)
减少:2×2=4(个)
减少的面积:3.14×3×3×4=113.04(平方厘米)
此题减少的面积为4个圆柱底面员的面积。
如图,一段圆柱形木块截下5分米后,表面积减少了31.4平方分米,原来圆柱形木块的表面积是多少平方分米?
20
5
部分表面积减少的情况
5
如图,一段圆柱形木块截下5分米后,表面积减少了31.4平方分米,原来圆柱形木块的表面积是多少平方分米?
?
15
减少的表面积就是截去部分的
侧面积
如图,一段圆柱形木块截下5分米后,表面积减少了31.4平方分米,原来圆柱形木块的表面积是多少平方分米?
31.4÷5÷3.14÷2=1(分米)
2×3.14×1×20+3.14×12×2
=131.88(平方分米)
答:原来圆柱形木块的表面积是131.88平方分米。
减少的表面积就是截去部分的侧面积
李师傅把一根高1米的圆柱形木料,沿底面直径平均分成两部分,这时表面积比原来增加了0.8平方米。求这根木料原来的表面积。
(1)底面直径: 0.8 ÷2 ÷1=0.4 (米)
(2)圆柱的表面积:
3.14×(0.4÷2)×2+3.14×0.4×1
=0.2512+1.256
=1.5072(平方米)
答:这根木料原来的表面积是1.5072平方米。
部分表面积增加的情况
分两种情况:
1、以12.56厘米为底面周长, 6.28厘米为高。
2、以6.28厘米为底面周长 , 12.56厘米为高。
12.56
6.28
12.56
6.28
用一张长12.56厘米,宽6.28厘米的长方形纸卷成圆柱,并配上两个底面,它的表面积可能是多少?侧面积的大小相等吗?
半径:12.56÷3.14÷2=2(厘米)
S侧=12.56× 6.28 =78.8768(cm2)
S底=3.14 × 22=12.56(cm2)
S表=S侧+2S底=103.9968(cm2)
半径: 6.28÷3.14÷2=1(厘米)
S侧=12.56 × 6.28 =78.8768(cm2)
S底=3.14 × 12=3.14(cm2)
S表=S侧+2S底=85.1568(cm2)
类型五:卷成的情况
一个长方形沿一条直线旋转,会形成什么图形呢?
类型六:旋转的情况
以长为轴
10厘米
6厘米
以长为轴
以宽为轴
10厘米
6厘米
侧面积:2 ×3.14 ×6×10=376.8( cm2)
底面积:3.14 ×6×6=113.04( cm2)
表面积:376.8+113.04×2=602.88( cm2)
侧面积:2 ×3.14 ×10×6=376.8( cm2)
底面积:3.14 ×10×10=314( cm2)
表面积:376.8+314×2=1004.8( cm2)
类型六:旋转的情况
旋转也分为2种情况:
一种是以长方形的长为轴旋转,
另一种是以长方形的宽为轴旋转。
用一个棱长是6分米的正方体,削成一个最大的圆柱体,这个圆柱的表面积是多少?
表面积:113.04+28.26×2=169.56(平方分米)
正方体的棱长等于圆柱体的底面直径;
正方体的棱长等于圆柱体的高。
答:圆柱的表面积是169.56平方分米。
底面积:3.14×3×3=28.26(平方分米)
侧面积:3.14×6×6=113.04(平方分米)
半径: 6÷2=3(分米)
类型七:削成的情况
通过这节课的学习,
你有什么收获?有什么感受?
小结:
在解答实际问题前一定要
先进行分析,看它们求的
是哪部分面积,再选择解
答的方法。
再 见
人教新课标版 小学六年级数学
高
底面
侧
面
底面
底面
底面
侧面
长
宽
这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
回顾圆柱的组成
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
S表面积=2πr×h + 2×πr2
圆柱的表面由上、下两个底面和一个侧面组成的立体图形。
求下列圆柱形物体用料的面积,应计算哪些面的总面积?
铁片制成的糖果盒
玻璃杯
铁皮油桶
侧面+2个底面
侧 面
侧面+1个底面
侧 面
侧面+2个底面
塑料制成的水管
水泥烟囱
生活中的实际问题
4.5
4.5
2
2
2
2
2
2
3.14
×
×
(1)侧面积:2 ×3.14 ×2 ×4.5=56.52 (c㎡)
(2)底面积:3.14 ×22 =12.56 (c㎡)
(3)表面积:56.52+12.56 × 2=81.64 (c㎡)
圆柱的表面积=侧面积+底面面积×2
类型一:表面积是3个面的情况
一个没有盖的圆柱形铁皮水桶,
高是24厘米,底面直径是20厘米,
做这个水桶要用铁皮多少平方厘米?
(得数保留整百)
(1)侧面积:
3.14×20×24=1507.2(平方厘米)
(2)底面积:3.14× =314(平方厘米)
(3)表面积:1507.2+314=1821.2
答:做这个水桶要用铁皮约1900平方厘米。
≈1900(平方厘米)
类型二:表面积是2个面的情况
类型三:表面积是1个面的情况
一台压路机的前轮是圆柱形,轮宽2m,直径1.2m.前轮转动一周,压路的面积是多少㎡?
3.14×1.2×2
=3.768×2
=7.536(㎡)
答:至少需要7.536 ㎡。
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
类型三:表面积增加几个面的情况
如图:一根长200厘米、底面直径是4厘米的圆柱形木料,把它锯成同样长的4段,表面积比原来增加了( )平方厘米。
增加的面积:3.14×2×2×6=75.36(平方厘米)
25.12
次数:4-1=3(次)
增加:3×2=6(个)
半径:4÷2=2(厘米)
此题增加的面积为圆柱6个底面圆的面积。
把一个底面直径为5厘米,高是8厘米的圆柱体沿底面直径切开,分成形状大小完全相同的两部分,它们的表面积比原来增加多少平方厘米?
8×5×2=80(平方厘米)
表面积增加了2个长方形的面积,
长方形的长相当于圆柱的高,
长方形的宽相当于圆柱的底面直径
此题增加的面积为2个长方形的面积。
类型四:表面积减少几个面的情况
将3个大小完全相同,长5厘米,底面半径3厘米的圆柱,拼成一个大的圆柱,表面积减少了多少平方厘米?
次数:3-1=2(次)
减少:2×2=4(个)
减少的面积:3.14×3×3×4=113.04(平方厘米)
此题减少的面积为4个圆柱底面员的面积。
如图,一段圆柱形木块截下5分米后,表面积减少了31.4平方分米,原来圆柱形木块的表面积是多少平方分米?
20
5
部分表面积减少的情况
5
如图,一段圆柱形木块截下5分米后,表面积减少了31.4平方分米,原来圆柱形木块的表面积是多少平方分米?
?
15
减少的表面积就是截去部分的
侧面积
如图,一段圆柱形木块截下5分米后,表面积减少了31.4平方分米,原来圆柱形木块的表面积是多少平方分米?
31.4÷5÷3.14÷2=1(分米)
2×3.14×1×20+3.14×12×2
=131.88(平方分米)
答:原来圆柱形木块的表面积是131.88平方分米。
减少的表面积就是截去部分的侧面积
李师傅把一根高1米的圆柱形木料,沿底面直径平均分成两部分,这时表面积比原来增加了0.8平方米。求这根木料原来的表面积。
(1)底面直径: 0.8 ÷2 ÷1=0.4 (米)
(2)圆柱的表面积:
3.14×(0.4÷2)×2+3.14×0.4×1
=0.2512+1.256
=1.5072(平方米)
答:这根木料原来的表面积是1.5072平方米。
部分表面积增加的情况
分两种情况:
1、以12.56厘米为底面周长, 6.28厘米为高。
2、以6.28厘米为底面周长 , 12.56厘米为高。
12.56
6.28
12.56
6.28
用一张长12.56厘米,宽6.28厘米的长方形纸卷成圆柱,并配上两个底面,它的表面积可能是多少?侧面积的大小相等吗?
半径:12.56÷3.14÷2=2(厘米)
S侧=12.56× 6.28 =78.8768(cm2)
S底=3.14 × 22=12.56(cm2)
S表=S侧+2S底=103.9968(cm2)
半径: 6.28÷3.14÷2=1(厘米)
S侧=12.56 × 6.28 =78.8768(cm2)
S底=3.14 × 12=3.14(cm2)
S表=S侧+2S底=85.1568(cm2)
类型五:卷成的情况
一个长方形沿一条直线旋转,会形成什么图形呢?
类型六:旋转的情况
以长为轴
10厘米
6厘米
以长为轴
以宽为轴
10厘米
6厘米
侧面积:2 ×3.14 ×6×10=376.8( cm2)
底面积:3.14 ×6×6=113.04( cm2)
表面积:376.8+113.04×2=602.88( cm2)
侧面积:2 ×3.14 ×10×6=376.8( cm2)
底面积:3.14 ×10×10=314( cm2)
表面积:376.8+314×2=1004.8( cm2)
类型六:旋转的情况
旋转也分为2种情况:
一种是以长方形的长为轴旋转,
另一种是以长方形的宽为轴旋转。
用一个棱长是6分米的正方体,削成一个最大的圆柱体,这个圆柱的表面积是多少?
表面积:113.04+28.26×2=169.56(平方分米)
正方体的棱长等于圆柱体的底面直径;
正方体的棱长等于圆柱体的高。
答:圆柱的表面积是169.56平方分米。
底面积:3.14×3×3=28.26(平方分米)
侧面积:3.14×6×6=113.04(平方分米)
半径: 6÷2=3(分米)
类型七:削成的情况
通过这节课的学习,
你有什么收获?有什么感受?
小结:
在解答实际问题前一定要
先进行分析,看它们求的
是哪部分面积,再选择解
答的方法。
再 见
