北师大版八年级数学上册 4.4一次函数的应用同步练习题(word版含答案)
文档属性
| 名称 | 北师大版八年级数学上册 4.4一次函数的应用同步练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 80.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 15:52:58 | ||
图片预览




文档简介
北师大版八年级数学上册
4.4借助一次函数表达式解决一些简单问题同步练习题
一、选择题
1.如图,某正比例函数的图象经过点M(-2,1),则此正比例函数的表达式为(
)
A.y=-x
B.y=x
C.y=-2x
D.y=2x
2.如图,直线对应的函数表达式是(
)
A.y=-2x-2
B.y=2x+2
C.y=-2x+2
D.y=2x-2
3.已知一次函数y=kx+3的图象经过点A(1,2),则其表达式为(
)
A.y=-x+3
B.y=-x+3
C.y=x+3
D.y=x+3
4.生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,并画出如图所示的图象(CD∥x轴),该植物最高的高度是(
)
A.50
cm
B.20
cm
C.16
cm
D.12
cm
5.已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么k,b的值分别是(
)
x
-2
-1
0
1
2
3
y
3
2
1
0
-1
-2
A.1,1
B.1,-1
C.-1,1
D.-1,-1
6.如图,一次函数y=x+6的图象与x轴,y轴分别交于点A,B,过点B的直线l平分△ABO的面积,则直线l相应的函数表达式为(
)
A.y=x+6
B.y=x+6
C.y=x+6
D.y=x+6
二、填空题
7.一次函数y=bx+2的图象经过点A(-1,1),则b=
.
8.已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为-2,且当x=2时,y=1,那么此函数的表达式为
.
9.一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶前往B地.下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时
0
1
2
2.5
余油量y/升
100
80
60
50
则y与x的函数关系式为
,自变量x的取值范围为
.
10.已知一次函数y=kx+b的图象经过点A(1,3)且和y=2x-3平行,则函数表达式为
.
11.如图1,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2中的图象,则至少需要
s能把小水杯注满.
12.已知直线y=kx+b经过点A(-2,0)和y轴正半轴上的一点B,若△ABO(O为坐标原点)的面积为2,则b的值为
.
13.如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的函数表达式为
.
三、解答题
14.已知y与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)求x=-5时y的值.
15.根据记录,从地面向上11
km以内,每升高1
km,气温降低6
℃;又知在距离地面11
km以上高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11
km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26
℃时,飞机距离地面的高度为7
km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12
km的高空,飞机外的气温是多少摄氏度呢?请求出假如当时飞机距离地面12
km时,飞机外的气温.
16.已知金属棒的长度l(cm)是温度t(℃)的一次函数.现有一根金属棒,在0
℃时的长度是200
cm,温度每升高1
℃,它就伸长0.002
cm.
(1)求这根金属棒的长度l与温度t的函数关系式;
(2)当温度为100
℃时,求这根金属棒的长度;
(3)当这根金属棒加热后长度伸长到201.6
cm时,求金属棒的温度.
17.如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标,点B的横坐标如图所示.
(1)求直线AB的表达式;
(2)在直线AB上,是否存在点P使得△AOP的面积为1?如果存在,请直接写出所有满足条件的点P的坐标.
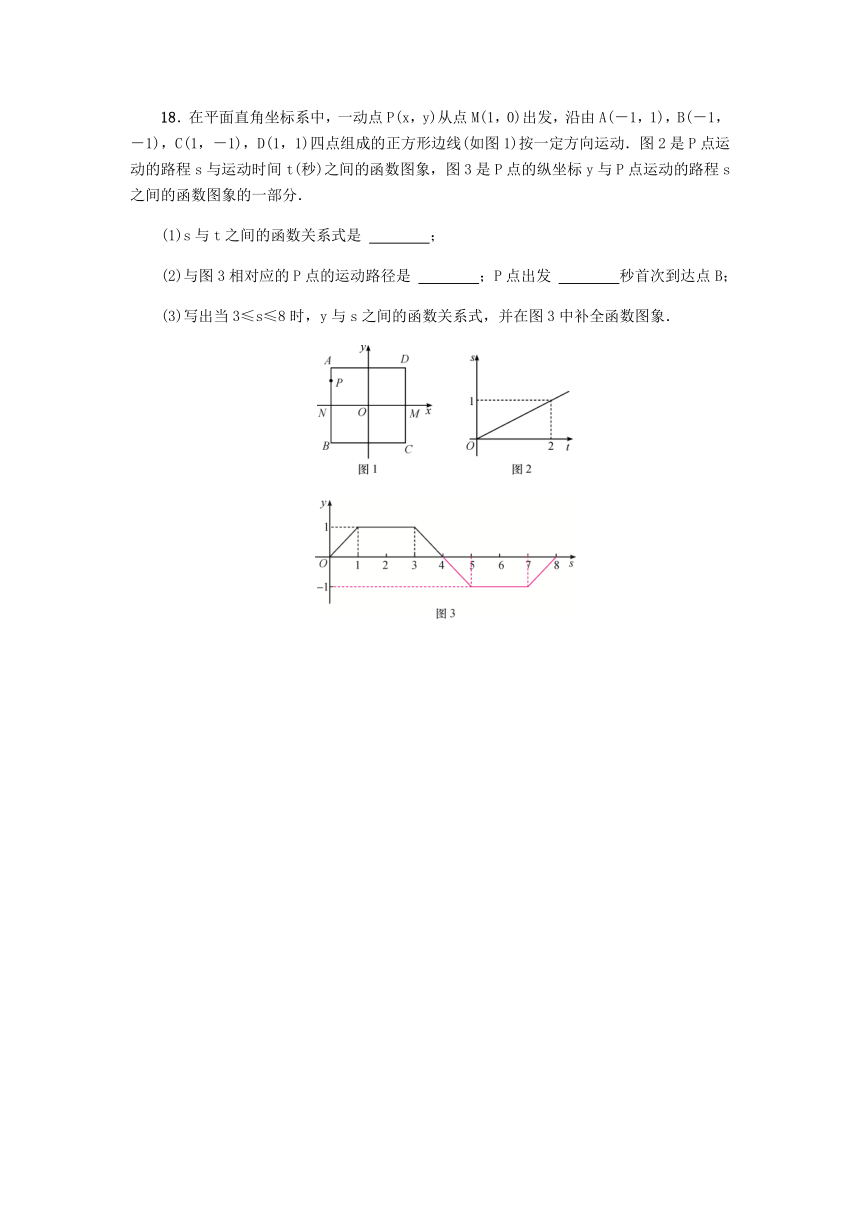
18.在平面直角坐标系中,一动点P(x,y)从点M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图1)按一定方向运动.图2是P点运动的路程s与运动时间t(秒)之间的函数图象,图3是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(1)s与t之间的函数关系式是
;
(2)与图3相对应的P点的运动路径是
;P点出发
秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图3中补全函数图象.
参考答案
一、选择题
1.如图,某正比例函数的图象经过点M(-2,1),则此正比例函数的表达式为(A)
A.y=-x
B.y=x
C.y=-2x
D.y=2x
2.如图,直线对应的函数表达式是(B)
A.y=-2x-2
B.y=2x+2
C.y=-2x+2
D.y=2x-2
3.已知一次函数y=kx+3的图象经过点A(1,2),则其表达式为(B)
A.y=-x+3
B.y=-x+3
C.y=x+3
D.y=x+3
4.生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,并画出如图所示的图象(CD∥x轴),该植物最高的高度是(C)
A.50
cm
B.20
cm
C.16
cm
D.12
cm
5.已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么k,b的值分别是(C)
x
-2
-1
0
1
2
3
y
3
2
1
0
-1
-2
A.1,1
B.1,-1
C.-1,1
D.-1,-1
6.如图,一次函数y=x+6的图象与x轴,y轴分别交于点A,B,过点B的直线l平分△ABO的面积,则直线l相应的函数表达式为(D)
A.y=x+6
B.y=x+6
C.y=x+6
D.y=x+6
二、填空题
7.一次函数y=bx+2的图象经过点A(-1,1),则b=1.
8.已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为-2,且当x=2时,y=1,那么此函数的表达式为y=x-2.
9.一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶前往B地.下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时
0
1
2
2.5
余油量y/升
100
80
60
50
则y与x的函数关系式为y=-20x+100,自变量x的取值范围为0≤x≤5.
10.已知一次函数y=kx+b的图象经过点A(1,3)且和y=2x-3平行,则函数表达式为y=2x+1.
11.如图1,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2中的图象,则至少需要5s能把小水杯注满.
12.已知直线y=kx+b经过点A(-2,0)和y轴正半轴上的一点B,若△ABO(O为坐标原点)的面积为2,则b的值为2.
13.如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的函数表达式为y=-x+1.
三、解答题
14.已知y与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)求x=-5时y的值.
解:(1)设y=k(x-1),把x=3,y=4代入,得
(3-1)k=4,解得k=2.
所以y=2(x-1),即y=2x-2.
(2)当x=-5时,y=2×(-5)-2=-12.
15.根据记录,从地面向上11
km以内,每升高1
km,气温降低6
℃;又知在距离地面11
km以上高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11
km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26
℃时,飞机距离地面的高度为7
km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12
km的高空,飞机外的气温是多少摄氏度呢?请求出假如当时飞机距离地面12
km时,飞机外的气温.
解:(1)y=m-6x.
(2)将x=7,y=-26代入y=m-6x,得
-26=m-42,所以m=16.
所以当时地面气温为16
℃.
因为x=12>11,
所以y=16-6×11=-50.
故假如当时飞机距离地面12
km时,飞机外的气温为-50
℃.
16.已知金属棒的长度l(cm)是温度t(℃)的一次函数.现有一根金属棒,在0
℃时的长度是200
cm,温度每升高1
℃,它就伸长0.002
cm.
(1)求这根金属棒的长度l与温度t的函数关系式;
(2)当温度为100
℃时,求这根金属棒的长度;
(3)当这根金属棒加热后长度伸长到201.6
cm时,求金属棒的温度.
解:(1)设l与t的函数关系式为l=kt+b.
将(0,200)代入,得b=200.
又由温度每升高1
℃,它就伸长0.002
cm,得k=0.002.
所以金属棒的长度l与温度t的函数关系式为l=0.002t+200.
(2)将t=100代入函数关系式,得l=0.002×100+200=200.2.
所以当温度为100
℃时,这根金属棒的长度是200.2
cm.
(3)令l=201.6,代入函数关系式,得
t==800.
所以金属棒的温度为800
℃.
17.如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标,点B的横坐标如图所示.
(1)求直线AB的表达式;
(2)在直线AB上,是否存在点P使得△AOP的面积为1?如果存在,请直接写出所有满足条件的点P的坐标.
解:(1)根据题意,得点A的坐标为(0,2),点B的坐标为(4,0),
设直线AB的表达式为y=kx+b,
把A(0,2),B(4,0)代入y=kx+b,得
b=2①,0=4k+b②,将①代入②,得k=-.
所以直线AB的表达式为y=-x+2.
(2)设点P的横坐标为a,根据题意,得
S△AOP=OA·|a|=|a|=1,
解得a=1或a=-1.
当a=1时,y=-×1+2=;
当a=-1时,y=-×(-1)+2=.
则点P的坐标为(1,)或(-1,).
18.在平面直角坐标系中,一动点P(x,y)从点M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图1)按一定方向运动.图2是P点运动的路程s与运动时间t(秒)之间的函数图象,图3是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(1)s与t之间的函数关系式是s=t(t≥0);
(2)与图3相对应的P点的运动路径是M→D→A→N;P点出发10秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图3中补全函数图象.
解:当3≤s<5,即P从A到B时,y=4-s;
当5≤s<7,即P从B到C时,y=-1;
当7≤s≤8,即P从C到M时,y=s-8.
补全图形如图.
4.4借助一次函数表达式解决一些简单问题同步练习题
一、选择题
1.如图,某正比例函数的图象经过点M(-2,1),则此正比例函数的表达式为(
)
A.y=-x
B.y=x
C.y=-2x
D.y=2x
2.如图,直线对应的函数表达式是(
)
A.y=-2x-2
B.y=2x+2
C.y=-2x+2
D.y=2x-2
3.已知一次函数y=kx+3的图象经过点A(1,2),则其表达式为(
)
A.y=-x+3
B.y=-x+3
C.y=x+3
D.y=x+3
4.生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,并画出如图所示的图象(CD∥x轴),该植物最高的高度是(
)
A.50
cm
B.20
cm
C.16
cm
D.12
cm
5.已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么k,b的值分别是(
)
x
-2
-1
0
1
2
3
y
3
2
1
0
-1
-2
A.1,1
B.1,-1
C.-1,1
D.-1,-1
6.如图,一次函数y=x+6的图象与x轴,y轴分别交于点A,B,过点B的直线l平分△ABO的面积,则直线l相应的函数表达式为(
)
A.y=x+6
B.y=x+6
C.y=x+6
D.y=x+6
二、填空题
7.一次函数y=bx+2的图象经过点A(-1,1),则b=
.
8.已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为-2,且当x=2时,y=1,那么此函数的表达式为
.
9.一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶前往B地.下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时
0
1
2
2.5
余油量y/升
100
80
60
50
则y与x的函数关系式为
,自变量x的取值范围为
.
10.已知一次函数y=kx+b的图象经过点A(1,3)且和y=2x-3平行,则函数表达式为
.
11.如图1,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2中的图象,则至少需要
s能把小水杯注满.
12.已知直线y=kx+b经过点A(-2,0)和y轴正半轴上的一点B,若△ABO(O为坐标原点)的面积为2,则b的值为
.
13.如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的函数表达式为
.
三、解答题
14.已知y与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)求x=-5时y的值.
15.根据记录,从地面向上11
km以内,每升高1
km,气温降低6
℃;又知在距离地面11
km以上高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11
km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26
℃时,飞机距离地面的高度为7
km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12
km的高空,飞机外的气温是多少摄氏度呢?请求出假如当时飞机距离地面12
km时,飞机外的气温.
16.已知金属棒的长度l(cm)是温度t(℃)的一次函数.现有一根金属棒,在0
℃时的长度是200
cm,温度每升高1
℃,它就伸长0.002
cm.
(1)求这根金属棒的长度l与温度t的函数关系式;
(2)当温度为100
℃时,求这根金属棒的长度;
(3)当这根金属棒加热后长度伸长到201.6
cm时,求金属棒的温度.
17.如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标,点B的横坐标如图所示.
(1)求直线AB的表达式;
(2)在直线AB上,是否存在点P使得△AOP的面积为1?如果存在,请直接写出所有满足条件的点P的坐标.
18.在平面直角坐标系中,一动点P(x,y)从点M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图1)按一定方向运动.图2是P点运动的路程s与运动时间t(秒)之间的函数图象,图3是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(1)s与t之间的函数关系式是
;
(2)与图3相对应的P点的运动路径是
;P点出发
秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图3中补全函数图象.
参考答案
一、选择题
1.如图,某正比例函数的图象经过点M(-2,1),则此正比例函数的表达式为(A)
A.y=-x
B.y=x
C.y=-2x
D.y=2x
2.如图,直线对应的函数表达式是(B)
A.y=-2x-2
B.y=2x+2
C.y=-2x+2
D.y=2x-2
3.已知一次函数y=kx+3的图象经过点A(1,2),则其表达式为(B)
A.y=-x+3
B.y=-x+3
C.y=x+3
D.y=x+3
4.生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,并画出如图所示的图象(CD∥x轴),该植物最高的高度是(C)
A.50
cm
B.20
cm
C.16
cm
D.12
cm
5.已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么k,b的值分别是(C)
x
-2
-1
0
1
2
3
y
3
2
1
0
-1
-2
A.1,1
B.1,-1
C.-1,1
D.-1,-1
6.如图,一次函数y=x+6的图象与x轴,y轴分别交于点A,B,过点B的直线l平分△ABO的面积,则直线l相应的函数表达式为(D)
A.y=x+6
B.y=x+6
C.y=x+6
D.y=x+6
二、填空题
7.一次函数y=bx+2的图象经过点A(-1,1),则b=1.
8.已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为-2,且当x=2时,y=1,那么此函数的表达式为y=x-2.
9.一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶前往B地.下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时
0
1
2
2.5
余油量y/升
100
80
60
50
则y与x的函数关系式为y=-20x+100,自变量x的取值范围为0≤x≤5.
10.已知一次函数y=kx+b的图象经过点A(1,3)且和y=2x-3平行,则函数表达式为y=2x+1.
11.如图1,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2中的图象,则至少需要5s能把小水杯注满.
12.已知直线y=kx+b经过点A(-2,0)和y轴正半轴上的一点B,若△ABO(O为坐标原点)的面积为2,则b的值为2.
13.如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的函数表达式为y=-x+1.
三、解答题
14.已知y与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)求x=-5时y的值.
解:(1)设y=k(x-1),把x=3,y=4代入,得
(3-1)k=4,解得k=2.
所以y=2(x-1),即y=2x-2.
(2)当x=-5时,y=2×(-5)-2=-12.
15.根据记录,从地面向上11
km以内,每升高1
km,气温降低6
℃;又知在距离地面11
km以上高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11
km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26
℃时,飞机距离地面的高度为7
km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12
km的高空,飞机外的气温是多少摄氏度呢?请求出假如当时飞机距离地面12
km时,飞机外的气温.
解:(1)y=m-6x.
(2)将x=7,y=-26代入y=m-6x,得
-26=m-42,所以m=16.
所以当时地面气温为16
℃.
因为x=12>11,
所以y=16-6×11=-50.
故假如当时飞机距离地面12
km时,飞机外的气温为-50
℃.
16.已知金属棒的长度l(cm)是温度t(℃)的一次函数.现有一根金属棒,在0
℃时的长度是200
cm,温度每升高1
℃,它就伸长0.002
cm.
(1)求这根金属棒的长度l与温度t的函数关系式;
(2)当温度为100
℃时,求这根金属棒的长度;
(3)当这根金属棒加热后长度伸长到201.6
cm时,求金属棒的温度.
解:(1)设l与t的函数关系式为l=kt+b.
将(0,200)代入,得b=200.
又由温度每升高1
℃,它就伸长0.002
cm,得k=0.002.
所以金属棒的长度l与温度t的函数关系式为l=0.002t+200.
(2)将t=100代入函数关系式,得l=0.002×100+200=200.2.
所以当温度为100
℃时,这根金属棒的长度是200.2
cm.
(3)令l=201.6,代入函数关系式,得
t==800.
所以金属棒的温度为800
℃.
17.如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标,点B的横坐标如图所示.
(1)求直线AB的表达式;
(2)在直线AB上,是否存在点P使得△AOP的面积为1?如果存在,请直接写出所有满足条件的点P的坐标.
解:(1)根据题意,得点A的坐标为(0,2),点B的坐标为(4,0),
设直线AB的表达式为y=kx+b,
把A(0,2),B(4,0)代入y=kx+b,得
b=2①,0=4k+b②,将①代入②,得k=-.
所以直线AB的表达式为y=-x+2.
(2)设点P的横坐标为a,根据题意,得
S△AOP=OA·|a|=|a|=1,
解得a=1或a=-1.
当a=1时,y=-×1+2=;
当a=-1时,y=-×(-1)+2=.
则点P的坐标为(1,)或(-1,).
18.在平面直角坐标系中,一动点P(x,y)从点M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图1)按一定方向运动.图2是P点运动的路程s与运动时间t(秒)之间的函数图象,图3是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(1)s与t之间的函数关系式是s=t(t≥0);
(2)与图3相对应的P点的运动路径是M→D→A→N;P点出发10秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图3中补全函数图象.
解:当3≤s<5,即P从A到B时,y=4-s;
当5≤s<7,即P从B到C时,y=-1;
当7≤s≤8,即P从C到M时,y=s-8.
补全图形如图.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
