北师大版八年级数学上册4.4一次函数的应用同步练习题(word版含答案)(3)
文档属性
| 名称 | 北师大版八年级数学上册4.4一次函数的应用同步练习题(word版含答案)(3) |  | |
| 格式 | zip | ||
| 文件大小 | 236.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 15:52:23 | ||
图片预览



文档简介
北师大版八年级数学上册第三章
4.4借助单个一次函数图象解决简单实际问题
同步练习题
一、选择题
1.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.如图表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分钟)变化的函数图象,则每分钟乙比甲多行驶的路程是(
)
A.0.5千米
B.1千米
C.1.5千米
D.2千米
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列说法中错误的是(
)
A.客车比出租车晚4小时到达目的地
B.客车速度为60千米/时,出租车速度为100千米/时
C.两车出发后3.75小时相遇
D.两车相遇时客车距乙地还有225千米
3.A,B两地相距20
km,甲、乙两人沿同一条路线从A地到B地.如图反映的是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:
①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4
h到达目的地;③乙比甲先出发1
h;④甲在出发4
h后被乙追上.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
4.如图是某电信公司提供的A,B两种方案的移动通信费用y(元)与通话时间x(分钟)之间的关系,则下列结论中正确的有(
)
①若通话时间少于120分钟,则A方案比B方案便宜;
②若通话时间超过200分钟,则B方案比A方案便宜;
③若通信费用为60元,则B方案比A方案的通话时间长;
④当通话时间为170分钟时,A方案与B方案的费用相等.
A.1个
B.2个
C.3个
D.4个
5.一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程y(km)与时间t(h)的函数图象如图所示,下列说法正确的有(
)
①快车追上慢车需6
h;②慢车比快车早出发2
h;③快车速度为46
km/h;④慢车速度为46
km/h;⑤AB两地相距828
km.
A.2个 B.3个 C.4个 D.5个
二、填空题
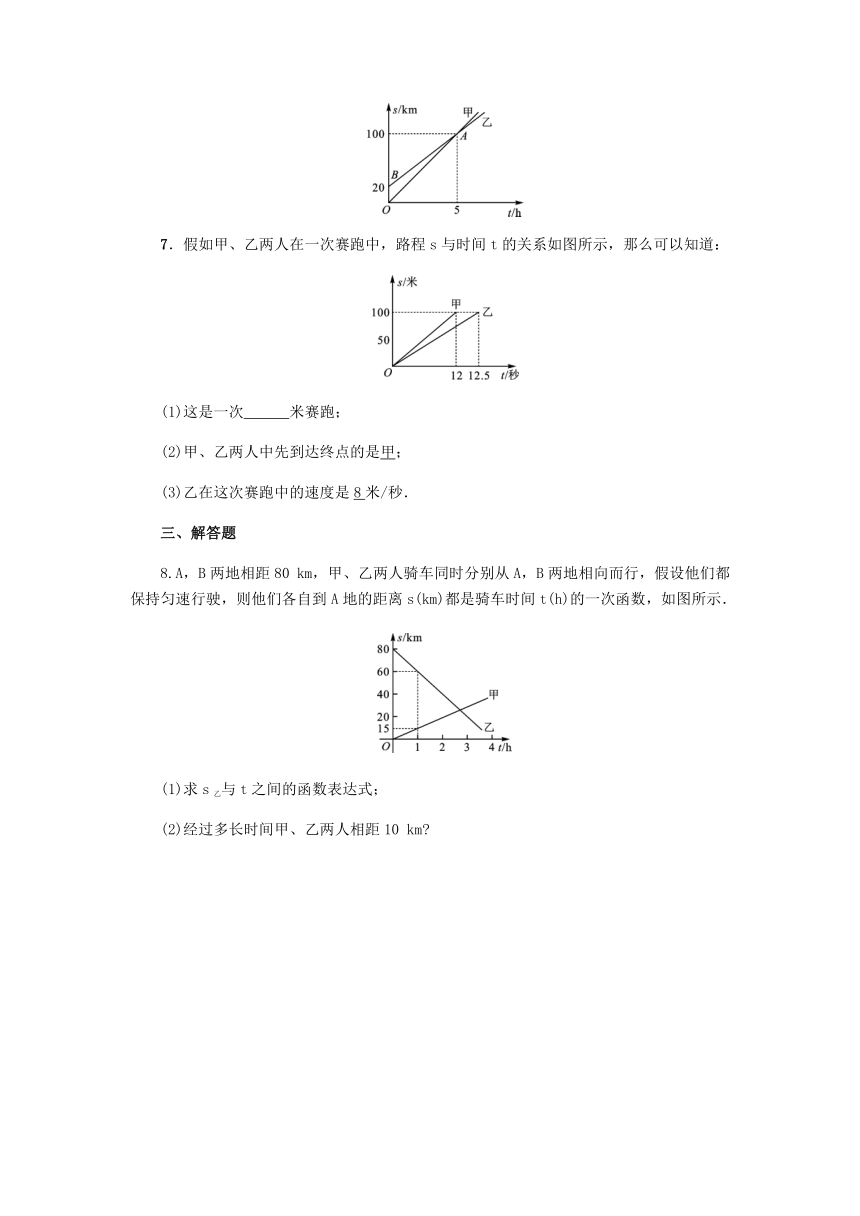
6.如图,射线OA,BA分别表示甲、乙两人骑自行车运动时的行驶路程s(km)与时间t(h)之间的函数关系图象,则这两人骑自行车的速度相差
km/h.
7.假如甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,那么可以知道:
(1)这是一次
米赛跑;
(2)甲、乙两人中先到达终点的是甲;
(3)乙在这次赛跑中的速度是8米/秒.
三、解答题
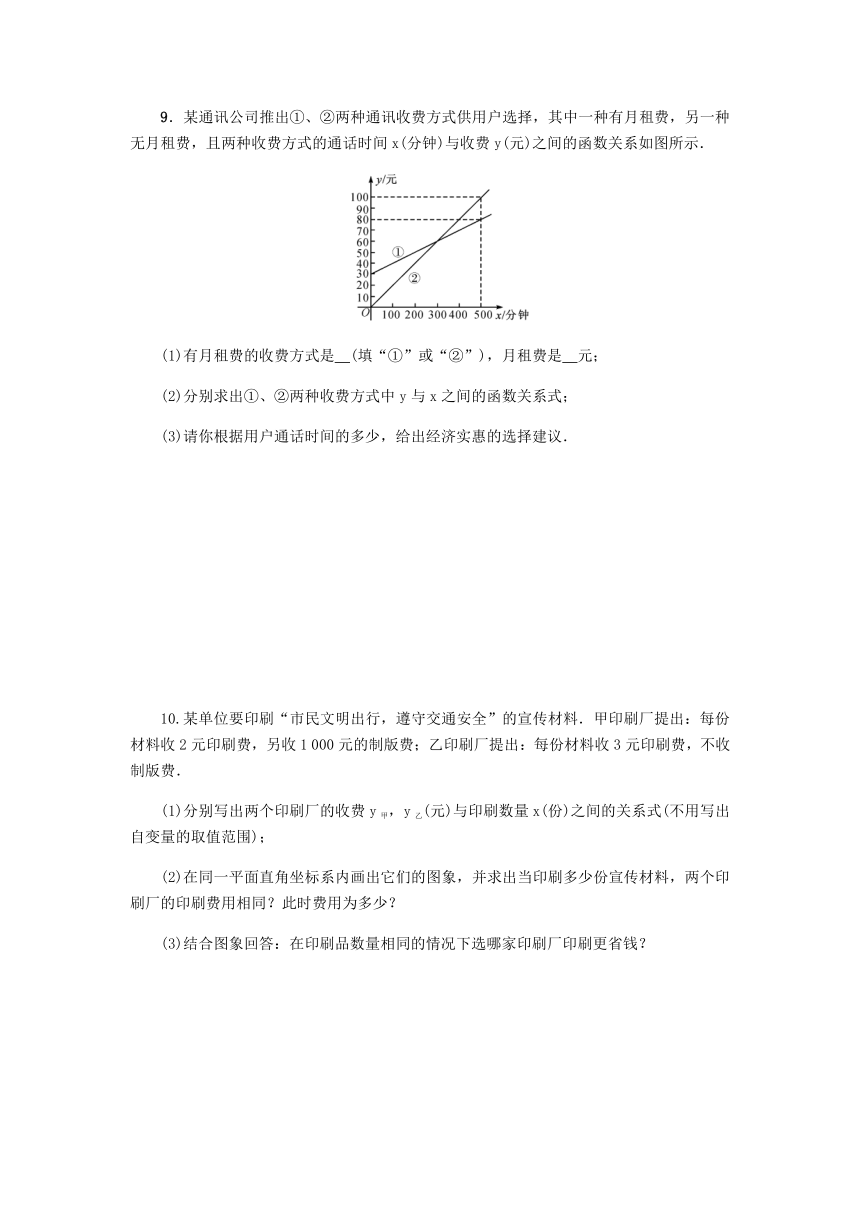
8.A,B两地相距80
km,甲、乙两人骑车同时分别从A,B两地相向而行,假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t(h)的一次函数,如图所示.
(1)求s乙与t之间的函数表达式;
(2)经过多长时间甲、乙两人相距10
km?
9.某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通话时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)有月租费的收费方式是
(填“①”或“②”),月租费是
元;
(2)分别求出①、②两种收费方式中y与x之间的函数关系式;
(3)请你根据用户通话时间的多少,给出经济实惠的选择建议.
10.某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1
000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y甲,y乙(元)与印刷数量x(份)之间的关系式(不用写出自变量的取值范围);
(2)在同一平面直角坐标系内画出它们的图象,并求出当印刷多少份宣传材料,两个印刷厂的印刷费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印刷更省钱?
11.某中学九年级甲、乙两班商定举行一次远足活动,A,B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.两班同时出发,相向而行.设步行时间为x(小时),甲、乙两班离A地的距离(千米)分别为y1,y2,y1,y2与x的函数关系图象如图所示.根据图象解答下列问题:
(1)直接写出y1,y2与x的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?相遇时乙班离A地多少千米?
(3)甲、乙两班首次相距4千米时所用时间是小时.
12.甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲场所有商品按8折出售,乙商场对一次购物中超过200元后的部分打7折.
(1)以x(元)表示商品原价,y(元)表示购物金额,分别就两家商场的让利方式,写出y关于x的函数表达式;
(2)在同一平面直角坐标系中画出(1)中函数的图象;
(3)春节期间选择哪家商场购物更省钱?
13.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(图1).图2中l1,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分钟)之间的关系.根据图象回答问题:
(1)哪一条线表示B到海岸的距离与追赶时间的关系?
(2)求出l1,l2的函数关系式;
(3)当A逃到离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?
14.某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km)计算,甲汽车租赁公司的月租费为y1(元),乙汽车租赁公司的月租费为y2(元).如果y1,y2与x之间的函数关系如图,那么:
(1)分别求出y1,y2与x之间的函数关系式;
(2)每月用车路程在什么范围内,租用甲汽车租赁公司的车所需费用较少?
(3)如果每月用车的路程约2
500
km,那么租用哪家公司的车所需费用较少?
参考答案
一、选择题
1.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.如图表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分钟)变化的函数图象,则每分钟乙比甲多行驶的路程是(A)
A.0.5千米
B.1千米
C.1.5千米
D.2千米
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列说法中错误的是(D)
A.客车比出租车晚4小时到达目的地
B.客车速度为60千米/时,出租车速度为100千米/时
C.两车出发后3.75小时相遇
D.两车相遇时客车距乙地还有225千米
3.A,B两地相距20
km,甲、乙两人沿同一条路线从A地到B地.如图反映的是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:
①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4
h到达目的地;③乙比甲先出发1
h;④甲在出发4
h后被乙追上.其中正确的有(A)
A.1个
B.2个
C.3个
D.4个
4.如图是某电信公司提供的A,B两种方案的移动通信费用y(元)与通话时间x(分钟)之间的关系,则下列结论中正确的有(D)
①若通话时间少于120分钟,则A方案比B方案便宜;
②若通话时间超过200分钟,则B方案比A方案便宜;
③若通信费用为60元,则B方案比A方案的通话时间长;
④当通话时间为170分钟时,A方案与B方案的费用相等.
A.1个
B.2个
C.3个
D.4个
5.一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程y(km)与时间t(h)的函数图象如图所示,下列说法正确的有(B)
①快车追上慢车需6
h;②慢车比快车早出发2
h;③快车速度为46
km/h;④慢车速度为46
km/h;⑤AB两地相距828
km.
A.2个 B.3个 C.4个 D.5个
二、填空题
6.如图,射线OA,BA分别表示甲、乙两人骑自行车运动时的行驶路程s(km)与时间t(h)之间的函数关系图象,则这两人骑自行车的速度相差4
km/h.
7.假如甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,那么可以知道:
(1)这是一次100米赛跑;
(2)甲、乙两人中先到达终点的是甲;
(3)乙在这次赛跑中的速度是8米/秒.
三、解答题
8.A,B两地相距80
km,甲、乙两人骑车同时分别从A,B两地相向而行,假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t(h)的一次函数,如图所示.
(1)求s乙与t之间的函数表达式;
(2)经过多长时间甲、乙两人相距10
km?
解:(1)设s乙与t之间的函数表达式为s乙=kt+80,
将点(1,60)代入,解得k=-20.
故s乙与t之间的表达式为s乙=-20t+80.
(2)同理可求得s甲与t之间的函数表达式为s甲=15t,
由题意,得|s甲-s乙|=10,
即|15t-(-20t+80)|=10.
解得t=2或.
答:经过2或
h甲、乙两人相距10
km.
9.某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通话时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)有月租费的收费方式是①(填“①”或“②”),月租费是30元;
(2)分别求出①、②两种收费方式中y与x之间的函数关系式;
(3)请你根据用户通话时间的多少,给出经济实惠的选择建议.
解:(2)设收费方式①中y与x之间的函数关系式为y1=k1x+30,收费方式②中y与x之间的函数关系式为y2=k2x,由题意,得
500k1+30=80,解得k1=0.1.
500k2=100,解得k2=0.2.
故所求的关系式为y1=0.1x+30,y2=0.2x.
(3)由y1=y2,得0.1x+30=0.2x,解得x=300.
故由图可知,当通话时间在300分钟内,选择通讯收费方式②实惠;当通话时间超过300分钟时,选择通讯收费方式①实惠;当通话时间为300分钟时,选择通讯收费方式①、②一样实惠.
10.某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1
000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y甲,y乙(元)与印刷数量x(份)之间的关系式(不用写出自变量的取值范围);
(2)在同一平面直角坐标系内画出它们的图象,并求出当印刷多少份宣传材料,两个印刷厂的印刷费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印刷更省钱?
解:(1)y甲=2x+1
000,y乙=3x.
(2)图象如图所示.
当y甲=y乙时,可得2x+1
000=3x.
解得x=1
000.则y甲=y乙=3
000.
所以当印刷1
000份品数量时费用相等,为3
000元.
(3)由图象可知:当印刷品数量不足1
000份时,选择乙印刷厂省钱;
当印刷品数量为1
000份时,两家费用都一样;
当印刷宣传材料超过1
000份时,选择甲印刷厂省钱.
11.某中学九年级甲、乙两班商定举行一次远足活动,A,B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.两班同时出发,相向而行.设步行时间为x(小时),甲、乙两班离A地的距离(千米)分别为y1,y2,y1,y2与x的函数关系图象如图所示.根据图象解答下列问题:
(1)直接写出y1,y2与x的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?相遇时乙班离A地多少千米?
(3)甲、乙两班首次相距4千米时所用时间是小时.
解:(1)y1=4x,y2=-5x+10.
(2)令4x=-5x+10,
解得x=.
当x=时,
y2=-5×+10=.
所以甲、乙两班学生出发后,小时相遇,相遇时乙班离A地为千米.
12.甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲场所有商品按8折出售,乙商场对一次购物中超过200元后的部分打7折.
(1)以x(元)表示商品原价,y(元)表示购物金额,分别就两家商场的让利方式,写出y关于x的函数表达式;
(2)在同一平面直角坐标系中画出(1)中函数的图象;
(3)春节期间选择哪家商场购物更省钱?
解:(1)甲商场:y=0.8x(x≥0);
乙商场:y=
(2)如图所示.
(3)令0.8x=0.7x+60,解得x=600,结合函数图象可知:当x<600时,选甲商场购物更省钱;当x=600时,甲、乙两商场购物花钱相同;当x>600时,选乙商场购物更省钱.
13.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(图1).图2中l1,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分钟)之间的关系.根据图象回答问题:
(1)哪一条线表示B到海岸的距离与追赶时间的关系?
(2)求出l1,l2的函数关系式;
(3)当A逃到离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?
解:(1)当t=0时,B距海岸0海里,即s=0,
故l1表示B到海岸的距离与追赶时间的关系.
(2)设l1的函数关系式为s=kt,将点(10,5)代入,得
5=10k,解得k=0.5.
所以l1的函数关系式为s=0.5t.
设l2的函数关系式为s=at+5,将点(10,7)代入,得
7=10a+5,解得a=0.2.
所以l2的函数关系式为s=0.2t+5.
(3)令0.5t=0.2t+5,解得t=.
因为0.2×+5=<12,
所以B能在A逃入公海前将其拦截.
14.某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km)计算,甲汽车租赁公司的月租费为y1(元),乙汽车租赁公司的月租费为y2(元).如果y1,y2与x之间的函数关系如图,那么:
(1)分别求出y1,y2与x之间的函数关系式;
(2)每月用车路程在什么范围内,租用甲汽车租赁公司的车所需费用较少?
(3)如果每月用车的路程约2
500
km,那么租用哪家公司的车所需费用较少?
解:(1)设y1=kx+b.根据题意,得b=1
000,①
2
000k+b=2
000.②
将①代入②,得2
000k+1
000=2
000,解得k=.
所以y1=x+1
000.
设y2=ax.由图象可知,y2经过点(2
000,2
000),则2
000a=2
000,解得a=1.所以y2=x.
(2)根据图象可知,路程在2
000
km以上时,y1在y2的下方,此时租用甲公司费用较少.
(3)因为2
500>2
000,
所以租用甲公司所需费用较少.
4.4借助单个一次函数图象解决简单实际问题
同步练习题
一、选择题
1.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.如图表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分钟)变化的函数图象,则每分钟乙比甲多行驶的路程是(
)
A.0.5千米
B.1千米
C.1.5千米
D.2千米
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列说法中错误的是(
)
A.客车比出租车晚4小时到达目的地
B.客车速度为60千米/时,出租车速度为100千米/时
C.两车出发后3.75小时相遇
D.两车相遇时客车距乙地还有225千米
3.A,B两地相距20
km,甲、乙两人沿同一条路线从A地到B地.如图反映的是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:
①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4
h到达目的地;③乙比甲先出发1
h;④甲在出发4
h后被乙追上.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
4.如图是某电信公司提供的A,B两种方案的移动通信费用y(元)与通话时间x(分钟)之间的关系,则下列结论中正确的有(
)
①若通话时间少于120分钟,则A方案比B方案便宜;
②若通话时间超过200分钟,则B方案比A方案便宜;
③若通信费用为60元,则B方案比A方案的通话时间长;
④当通话时间为170分钟时,A方案与B方案的费用相等.
A.1个
B.2个
C.3个
D.4个
5.一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程y(km)与时间t(h)的函数图象如图所示,下列说法正确的有(
)
①快车追上慢车需6
h;②慢车比快车早出发2
h;③快车速度为46
km/h;④慢车速度为46
km/h;⑤AB两地相距828
km.
A.2个 B.3个 C.4个 D.5个
二、填空题
6.如图,射线OA,BA分别表示甲、乙两人骑自行车运动时的行驶路程s(km)与时间t(h)之间的函数关系图象,则这两人骑自行车的速度相差
km/h.
7.假如甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,那么可以知道:
(1)这是一次
米赛跑;
(2)甲、乙两人中先到达终点的是甲;
(3)乙在这次赛跑中的速度是8米/秒.
三、解答题
8.A,B两地相距80
km,甲、乙两人骑车同时分别从A,B两地相向而行,假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t(h)的一次函数,如图所示.
(1)求s乙与t之间的函数表达式;
(2)经过多长时间甲、乙两人相距10
km?
9.某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通话时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)有月租费的收费方式是
(填“①”或“②”),月租费是
元;
(2)分别求出①、②两种收费方式中y与x之间的函数关系式;
(3)请你根据用户通话时间的多少,给出经济实惠的选择建议.
10.某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1
000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y甲,y乙(元)与印刷数量x(份)之间的关系式(不用写出自变量的取值范围);
(2)在同一平面直角坐标系内画出它们的图象,并求出当印刷多少份宣传材料,两个印刷厂的印刷费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印刷更省钱?
11.某中学九年级甲、乙两班商定举行一次远足活动,A,B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.两班同时出发,相向而行.设步行时间为x(小时),甲、乙两班离A地的距离(千米)分别为y1,y2,y1,y2与x的函数关系图象如图所示.根据图象解答下列问题:
(1)直接写出y1,y2与x的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?相遇时乙班离A地多少千米?
(3)甲、乙两班首次相距4千米时所用时间是小时.
12.甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲场所有商品按8折出售,乙商场对一次购物中超过200元后的部分打7折.
(1)以x(元)表示商品原价,y(元)表示购物金额,分别就两家商场的让利方式,写出y关于x的函数表达式;
(2)在同一平面直角坐标系中画出(1)中函数的图象;
(3)春节期间选择哪家商场购物更省钱?
13.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(图1).图2中l1,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分钟)之间的关系.根据图象回答问题:
(1)哪一条线表示B到海岸的距离与追赶时间的关系?
(2)求出l1,l2的函数关系式;
(3)当A逃到离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?
14.某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km)计算,甲汽车租赁公司的月租费为y1(元),乙汽车租赁公司的月租费为y2(元).如果y1,y2与x之间的函数关系如图,那么:
(1)分别求出y1,y2与x之间的函数关系式;
(2)每月用车路程在什么范围内,租用甲汽车租赁公司的车所需费用较少?
(3)如果每月用车的路程约2
500
km,那么租用哪家公司的车所需费用较少?
参考答案
一、选择题
1.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.如图表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分钟)变化的函数图象,则每分钟乙比甲多行驶的路程是(A)
A.0.5千米
B.1千米
C.1.5千米
D.2千米
2.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列说法中错误的是(D)
A.客车比出租车晚4小时到达目的地
B.客车速度为60千米/时,出租车速度为100千米/时
C.两车出发后3.75小时相遇
D.两车相遇时客车距乙地还有225千米
3.A,B两地相距20
km,甲、乙两人沿同一条路线从A地到B地.如图反映的是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:
①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4
h到达目的地;③乙比甲先出发1
h;④甲在出发4
h后被乙追上.其中正确的有(A)
A.1个
B.2个
C.3个
D.4个
4.如图是某电信公司提供的A,B两种方案的移动通信费用y(元)与通话时间x(分钟)之间的关系,则下列结论中正确的有(D)
①若通话时间少于120分钟,则A方案比B方案便宜;
②若通话时间超过200分钟,则B方案比A方案便宜;
③若通信费用为60元,则B方案比A方案的通话时间长;
④当通话时间为170分钟时,A方案与B方案的费用相等.
A.1个
B.2个
C.3个
D.4个
5.一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程y(km)与时间t(h)的函数图象如图所示,下列说法正确的有(B)
①快车追上慢车需6
h;②慢车比快车早出发2
h;③快车速度为46
km/h;④慢车速度为46
km/h;⑤AB两地相距828
km.
A.2个 B.3个 C.4个 D.5个
二、填空题
6.如图,射线OA,BA分别表示甲、乙两人骑自行车运动时的行驶路程s(km)与时间t(h)之间的函数关系图象,则这两人骑自行车的速度相差4
km/h.
7.假如甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,那么可以知道:
(1)这是一次100米赛跑;
(2)甲、乙两人中先到达终点的是甲;
(3)乙在这次赛跑中的速度是8米/秒.
三、解答题
8.A,B两地相距80
km,甲、乙两人骑车同时分别从A,B两地相向而行,假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t(h)的一次函数,如图所示.
(1)求s乙与t之间的函数表达式;
(2)经过多长时间甲、乙两人相距10
km?
解:(1)设s乙与t之间的函数表达式为s乙=kt+80,
将点(1,60)代入,解得k=-20.
故s乙与t之间的表达式为s乙=-20t+80.
(2)同理可求得s甲与t之间的函数表达式为s甲=15t,
由题意,得|s甲-s乙|=10,
即|15t-(-20t+80)|=10.
解得t=2或.
答:经过2或
h甲、乙两人相距10
km.
9.某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通话时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)有月租费的收费方式是①(填“①”或“②”),月租费是30元;
(2)分别求出①、②两种收费方式中y与x之间的函数关系式;
(3)请你根据用户通话时间的多少,给出经济实惠的选择建议.
解:(2)设收费方式①中y与x之间的函数关系式为y1=k1x+30,收费方式②中y与x之间的函数关系式为y2=k2x,由题意,得
500k1+30=80,解得k1=0.1.
500k2=100,解得k2=0.2.
故所求的关系式为y1=0.1x+30,y2=0.2x.
(3)由y1=y2,得0.1x+30=0.2x,解得x=300.
故由图可知,当通话时间在300分钟内,选择通讯收费方式②实惠;当通话时间超过300分钟时,选择通讯收费方式①实惠;当通话时间为300分钟时,选择通讯收费方式①、②一样实惠.
10.某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1
000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y甲,y乙(元)与印刷数量x(份)之间的关系式(不用写出自变量的取值范围);
(2)在同一平面直角坐标系内画出它们的图象,并求出当印刷多少份宣传材料,两个印刷厂的印刷费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印刷更省钱?
解:(1)y甲=2x+1
000,y乙=3x.
(2)图象如图所示.
当y甲=y乙时,可得2x+1
000=3x.
解得x=1
000.则y甲=y乙=3
000.
所以当印刷1
000份品数量时费用相等,为3
000元.
(3)由图象可知:当印刷品数量不足1
000份时,选择乙印刷厂省钱;
当印刷品数量为1
000份时,两家费用都一样;
当印刷宣传材料超过1
000份时,选择甲印刷厂省钱.
11.某中学九年级甲、乙两班商定举行一次远足活动,A,B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.两班同时出发,相向而行.设步行时间为x(小时),甲、乙两班离A地的距离(千米)分别为y1,y2,y1,y2与x的函数关系图象如图所示.根据图象解答下列问题:
(1)直接写出y1,y2与x的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?相遇时乙班离A地多少千米?
(3)甲、乙两班首次相距4千米时所用时间是小时.
解:(1)y1=4x,y2=-5x+10.
(2)令4x=-5x+10,
解得x=.
当x=时,
y2=-5×+10=.
所以甲、乙两班学生出发后,小时相遇,相遇时乙班离A地为千米.
12.甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲场所有商品按8折出售,乙商场对一次购物中超过200元后的部分打7折.
(1)以x(元)表示商品原价,y(元)表示购物金额,分别就两家商场的让利方式,写出y关于x的函数表达式;
(2)在同一平面直角坐标系中画出(1)中函数的图象;
(3)春节期间选择哪家商场购物更省钱?
解:(1)甲商场:y=0.8x(x≥0);
乙商场:y=
(2)如图所示.
(3)令0.8x=0.7x+60,解得x=600,结合函数图象可知:当x<600时,选甲商场购物更省钱;当x=600时,甲、乙两商场购物花钱相同;当x>600时,选乙商场购物更省钱.
13.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(图1).图2中l1,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分钟)之间的关系.根据图象回答问题:
(1)哪一条线表示B到海岸的距离与追赶时间的关系?
(2)求出l1,l2的函数关系式;
(3)当A逃到离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?
解:(1)当t=0时,B距海岸0海里,即s=0,
故l1表示B到海岸的距离与追赶时间的关系.
(2)设l1的函数关系式为s=kt,将点(10,5)代入,得
5=10k,解得k=0.5.
所以l1的函数关系式为s=0.5t.
设l2的函数关系式为s=at+5,将点(10,7)代入,得
7=10a+5,解得a=0.2.
所以l2的函数关系式为s=0.2t+5.
(3)令0.5t=0.2t+5,解得t=.
因为0.2×+5=<12,
所以B能在A逃入公海前将其拦截.
14.某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km)计算,甲汽车租赁公司的月租费为y1(元),乙汽车租赁公司的月租费为y2(元).如果y1,y2与x之间的函数关系如图,那么:
(1)分别求出y1,y2与x之间的函数关系式;
(2)每月用车路程在什么范围内,租用甲汽车租赁公司的车所需费用较少?
(3)如果每月用车的路程约2
500
km,那么租用哪家公司的车所需费用较少?
解:(1)设y1=kx+b.根据题意,得b=1
000,①
2
000k+b=2
000.②
将①代入②,得2
000k+1
000=2
000,解得k=.
所以y1=x+1
000.
设y2=ax.由图象可知,y2经过点(2
000,2
000),则2
000a=2
000,解得a=1.所以y2=x.
(2)根据图象可知,路程在2
000
km以上时,y1在y2的下方,此时租用甲公司费用较少.
(3)因为2
500>2
000,
所以租用甲公司所需费用较少.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
