弧、弦、圆心角学案

《弧、弦、圆心角》教学案
学习目标：
结合图形让了解圆心角的概念，学会辨别圆心角。
2.发现圆心角、弦、弧之间的相等关系，并初步学会运用这些关系解决有关问题。
预习导学：
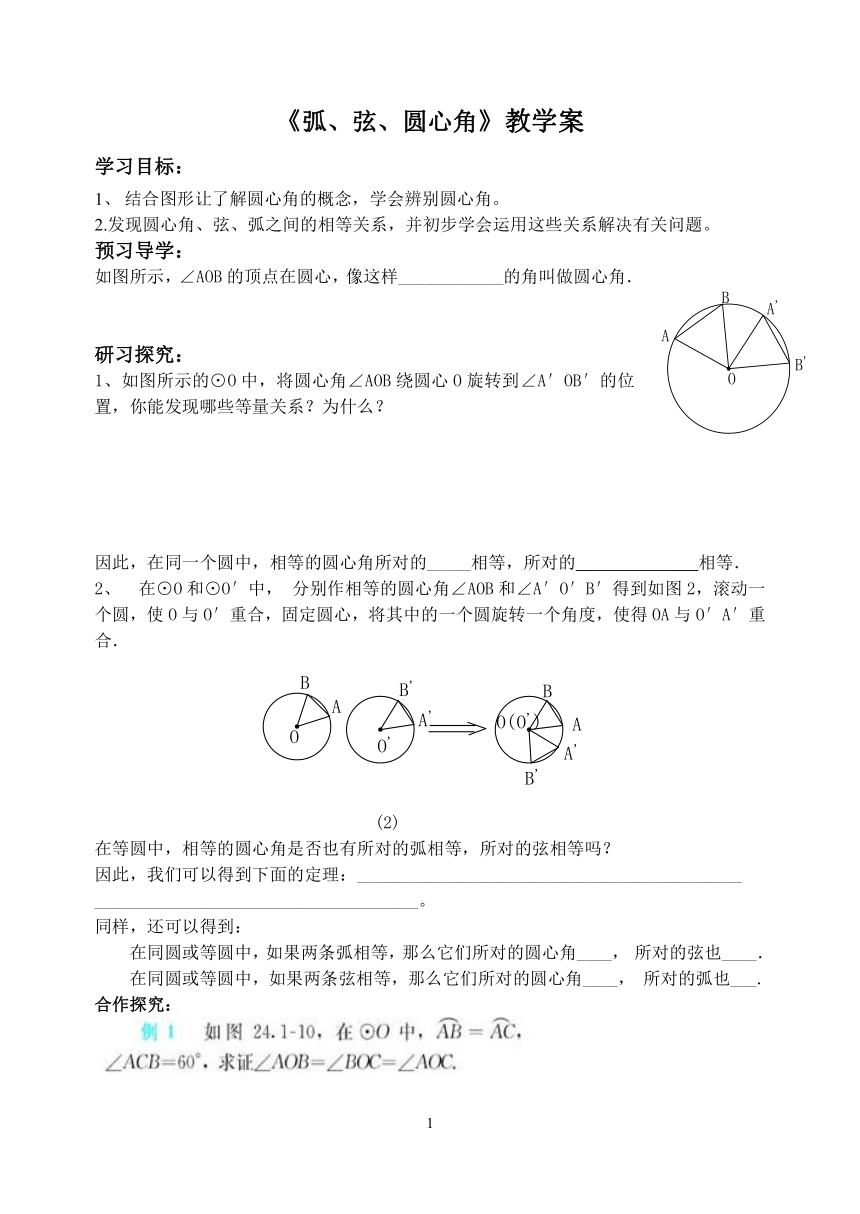
如图所示，∠AOB的顶点在圆心，像这样____________的角叫做圆心角．
研习探究：
1、如图所示的⊙O中，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置，你能发现哪些等量关系？为什么？
因此，在同一个圆中，相等的圆心角所对的_____相等，所对的__ ___相等．
2、 在⊙O和⊙O′中，分别作相等的圆心角∠AOB和∠A′O′B′得到如图2，滚动一个圆，使O与O′重合，固定圆心，将其中的一个圆旋转一个角度，使得OA与O′A′重合．
(2)
在等圆中，相等的圆心角是否也有所对的弧相等，所对的弦相等吗？
因此，我们可以得到下面的定理：____________________________________________
_____________________________________。
同样，还可以得到：
在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角____，所对的弦也____．
在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角____，所对的弧也___.
合作探究：
例2 如图，在⊙O中，AB、CD是两条弦，OE⊥AB，OF⊥CD，垂足分别为EF．
（1）如果∠AOB=∠COD，那么OE与OF的大小有什么关系？为什么？
（2）如果OE=OF，那么弧AB与弧CD的大小有什么关系？AB与CD的大小有什么关系？为什么？∠AOB与∠COD呢？
巩固练习：
教材P83 练习1、2
达标检测
1．如果两个圆心角相等，那么（ ）
A．这两个圆心角所对的弦相等;B．这两个圆心角所对的弧相等
C．这两个圆心角所对的弦的弦心距相等;D．以上说法都不对
2．在同圆中，圆心角∠AOB=2∠COD，则两条弧AB与CD关系是（ ）
A．=2 B．> C．<2 D．不能确定 ．
3.一条弦长恰好为半径长，则此弦所对的弧是半圆的_________．
4．如图2，AB和DE是⊙O的直径，弦AC∥DE，若弦BE=3，则弦CE=________．
PAGE
2