7青岛版(第一章 特殊四边形单元检测)创新学案(文及答案)
文档属性
| 名称 | 7青岛版(第一章 特殊四边形单元检测)创新学案(文及答案) |  | |
| 格式 | zip | ||
| 文件大小 | 190.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-13 23:49:04 | ||
图片预览

文档简介
第一章 特殊四边形单元检测
(时间120分钟 满分120分)
班级_______姓名__________等级__________
一、选择题(每小题3分,共30分)
1.(2009黑龙江牡丹江)下列图形中既是轴对称图形又是中心对称图形的是( )
2.以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
3.顺次连接等腰梯形四边中点所得四边形是( )
A.菱形 B.正方形 C.矩形 D.等腰梯形
4.如图1-1,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A. B. C. D.
图1-1 图1-2 图1-3 图1-4
5.(2009广东茂名)图1-2杨伯家小院子的四棵小树刚好在其梯形院子各边的中点上,若在四边形种上小草,则这块草地的形状是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
6.如图1-3,下列条件之一能使是菱形的为( )
① ② ③ ④
A.①③ B.②③ C.③④ D.①②③
7.(2009山东济宁)如图图1-4,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A. B. C. D.
8. 将矩形纸片ABCD按如图1-5所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )
A.1 B.2 C. D.
图1-5 图1-6
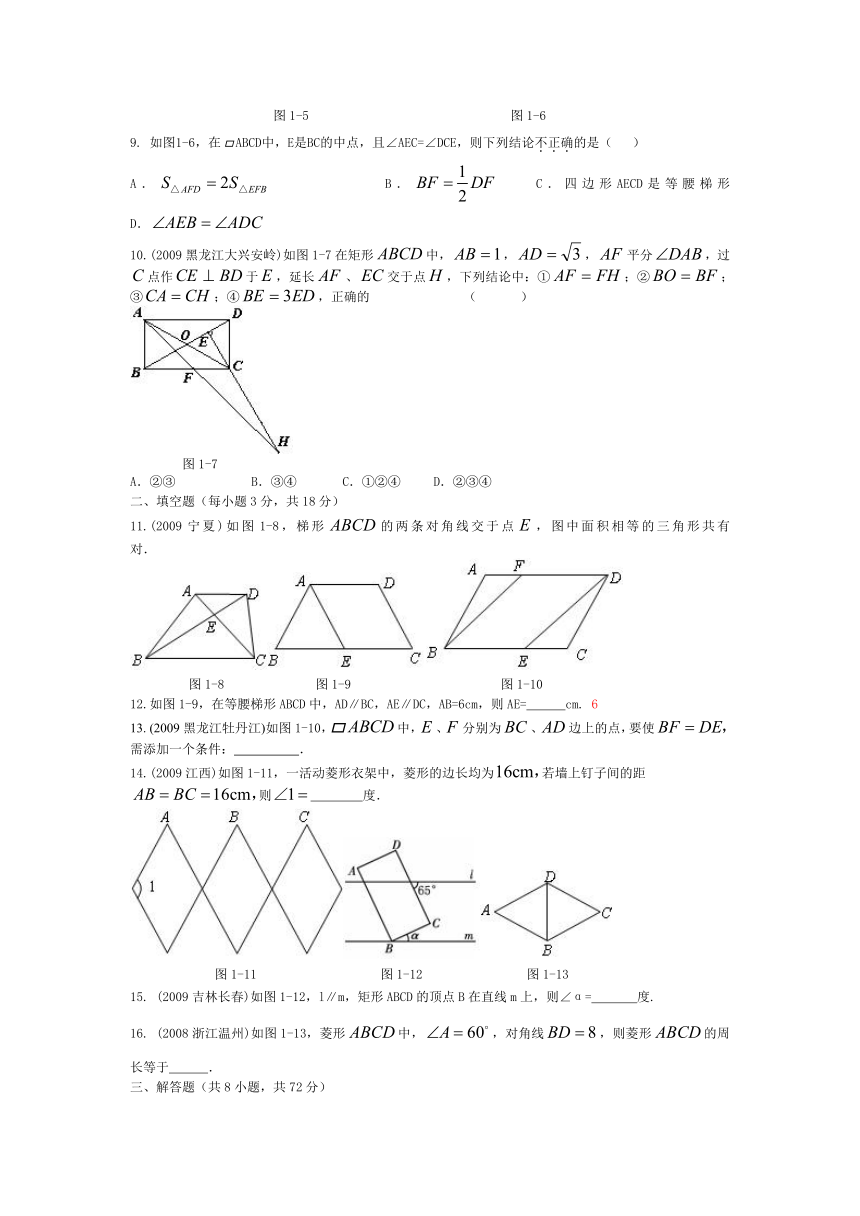
9. 如图1-6,在ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
A. B. C.四边形AECD是等腰梯形 D.
10.(2009黑龙江大兴安岭)如图1-7在矩形中,,,平分,过点作于,延长、交于点,下列结论中:①;②;③;④,正确的 ( )
图1-7
A.②③ B.③④ C.①②④ D.②③④
二、填空题(每小题3分,共18分)
11.(2009宁夏)如图1-8,梯形的两条对角线交于点,图中面积相等的三角形共有 对.
图1-8 图1-9 图1-10
12.如图1-9,在等腰梯形ABCD中,AD∥BC,AE∥DC,AB=6cm,则AE= cm. 6
13. (2009黑龙江牡丹江)如图1-10,中,、分别为、边上的点,要使需添加一个条件: .
14.(2009江西)如图1-11,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距则 度.
图1-11 图1-12 图1-13
15. (2009吉林长春)如图1-12,l∥m,矩形ABCD的顶点B在直线m上,则∠α= 度.
16. (2008浙江温州)如图1-13,菱形中,,对角线,则菱形的周长等于 .
三、解答题(共8小题,共72分)
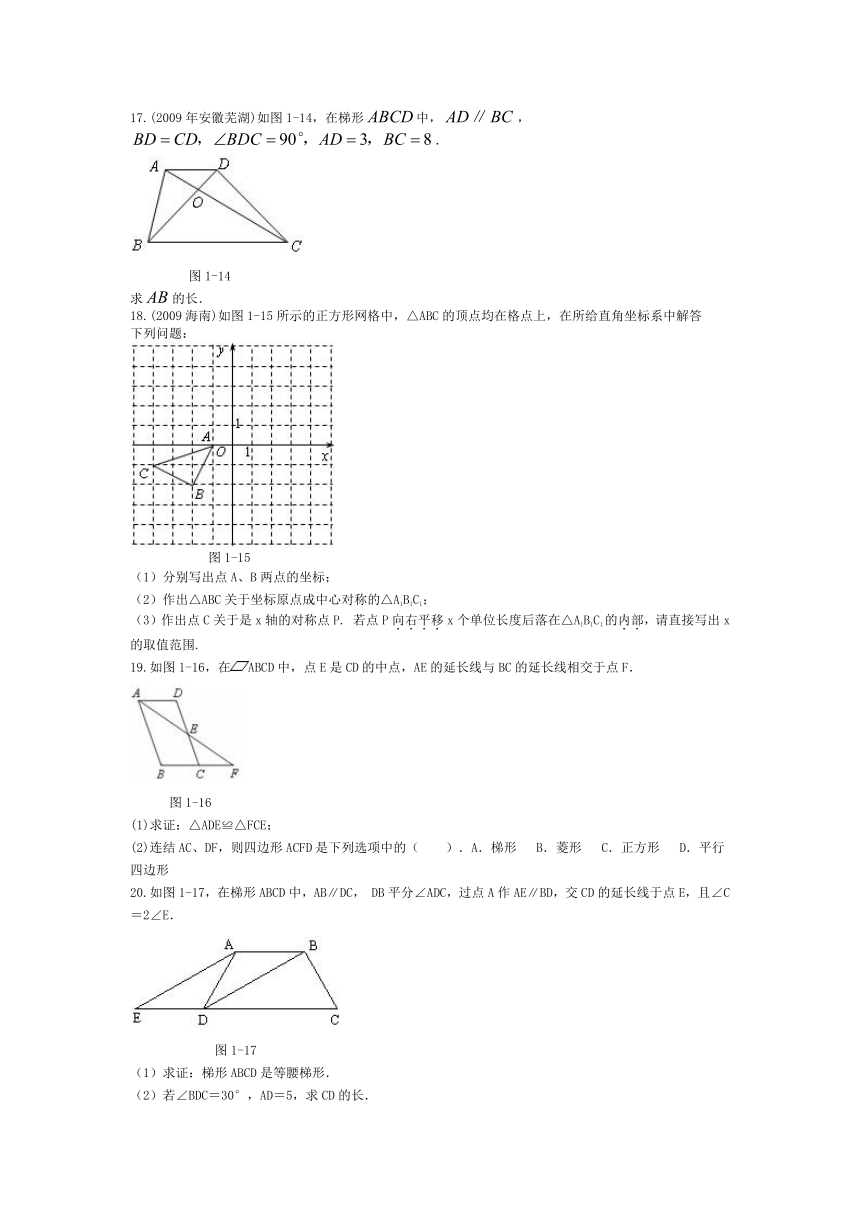
17.(2009年安徽芜湖)如图1-14,在梯形中,,
.
图1-14
求的长.
18.(2009海南)如图1-15所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答
下列问题:
图1-15
(1)分别写出点A、B两点的坐标;
(2)作出△ABC关于坐标原点成中心对称的△A1B1C1;
(3)作出点C关于是x轴的对称点P. 若点P向右平移x个单位长度后落在△A1B1C1的内部,请直接写出x的取值范围.
19.如图1-16,在ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F.
图1-16
(1)求证:△ADE≌△FCE;
(2)连结AC、DF,则四边形ACFD是下列选项中的( ).A.梯形 B.菱形 C.正方形 D.平行四边形
20.如图1-17,在梯形ABCD中,AB∥DC, DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
图1-17
(1)求证:梯形ABCD是等腰梯形.
(2)若∠BDC=30°,AD=5,求CD的长.
21.如图1-18,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC,交BC的延长线于F。
图1-18
请你猜想DE与DF的大小有什么关系?并证明你的猜想
22.如图1-19,在△ABC中,∠A、∠B的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.
(1)点D是△ABC的________心;
(2)求证:四边形DECF为菱形.
23.如图1-20,在梯形中,,,,于点E,F是CD的中点,DG是梯形的高.
图1-20
(1)求证:四边形AEFD是平行四边形;
(2)设,四边形DEGF的面积为y,求y关于x的函数关系式.
24.已知:如图1-21所示的一张矩形纸片(),将纸片折叠一次,使点与重合,再展开,折痕交边于,交边于,分别连结和.
图1-21
(1)求证:四边形是菱形;
(2)若,的面积为,求的周长;
(3)在线段上是否存在一点,使得?若存在,请说明点的位置,并予以证明;若不存在,请说明理由.
第一章 特殊四边形单元检测答案
一、1.B 2.C 3.A 4.B 5.A 6.A 7.C 8.D 9.A 10.D
二、11.3 12.6 13.
14.120 15.25 16.32
三、17.解:作于于
四边形是矩形.
是的边上的中线.
在中,
18.(1)A、B两点的坐标分别为(-1,0)、(-2,-2);
(2)所作△A1B1C1如图所示;
(3)所作点P如上图所示,5.5 < x <8 .
19.证明:(1) ∵ 四边形ABCD是平行四边形,∴ AD∥BF,∴ ∠D=∠ECF.
∵ E是CD的中点,∴ DE = CE.又 ∠AED=∠FEC, ∴ △ADE≌△FCE.
(2) D.或填“平行四边形”.
20.(1)证明:∵AE∥BD, ∴∠E=∠BDC
∵DB平分∠ADC ∴∠ADC=2∠BDC
又∵∠C=2∠E∴∠ADC=∠BCD∴梯形ABCD是等腰梯形
(2)解:由第(1)问,得∠C=2∠E=2∠BDC=60°,且BC=AD=5
∵ 在△BCD中,∠C=60°, ∠BDC=30°∴∠DBC=90°∴DC=2BC=10
21.解:DE=DF
证明如下:连结BD
∵四边形ABCD是菱形 ∴∠CBD=∠ABD(菱形的对角线平分一组对角)
∵DF⊥BC,DE⊥AB ∴DF=DE(角平分线上的点到角两边的距离相等)
22.(1) 内.
(2) 证明:连接CD,
∵ DE∥AC,DF∥BC, ∴ 四边形DECF为平行四边形,
又∵ 点D是△ABC的内心, ∴ CD平分∠ACB,即∠FCD=∠ECD,
又∠FDC=∠ECD,∴ ∠FCD=∠FDC ∴ FC=FD, ∴ □DECF为菱形.
23.(1) 证明: ∵,∴梯形ABCD为等腰梯形.∵∠C=60°,∴,
又∵,∴.∴.∴.
由已知,∴AE∥DC.
又∵AE为等腰三角形ABD的高, ∴E是BD的中点, ∵F是DC的中点, ∴EF∥BC. ∴EF∥AD.
∴四边形AEFD是平行四边形.
(2)解:在Rt△AED中, ,∵,∴.
在Rt△DGC中 ∠C=60°,并且,∴.
由(1)知: 在平行四边形AEFD中,又∵,∴,
∴四边形DEGF的面积,
∴ .
24.解:(1)连结交于,
当顶点与重合时,折痕垂直平分,
,
在平行四边形中,,
,
.
四边形是菱形.
(2)四边形是菱形,.
设,,,
①
又,则. ②
由①、②得:
,(不合题意舍去)
的周长为.
(3)过作交于,则就是所求的点.
证明:由作法,,
由(1)得:,又,
,
,则
四边形是菱形,,.
(时间120分钟 满分120分)
班级_______姓名__________等级__________
一、选择题(每小题3分,共30分)
1.(2009黑龙江牡丹江)下列图形中既是轴对称图形又是中心对称图形的是( )
2.以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
3.顺次连接等腰梯形四边中点所得四边形是( )
A.菱形 B.正方形 C.矩形 D.等腰梯形
4.如图1-1,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A. B. C. D.
图1-1 图1-2 图1-3 图1-4
5.(2009广东茂名)图1-2杨伯家小院子的四棵小树刚好在其梯形院子各边的中点上,若在四边形种上小草,则这块草地的形状是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
6.如图1-3,下列条件之一能使是菱形的为( )
① ② ③ ④
A.①③ B.②③ C.③④ D.①②③
7.(2009山东济宁)如图图1-4,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A. B. C. D.
8. 将矩形纸片ABCD按如图1-5所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )
A.1 B.2 C. D.
图1-5 图1-6
9. 如图1-6,在ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
A. B. C.四边形AECD是等腰梯形 D.
10.(2009黑龙江大兴安岭)如图1-7在矩形中,,,平分,过点作于,延长、交于点,下列结论中:①;②;③;④,正确的 ( )
图1-7
A.②③ B.③④ C.①②④ D.②③④
二、填空题(每小题3分,共18分)
11.(2009宁夏)如图1-8,梯形的两条对角线交于点,图中面积相等的三角形共有 对.
图1-8 图1-9 图1-10
12.如图1-9,在等腰梯形ABCD中,AD∥BC,AE∥DC,AB=6cm,则AE= cm. 6
13. (2009黑龙江牡丹江)如图1-10,中,、分别为、边上的点,要使需添加一个条件: .
14.(2009江西)如图1-11,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距则 度.
图1-11 图1-12 图1-13
15. (2009吉林长春)如图1-12,l∥m,矩形ABCD的顶点B在直线m上,则∠α= 度.
16. (2008浙江温州)如图1-13,菱形中,,对角线,则菱形的周长等于 .
三、解答题(共8小题,共72分)
17.(2009年安徽芜湖)如图1-14,在梯形中,,
.
图1-14
求的长.
18.(2009海南)如图1-15所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答
下列问题:
图1-15
(1)分别写出点A、B两点的坐标;
(2)作出△ABC关于坐标原点成中心对称的△A1B1C1;
(3)作出点C关于是x轴的对称点P. 若点P向右平移x个单位长度后落在△A1B1C1的内部,请直接写出x的取值范围.
19.如图1-16,在ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F.
图1-16
(1)求证:△ADE≌△FCE;
(2)连结AC、DF,则四边形ACFD是下列选项中的( ).A.梯形 B.菱形 C.正方形 D.平行四边形
20.如图1-17,在梯形ABCD中,AB∥DC, DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
图1-17
(1)求证:梯形ABCD是等腰梯形.
(2)若∠BDC=30°,AD=5,求CD的长.
21.如图1-18,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC,交BC的延长线于F。
图1-18
请你猜想DE与DF的大小有什么关系?并证明你的猜想
22.如图1-19,在△ABC中,∠A、∠B的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.
(1)点D是△ABC的________心;
(2)求证:四边形DECF为菱形.
23.如图1-20,在梯形中,,,,于点E,F是CD的中点,DG是梯形的高.
图1-20
(1)求证:四边形AEFD是平行四边形;
(2)设,四边形DEGF的面积为y,求y关于x的函数关系式.
24.已知:如图1-21所示的一张矩形纸片(),将纸片折叠一次,使点与重合,再展开,折痕交边于,交边于,分别连结和.
图1-21
(1)求证:四边形是菱形;
(2)若,的面积为,求的周长;
(3)在线段上是否存在一点,使得?若存在,请说明点的位置,并予以证明;若不存在,请说明理由.
第一章 特殊四边形单元检测答案
一、1.B 2.C 3.A 4.B 5.A 6.A 7.C 8.D 9.A 10.D
二、11.3 12.6 13.
14.120 15.25 16.32
三、17.解:作于于
四边形是矩形.
是的边上的中线.
在中,
18.(1)A、B两点的坐标分别为(-1,0)、(-2,-2);
(2)所作△A1B1C1如图所示;
(3)所作点P如上图所示,5.5 < x <8 .
19.证明:(1) ∵ 四边形ABCD是平行四边形,∴ AD∥BF,∴ ∠D=∠ECF.
∵ E是CD的中点,∴ DE = CE.又 ∠AED=∠FEC, ∴ △ADE≌△FCE.
(2) D.或填“平行四边形”.
20.(1)证明:∵AE∥BD, ∴∠E=∠BDC
∵DB平分∠ADC ∴∠ADC=2∠BDC
又∵∠C=2∠E∴∠ADC=∠BCD∴梯形ABCD是等腰梯形
(2)解:由第(1)问,得∠C=2∠E=2∠BDC=60°,且BC=AD=5
∵ 在△BCD中,∠C=60°, ∠BDC=30°∴∠DBC=90°∴DC=2BC=10
21.解:DE=DF
证明如下:连结BD
∵四边形ABCD是菱形 ∴∠CBD=∠ABD(菱形的对角线平分一组对角)
∵DF⊥BC,DE⊥AB ∴DF=DE(角平分线上的点到角两边的距离相等)
22.(1) 内.
(2) 证明:连接CD,
∵ DE∥AC,DF∥BC, ∴ 四边形DECF为平行四边形,
又∵ 点D是△ABC的内心, ∴ CD平分∠ACB,即∠FCD=∠ECD,
又∠FDC=∠ECD,∴ ∠FCD=∠FDC ∴ FC=FD, ∴ □DECF为菱形.
23.(1) 证明: ∵,∴梯形ABCD为等腰梯形.∵∠C=60°,∴,
又∵,∴.∴.∴.
由已知,∴AE∥DC.
又∵AE为等腰三角形ABD的高, ∴E是BD的中点, ∵F是DC的中点, ∴EF∥BC. ∴EF∥AD.
∴四边形AEFD是平行四边形.
(2)解:在Rt△AED中, ,∵,∴.
在Rt△DGC中 ∠C=60°,并且,∴.
由(1)知: 在平行四边形AEFD中,又∵,∴,
∴四边形DEGF的面积,
∴ .
24.解:(1)连结交于,
当顶点与重合时,折痕垂直平分,
,
在平行四边形中,,
,
.
四边形是菱形.
(2)四边形是菱形,.
设,,,
①
又,则. ②
由①、②得:
,(不合题意舍去)
的周长为.
(3)过作交于,则就是所求的点.
证明:由作法,,
由(1)得:,又,
,
,则
四边形是菱形,,.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
