第五章 相交线后七节
图片预览



文档简介
第九课时 5.3.1平行线的性质(1)
一、学习目标:
1、知道两直线平行的性质;
2、会进行简单的书写推理过程,进一步培养逻辑推理能力。
二、重点与难点
重点:知道两直线平行的性质 难点:推理过程的书写
三、铺垫回顾
问题:如何判定两条直线平行呢?
过渡:已知两条直线平行,同位角、内错角、同旁内角各有什么关系?
四、新知探究
1、如图,两条平行直线a与b被直线l所截,动手量一量∠1与∠5、∠3与∠5、
∠4与∠5有什么关系?
猜测结论:两条平行直线被第三条直线所截,同位角 ,内错角 ,同旁内角 。
【思考】如果直线a与b不平行,你的猜想还成立吗?
总结:平行线的性质:
性质一:
性质二:
性质三:
2、你能用两直线平行,同位角相等来说明其他两个结论吗 (如上图)
已知:a∥b, 已知:a∥b,
求证:∠3=∠5 求证:∠5+∠4=180°
解:∵a∥b(已知) 解:∵a∥b(已知)
∴∠ =∠5(两直线平行,同位角相等) ∴∠ =∠5(两直线平行,同位角相等)
又∵∠1=∠ (对顶角相等) 又∵∠1+∠4=180°(邻补角)
∴∠ =∠5(等量代换) ∴∠ + ∠4=180°(等量代换)
3.自学课本20页例题。
【对应练习】
1.课本21页“练习1”
2.课本23页3、4题
五、当堂检测
1.如图所示,已知直线AB、CD被直线EF所截,且AB∥CD,若∠1=50°,则∠2=____,∠3=_____.
(第1题) (第2题) (第3题)
2.如图所示,已知AB∥CD,BC∥DE,∠1=120°,则∠2=______.
3.如图所示,AB∥CD,AF交CD于E,若∠CEF=60°,则∠A=______.
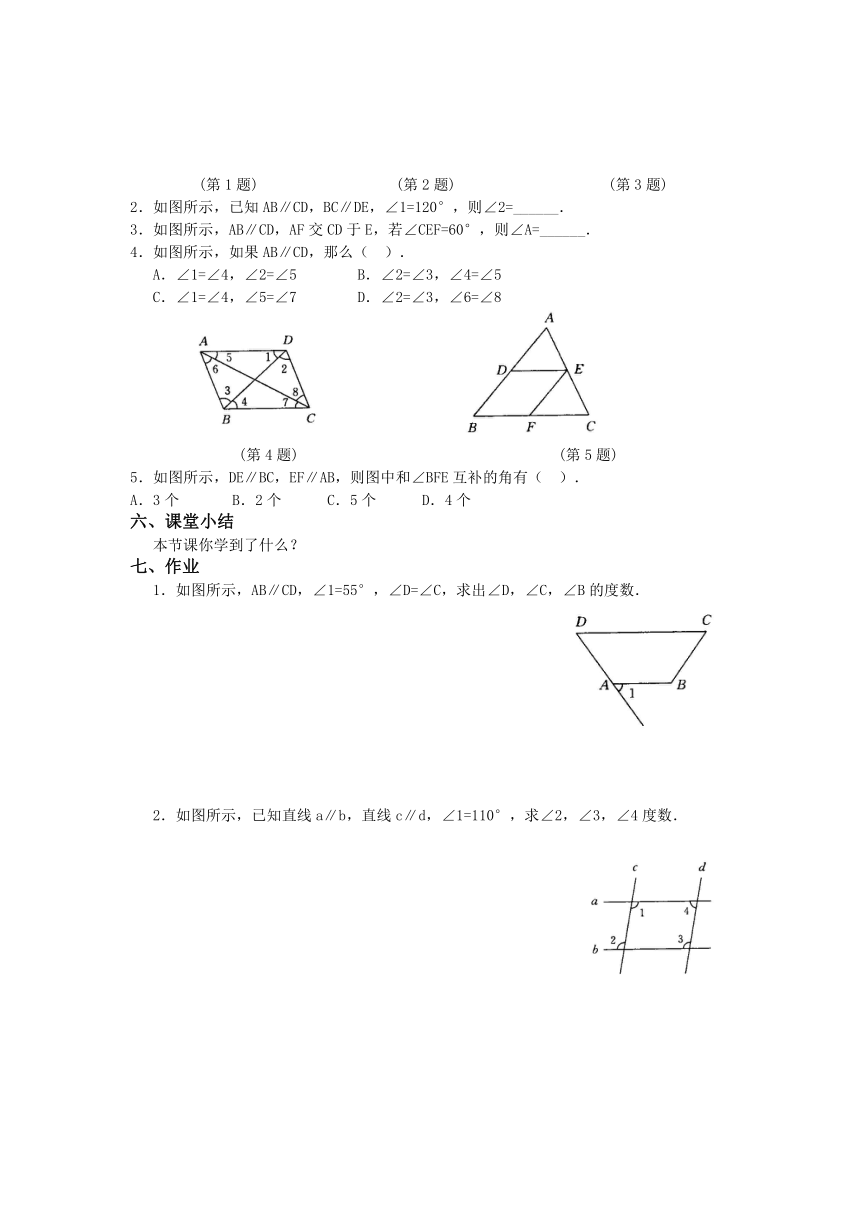
4.如图所示,如果AB∥CD,那么( ).
A.∠1=∠4,∠2=∠5 B.∠2=∠3,∠4=∠5
C.∠1=∠4,∠5=∠7 D.∠2=∠3,∠6=∠8
(第4题) (第5题)
5.如图所示,DE∥BC,EF∥AB,则图中和∠BFE互补的角有( ).
A.3个 B.2个 C.5个 D.4个
六、课堂小结
本节课你学到了什么?
七、作业
1.如图所示,AB∥CD,∠1=55°,∠D=∠C,求出∠D,∠C,∠B的度数.
2.如图所示,已知直线a∥b,直线c∥d,∠1=110°,求∠2,∠3,∠4度数.
第十课时 5.3.1平行线的性质(2)
一、学习目标:
1.知道平行线的判定方法和性质,以及平行线的性质和判定的区别.
2.会用平行线的判定方法和性质进行简单的推理论证.
二、重点与难点:
重点:知道平行线的判定方法和性质 难点:推理论证过程的书写
三、铺垫回顾:
1、平行线的判定:两直线被第三条直线所截
(1)_________,两直线平行。
(2)_________,两直线平行。
(3)_________,两直线平行。
2、平行线的性质:两条平行线被第三条直线所截
(1)两直线平行,_________。
(2)两直线平行,_________。
(3)两直线平行,_________。
3、平行线的判定与性质区分:
由角 线 ,用用平行线的判定;
由线 角 ,用用平行线的性质。
四、当堂检测:
1.如图1,A.B.C三点在一条直线上.
如果∠3 =∠6,那么 ∥ .( )
如果∠6 =∠9,那么 ∥ .( )
*如果∠1 +∠2 +∠3=180°,那么 ∥ .( )
*如果∠ =∠ ,那么BE∥CD.( )
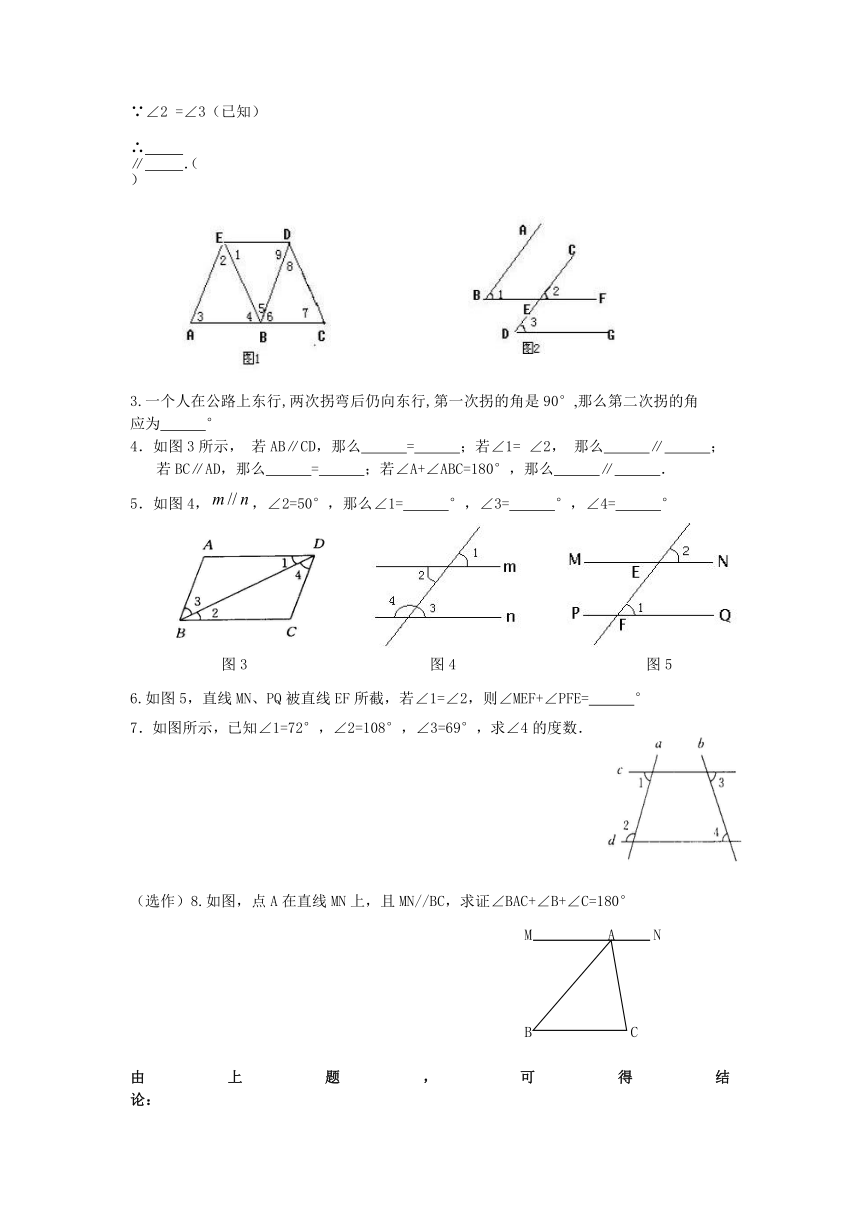
2.如图2,看图填空:
∵∠1 =∠2(已知)
∴ ∥ .( )
∵∠2 =∠3(已知)
∴ ∥ .( )
3.一个人在公路上东行,两次拐弯后仍向东行,第一次拐的角是90°,那么第二次拐的角
应为 °
4.如图3所示, 若AB∥CD,那么 = ;若∠1=∠2,那么 ∥ ;
若BC∥AD,那么 = ;若∠A+∠ABC=180°,那么 ∥ .
5.如图4,,∠2=50°,那么∠1= °,∠3= °,∠4= °
图3 图4 图5
6.如图5,直线MN、PQ被直线EF所截,若∠1=∠2,则∠MEF+∠PFE= °
7.如图所示,已知∠1=72°,∠2=108°,∠3=69°,求∠4的度数.
(选作)8.如图,点A在直线MN上,且MN//BC,求证∠BAC+∠B+∠C=180°
M A N
B C
由上题,可得结论:
五、拓展延伸
1.推理填空:如图,已知AB∥CD,求∠B+∠BED+∠D的度数。
解:过E作EF∥AB, B A
则∠B+∠BEF=1800 ( )
∵AB∥CD( 已知 ) E F
∴EF∥CD( )
∴∠FED+∠D=1800 ( ) D C
∵∠BED=∠FEB+∠FED
∴∠B+∠BED+∠D=3600
*2.变式训练:已知AB∥DE,试说明∠B+∠D=∠BCD.
第十一课时5.3.2 命题、定理
一、学习目标:
1、知道命题、真命题、假命题、定理的含义,会区分命题的题设和结论;
2、能区分命题的题设和结论,会把一些简单命题改写成“如果……那么……”的形式。
二、重点与难点:
重点:知道命题、真命题、假命题、定理的含义,会区分命题的题设和结论
难点:能区分命题的题设和结论,会把一些简单命题改写成“如果……那么……”的形式
三、新知探究:
自学课本21页—22页内容,完成以下问题。
1、对一件事情____ ____的语句,叫做命题。
2、命题由______和________组成。__________是已知事项, __________是由已知事项推出的事项。
3、命题常可以写成__________的形式。“__________”后接的部分是题设,“__________”后面接的部分是结论。如何指出命题的题设和结论?
4、 ________ __叫真命题, ______ ___叫假命题,______ ____叫定理。
5、举例说明定理,例如:如果两个角是对顶角,那么这两个角相等;
其题设是 ,结论是 。
【对应练习】
1、叙述平行线的判定方法与性质,你能分析出这些语句的题设与结论吗?(口答)
2、课本22页练习。
四、当堂检测
1.下列语句是命题的个数为( ).
①画∠AOB的平分线; ②直角都相等; ③同旁内角互补吗? ④若│a│=3,则a=3.
A.1个 B.2个 C.3个 D.4个
2.“同一平面内,垂直于同一条直线的两条直线互相平行”是____命题,改写成“如果……那么……”的形式是______________________ ,
题设是___________ __,结论是 .
3.下列5个命题,其中真命题的个数为( ).
①两个锐角之和一定是钝角; ②直角小于夹角; ③同位角相等,两直线平行;
④内错角互补,两直线平行; ⑤如果aA.1个 B.2个 C.3个 D.4个
4.下列说法正确的是( ).
A.互补的两个角是邻补角; B.两直线平行,同旁内角相等;
C.“同旁内角互补”不是命题; D.“相等的两个角是对顶角”是假命题
5.将下列命题改写成“如果……那么……”的形式,并判断是真命题,还是假命题。若是假命题,请举出一个反例.
(1)邻补角是互补的角。
(2)两个角的和是平角的时候,这两个角互为补角。
(3)内错角相等。
(4)两条平行线被第三条直线所截,同旁内角互补。
(5)若a>b,则ac2>bc2。
五、课堂小结
本节课你学到了哪些知识?
六、作业
1、把下列命题改写成“如果……那么……”的形式,并判断是真命题,还是假命题。若是假命题,举出一个反例。
(1)内错角相等,两直线平行。
(2)等角的余角相等。
(3)同角的余角相等。
(4)在同一平面内,平行于同一条直线的两直线平行。
(5)相等的角是对顶角。
(6)互补的角是邻补角。
第十二课时 5.4平移(1)
一、学习目标:
1、知道平移的概念,会进行图形的平移。
2、知道平移的性质,能解决简单的平移问题。
二、重点与难点:
重点:知道平移的概念,平移的性质 难点:能解决简单的平移问题
三、新知探究:
1.仔细观察课本27页美丽的图案,看它们有什么共同的特点?然后完成27页的探究.(口答)
2.完成28页的思考和以下填空?
(1)在平面内,将一个图形沿某个方向 一定的距离,这样的图形运动称为平移,平移改变的是图形的 。平移不改变图形的 和 。
(2)平移后得到的新图形与原图形的 和 完全相同,只改变了原图形的 ,找准新图形与原图形上的对应点,连接各组对应点的线段 且 。
3、图形的平移是由 和 决定的。
【尝试练习】
1、下列各组图形中,可以经过平移变换由一个图形得到另一个图形的是( )
2.将图形平移,下列结论错误的是( )
A.对应线段相等; B.对应角相等
C.对应点所连的线段互相平分; D.对应点所连的线段相等
四、当堂检测:
1、下列哪个图形是由左图平移得到的( )
2.线段AB沿和它垂直的方向平移到A′B′,则线段AB和线段A′B′的位置关系是______ .
3.小明的一本书一共有104页,在这104页的页码中有两个数码的,并且这两个数 码经过平移其中一个能得到另一个,则这样的页共有________页.
4.如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长 B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长 D.沿射线BD的方向移动DC长
5.将△ABC平移到△DEF,不能确定△DEF位置的是( )
A.已知平移的方向 B.已知点A的对应点D的位置
C.已知边AB的对应边DE的位置 D.已知∠A的对应角∠D的位置
6.如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
A、 AB∥DE且AB=DE B、 ∠DEC=∠B
C、 AD∥EC且AD=EC D、 BC=AD+EC
7.△ABC沿BC的方向平移到△DEF的位置,
(1)若∠B=260,∠F=740,则∠1=___,∠2=____,∠A=___,∠D=___
(2)若AB=4cm,AC=5cm,BC=4.5cm,EC=3.5cm,则平移的距离等于_____, DF=_____,CF=____。
(选做)1.直角△ABC中,∠C=900,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为 cm2。
2.如图所示的是用火柴杆摆的一只向左飞行的小鸟,你能只平移3根火柴杆就 使它向右飞吗
五、课堂小结
本节课你学到了哪些知识?
六、作业
1、如图1所示,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( )
A、△OCD B、△OAB C、△OAF D、△OEF
2.如图2所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分 别是( )
A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC
(图1) (图2)
第十三课时5.4 平移(2)
一、学习目标:
1、依据图形平移的性质,按要求能作出简单的平面图形平移后的图形,总结作法。
2、分析平移变换图案,会进行简单的图案设计,发展空间观念。
二、重点与难点:
重点与难点:能作出简单的平面图形平移后的图形
三、铺垫回顾:
1、什么是图形的平移?平移具有哪些性质?(口答)
思考:你能运用平移的性质按要求平移一个图形吗?
三、新知探究
如图,平移三角形ABC,使点A运动到A′,画出平移后的
三角形A′B′C′
(1)点A平移后的对应点是 ,你能在图上画出点A平移的方向吗?
点A移动的距离就是线段 的长度。
(2)点B平移的方向应与点A平移的方向 ,距离 。
你能画出B′的位置吗?点C的对应点C′呢?
(3)请连接出三角形A′B′C′.
总结作图步骤:1 找(关键点),2移(作平行线),3连(画)。
【尝试练习】
1、如图,有一条小船,若把小船平移,使点A平移到点B,请你在图中画出平移后的小船。
四、当堂检测:
1.如图,△DEF是把△ABC沿水平方向向右平移4厘米得到的,请你作出△ABC.
2.经过平移,△ABC的边AB平移到了A′B′,作出平移后的三角形,你能给出几种作法?你认为哪种方法更简便?请用其中一种方法作出平移后的三角形.
五、课堂小结:
本节课你学到了哪些知识?
六、作业:
1、如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对 应点D、点C的对应点F的位置.
2、如图,在方纸中平移△ABC,使点A移到点M,画出平移后的△MNP.
第十四课时 单元小结
知识梳理:
知识点一:能找出图形中某个角的邻补角和对顶角,并能用对顶角相等的性质计算角度.
【对应练习】
1.如图1,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF 的邻补角是_____ ___,∠AOE的对顶角是_______,∠AOF 的邻补角是___ _,∠AOC 的邻补角是 。
图1 图2 图3
2.如图2,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠BOD=____,∠COB=____,∠EOF=____.
知识点二:1.能说出垂线的性质“经过一点,能画出已知直线的一条垂线,并且只能画出一条垂线”。
2.会用三角尺或量角器过一点画一条直线的垂线。3.知道垂线段的概念,点到直线的距离的意义。
【对应练习】
1.垂线的性质:过一点有且只有_______与已知直线_______.
2如图3,分别过P画AB的垂线.
3.连结直线外一点与直线上各点的所有线段中,________最短.
4.直线外一点到这条直线的________的长度,叫做点到直线的距离. 图4
5.如图4,若∠ACB=90°,BC=8cm,AC=6cm,则B点到AC边的距离为__ ___,A点到BC边
的距离为________.
知识点三:会识别图形(包括变式图形和复杂图形)中的同位角、内错角和同旁内角。
【对应练习】
1.如图5,图中的同位角有______对.
2.如图6,∠1与∠2是哪两条直线被哪一条直线所截,构成的是什么角的关系?∠3与∠4,∠3
与∠D呢?
图5 图6
知识点四:
1.知道平行线的概念,能说出平面内两条直线的位置关系。
2.能说出平行公理以及平行公理的推论。
3.知道平行线判定公理和判定定理,并能用判定公理及判定定理进行简单的推理论证.
4.知道两直线平行的性质,会进行简单的书写推理过程。
5.会用平行线的判定方法和性质进行简单的推理论证.
【对应练习】
1.设a,b,c为平面内三条不同直线:(1)若a∥b,b∥c,则a与c的位置关系是______;
(2)若a∥b,c⊥a,则b与c的位置关系是______。
2.如图所示,能说明AB∥DE的有( )
①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
*3.如图所示,能使AD∥BC的条件是( )
A.∠2=∠3 B.∠1=∠4
C.∠1+∠2=∠3+∠4 D.∠A+∠C=180°
4.如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?
解:因为∠1+∠2=180°( )
所以AB∥_______( )
又因为∠1=∠3( )
所以∠2+∠________=180°( )
所以EF∥GH(同旁内角互补,两直线平行)
知识点五:
1.知道命题、真命题、假命题、定理的含义,会区分命题的题设和结论;
2.知道平移的概念,会进行图形的平移,并能根据平移的性质解决简单的平移问题。
【对应练习】
1.把命题“对顶角相等”写成“如果……那么……”的形式为_____ ____.
2. 已知三角形ABC,点A的对应点是点D,作出三角形ABC平移后的图形。
第十五课时 练习
一、选择题.
1.在下列图中,∠1与∠2属于对顶角的是( ).
2.下列说法不正确的是( ).
A.同位角相等,两直线平行; B.两直线平行,内错角相等
C.内错角相等,两直线平行; D.同旁内角互余,两直线平行
(第3题) (第4题) (第5题)
3.如图所示,在下列条件中,不能判定直线L1∥L2的是( ).
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
4.如图是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°,则∠C的度数为( ).
A.120° B.100° C.140° D.90°
5.如图所示,在△ABC中,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只要满足( ). A.∠1=∠2 B.∠1=∠DFE; C.∠1=∠AFD D.∠2=∠AFD
6.下列说法错误的是( ).
A.平移不改变图形的形状
B.图形经过平移,新图形与原图形中的对应线段、对应角分别相等
C.图形平移后,连结各组对应点的线段平行(或在一条直线上)且相等
D.平移可能改变图形的大小
二、填空题
7.如图所示,直线a和b相交于点O,若∠1=50°,则∠2=____,∠3=______.
(第7题) (第8题) (第9题)
8.如图所示,计划把河中的水引到水池C中,可过C作CD⊥AB,垂足为D,然后沿CD开渠,则能使所开渠最短,这样设计的依据是________.
9.如图所示,已知点O在直线AB上,OC和OD是射线,若∠1=30°,∠2=60°,那么OC和OD的位置关系是________.
10.如图所示,在△ABC中,∠B=90°,BC=6,AB=8,AC=10,则点B到AC的距离是_______.
(第10题) (第11题) (第12题) (第15题)
11.如图所示,已知∠1=60°,∠2=120°,∠3=70°,则∠4=________.
12、如图,一张宽度相等的纸条,折叠后,若∠ABC=110°,则∠1的度数为_________。
13.两条平行线被第三条直线所截,一组同旁内角的平分线的位置关系是互相______.
14.把命题“等角的补角相等”写成“如果……那么……”的形式是:______________________________________ .
15.如图所示,△ABC平移得到△DEF,已知∠B=45°,∠C=65°,AB=2cm,则∠DFE=____,DE=____.
三、解答题:
16.如图,已知,,,求和的度数。
17.如图所示,已知AB∥DC,∠BAD=∠DCB,说明AD∥BC.
18.如图,∠1=∠2,∠D=∠A,那么∠B=∠C吗 为什么
一、学习目标:
1、知道两直线平行的性质;
2、会进行简单的书写推理过程,进一步培养逻辑推理能力。
二、重点与难点
重点:知道两直线平行的性质 难点:推理过程的书写
三、铺垫回顾
问题:如何判定两条直线平行呢?
过渡:已知两条直线平行,同位角、内错角、同旁内角各有什么关系?
四、新知探究
1、如图,两条平行直线a与b被直线l所截,动手量一量∠1与∠5、∠3与∠5、
∠4与∠5有什么关系?
猜测结论:两条平行直线被第三条直线所截,同位角 ,内错角 ,同旁内角 。
【思考】如果直线a与b不平行,你的猜想还成立吗?
总结:平行线的性质:
性质一:
性质二:
性质三:
2、你能用两直线平行,同位角相等来说明其他两个结论吗 (如上图)
已知:a∥b, 已知:a∥b,
求证:∠3=∠5 求证:∠5+∠4=180°
解:∵a∥b(已知) 解:∵a∥b(已知)
∴∠ =∠5(两直线平行,同位角相等) ∴∠ =∠5(两直线平行,同位角相等)
又∵∠1=∠ (对顶角相等) 又∵∠1+∠4=180°(邻补角)
∴∠ =∠5(等量代换) ∴∠ + ∠4=180°(等量代换)
3.自学课本20页例题。
【对应练习】
1.课本21页“练习1”
2.课本23页3、4题
五、当堂检测
1.如图所示,已知直线AB、CD被直线EF所截,且AB∥CD,若∠1=50°,则∠2=____,∠3=_____.
(第1题) (第2题) (第3题)
2.如图所示,已知AB∥CD,BC∥DE,∠1=120°,则∠2=______.
3.如图所示,AB∥CD,AF交CD于E,若∠CEF=60°,则∠A=______.
4.如图所示,如果AB∥CD,那么( ).
A.∠1=∠4,∠2=∠5 B.∠2=∠3,∠4=∠5
C.∠1=∠4,∠5=∠7 D.∠2=∠3,∠6=∠8
(第4题) (第5题)
5.如图所示,DE∥BC,EF∥AB,则图中和∠BFE互补的角有( ).
A.3个 B.2个 C.5个 D.4个
六、课堂小结
本节课你学到了什么?
七、作业
1.如图所示,AB∥CD,∠1=55°,∠D=∠C,求出∠D,∠C,∠B的度数.
2.如图所示,已知直线a∥b,直线c∥d,∠1=110°,求∠2,∠3,∠4度数.
第十课时 5.3.1平行线的性质(2)
一、学习目标:
1.知道平行线的判定方法和性质,以及平行线的性质和判定的区别.
2.会用平行线的判定方法和性质进行简单的推理论证.
二、重点与难点:
重点:知道平行线的判定方法和性质 难点:推理论证过程的书写
三、铺垫回顾:
1、平行线的判定:两直线被第三条直线所截
(1)_________,两直线平行。
(2)_________,两直线平行。
(3)_________,两直线平行。
2、平行线的性质:两条平行线被第三条直线所截
(1)两直线平行,_________。
(2)两直线平行,_________。
(3)两直线平行,_________。
3、平行线的判定与性质区分:
由角 线 ,用用平行线的判定;
由线 角 ,用用平行线的性质。
四、当堂检测:
1.如图1,A.B.C三点在一条直线上.
如果∠3 =∠6,那么 ∥ .( )
如果∠6 =∠9,那么 ∥ .( )
*如果∠1 +∠2 +∠3=180°,那么 ∥ .( )
*如果∠ =∠ ,那么BE∥CD.( )
2.如图2,看图填空:
∵∠1 =∠2(已知)
∴ ∥ .( )
∵∠2 =∠3(已知)
∴ ∥ .( )
3.一个人在公路上东行,两次拐弯后仍向东行,第一次拐的角是90°,那么第二次拐的角
应为 °
4.如图3所示, 若AB∥CD,那么 = ;若∠1=∠2,那么 ∥ ;
若BC∥AD,那么 = ;若∠A+∠ABC=180°,那么 ∥ .
5.如图4,,∠2=50°,那么∠1= °,∠3= °,∠4= °
图3 图4 图5
6.如图5,直线MN、PQ被直线EF所截,若∠1=∠2,则∠MEF+∠PFE= °
7.如图所示,已知∠1=72°,∠2=108°,∠3=69°,求∠4的度数.
(选作)8.如图,点A在直线MN上,且MN//BC,求证∠BAC+∠B+∠C=180°
M A N
B C
由上题,可得结论:
五、拓展延伸
1.推理填空:如图,已知AB∥CD,求∠B+∠BED+∠D的度数。
解:过E作EF∥AB, B A
则∠B+∠BEF=1800 ( )
∵AB∥CD( 已知 ) E F
∴EF∥CD( )
∴∠FED+∠D=1800 ( ) D C
∵∠BED=∠FEB+∠FED
∴∠B+∠BED+∠D=3600
*2.变式训练:已知AB∥DE,试说明∠B+∠D=∠BCD.
第十一课时5.3.2 命题、定理
一、学习目标:
1、知道命题、真命题、假命题、定理的含义,会区分命题的题设和结论;
2、能区分命题的题设和结论,会把一些简单命题改写成“如果……那么……”的形式。
二、重点与难点:
重点:知道命题、真命题、假命题、定理的含义,会区分命题的题设和结论
难点:能区分命题的题设和结论,会把一些简单命题改写成“如果……那么……”的形式
三、新知探究:
自学课本21页—22页内容,完成以下问题。
1、对一件事情____ ____的语句,叫做命题。
2、命题由______和________组成。__________是已知事项, __________是由已知事项推出的事项。
3、命题常可以写成__________的形式。“__________”后接的部分是题设,“__________”后面接的部分是结论。如何指出命题的题设和结论?
4、 ________ __叫真命题, ______ ___叫假命题,______ ____叫定理。
5、举例说明定理,例如:如果两个角是对顶角,那么这两个角相等;
其题设是 ,结论是 。
【对应练习】
1、叙述平行线的判定方法与性质,你能分析出这些语句的题设与结论吗?(口答)
2、课本22页练习。
四、当堂检测
1.下列语句是命题的个数为( ).
①画∠AOB的平分线; ②直角都相等; ③同旁内角互补吗? ④若│a│=3,则a=3.
A.1个 B.2个 C.3个 D.4个
2.“同一平面内,垂直于同一条直线的两条直线互相平行”是____命题,改写成“如果……那么……”的形式是______________________ ,
题设是___________ __,结论是 .
3.下列5个命题,其中真命题的个数为( ).
①两个锐角之和一定是钝角; ②直角小于夹角; ③同位角相等,两直线平行;
④内错角互补,两直线平行; ⑤如果a
4.下列说法正确的是( ).
A.互补的两个角是邻补角; B.两直线平行,同旁内角相等;
C.“同旁内角互补”不是命题; D.“相等的两个角是对顶角”是假命题
5.将下列命题改写成“如果……那么……”的形式,并判断是真命题,还是假命题。若是假命题,请举出一个反例.
(1)邻补角是互补的角。
(2)两个角的和是平角的时候,这两个角互为补角。
(3)内错角相等。
(4)两条平行线被第三条直线所截,同旁内角互补。
(5)若a>b,则ac2>bc2。
五、课堂小结
本节课你学到了哪些知识?
六、作业
1、把下列命题改写成“如果……那么……”的形式,并判断是真命题,还是假命题。若是假命题,举出一个反例。
(1)内错角相等,两直线平行。
(2)等角的余角相等。
(3)同角的余角相等。
(4)在同一平面内,平行于同一条直线的两直线平行。
(5)相等的角是对顶角。
(6)互补的角是邻补角。
第十二课时 5.4平移(1)
一、学习目标:
1、知道平移的概念,会进行图形的平移。
2、知道平移的性质,能解决简单的平移问题。
二、重点与难点:
重点:知道平移的概念,平移的性质 难点:能解决简单的平移问题
三、新知探究:
1.仔细观察课本27页美丽的图案,看它们有什么共同的特点?然后完成27页的探究.(口答)
2.完成28页的思考和以下填空?
(1)在平面内,将一个图形沿某个方向 一定的距离,这样的图形运动称为平移,平移改变的是图形的 。平移不改变图形的 和 。
(2)平移后得到的新图形与原图形的 和 完全相同,只改变了原图形的 ,找准新图形与原图形上的对应点,连接各组对应点的线段 且 。
3、图形的平移是由 和 决定的。
【尝试练习】
1、下列各组图形中,可以经过平移变换由一个图形得到另一个图形的是( )
2.将图形平移,下列结论错误的是( )
A.对应线段相等; B.对应角相等
C.对应点所连的线段互相平分; D.对应点所连的线段相等
四、当堂检测:
1、下列哪个图形是由左图平移得到的( )
2.线段AB沿和它垂直的方向平移到A′B′,则线段AB和线段A′B′的位置关系是______ .
3.小明的一本书一共有104页,在这104页的页码中有两个数码的,并且这两个数 码经过平移其中一个能得到另一个,则这样的页共有________页.
4.如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长 B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长 D.沿射线BD的方向移动DC长
5.将△ABC平移到△DEF,不能确定△DEF位置的是( )
A.已知平移的方向 B.已知点A的对应点D的位置
C.已知边AB的对应边DE的位置 D.已知∠A的对应角∠D的位置
6.如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
A、 AB∥DE且AB=DE B、 ∠DEC=∠B
C、 AD∥EC且AD=EC D、 BC=AD+EC
7.△ABC沿BC的方向平移到△DEF的位置,
(1)若∠B=260,∠F=740,则∠1=___,∠2=____,∠A=___,∠D=___
(2)若AB=4cm,AC=5cm,BC=4.5cm,EC=3.5cm,则平移的距离等于_____, DF=_____,CF=____。
(选做)1.直角△ABC中,∠C=900,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为 cm2。
2.如图所示的是用火柴杆摆的一只向左飞行的小鸟,你能只平移3根火柴杆就 使它向右飞吗
五、课堂小结
本节课你学到了哪些知识?
六、作业
1、如图1所示,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( )
A、△OCD B、△OAB C、△OAF D、△OEF
2.如图2所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分 别是( )
A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC
(图1) (图2)
第十三课时5.4 平移(2)
一、学习目标:
1、依据图形平移的性质,按要求能作出简单的平面图形平移后的图形,总结作法。
2、分析平移变换图案,会进行简单的图案设计,发展空间观念。
二、重点与难点:
重点与难点:能作出简单的平面图形平移后的图形
三、铺垫回顾:
1、什么是图形的平移?平移具有哪些性质?(口答)
思考:你能运用平移的性质按要求平移一个图形吗?
三、新知探究
如图,平移三角形ABC,使点A运动到A′,画出平移后的
三角形A′B′C′
(1)点A平移后的对应点是 ,你能在图上画出点A平移的方向吗?
点A移动的距离就是线段 的长度。
(2)点B平移的方向应与点A平移的方向 ,距离 。
你能画出B′的位置吗?点C的对应点C′呢?
(3)请连接出三角形A′B′C′.
总结作图步骤:1 找(关键点),2移(作平行线),3连(画)。
【尝试练习】
1、如图,有一条小船,若把小船平移,使点A平移到点B,请你在图中画出平移后的小船。
四、当堂检测:
1.如图,△DEF是把△ABC沿水平方向向右平移4厘米得到的,请你作出△ABC.
2.经过平移,△ABC的边AB平移到了A′B′,作出平移后的三角形,你能给出几种作法?你认为哪种方法更简便?请用其中一种方法作出平移后的三角形.
五、课堂小结:
本节课你学到了哪些知识?
六、作业:
1、如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对 应点D、点C的对应点F的位置.
2、如图,在方纸中平移△ABC,使点A移到点M,画出平移后的△MNP.
第十四课时 单元小结
知识梳理:
知识点一:能找出图形中某个角的邻补角和对顶角,并能用对顶角相等的性质计算角度.
【对应练习】
1.如图1,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF 的邻补角是_____ ___,∠AOE的对顶角是_______,∠AOF 的邻补角是___ _,∠AOC 的邻补角是 。
图1 图2 图3
2.如图2,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠BOD=____,∠COB=____,∠EOF=____.
知识点二:1.能说出垂线的性质“经过一点,能画出已知直线的一条垂线,并且只能画出一条垂线”。
2.会用三角尺或量角器过一点画一条直线的垂线。3.知道垂线段的概念,点到直线的距离的意义。
【对应练习】
1.垂线的性质:过一点有且只有_______与已知直线_______.
2如图3,分别过P画AB的垂线.
3.连结直线外一点与直线上各点的所有线段中,________最短.
4.直线外一点到这条直线的________的长度,叫做点到直线的距离. 图4
5.如图4,若∠ACB=90°,BC=8cm,AC=6cm,则B点到AC边的距离为__ ___,A点到BC边
的距离为________.
知识点三:会识别图形(包括变式图形和复杂图形)中的同位角、内错角和同旁内角。
【对应练习】
1.如图5,图中的同位角有______对.
2.如图6,∠1与∠2是哪两条直线被哪一条直线所截,构成的是什么角的关系?∠3与∠4,∠3
与∠D呢?
图5 图6
知识点四:
1.知道平行线的概念,能说出平面内两条直线的位置关系。
2.能说出平行公理以及平行公理的推论。
3.知道平行线判定公理和判定定理,并能用判定公理及判定定理进行简单的推理论证.
4.知道两直线平行的性质,会进行简单的书写推理过程。
5.会用平行线的判定方法和性质进行简单的推理论证.
【对应练习】
1.设a,b,c为平面内三条不同直线:(1)若a∥b,b∥c,则a与c的位置关系是______;
(2)若a∥b,c⊥a,则b与c的位置关系是______。
2.如图所示,能说明AB∥DE的有( )
①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
*3.如图所示,能使AD∥BC的条件是( )
A.∠2=∠3 B.∠1=∠4
C.∠1+∠2=∠3+∠4 D.∠A+∠C=180°
4.如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?
解:因为∠1+∠2=180°( )
所以AB∥_______( )
又因为∠1=∠3( )
所以∠2+∠________=180°( )
所以EF∥GH(同旁内角互补,两直线平行)
知识点五:
1.知道命题、真命题、假命题、定理的含义,会区分命题的题设和结论;
2.知道平移的概念,会进行图形的平移,并能根据平移的性质解决简单的平移问题。
【对应练习】
1.把命题“对顶角相等”写成“如果……那么……”的形式为_____ ____.
2. 已知三角形ABC,点A的对应点是点D,作出三角形ABC平移后的图形。
第十五课时 练习
一、选择题.
1.在下列图中,∠1与∠2属于对顶角的是( ).
2.下列说法不正确的是( ).
A.同位角相等,两直线平行; B.两直线平行,内错角相等
C.内错角相等,两直线平行; D.同旁内角互余,两直线平行
(第3题) (第4题) (第5题)
3.如图所示,在下列条件中,不能判定直线L1∥L2的是( ).
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
4.如图是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°,则∠C的度数为( ).
A.120° B.100° C.140° D.90°
5.如图所示,在△ABC中,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只要满足( ). A.∠1=∠2 B.∠1=∠DFE; C.∠1=∠AFD D.∠2=∠AFD
6.下列说法错误的是( ).
A.平移不改变图形的形状
B.图形经过平移,新图形与原图形中的对应线段、对应角分别相等
C.图形平移后,连结各组对应点的线段平行(或在一条直线上)且相等
D.平移可能改变图形的大小
二、填空题
7.如图所示,直线a和b相交于点O,若∠1=50°,则∠2=____,∠3=______.
(第7题) (第8题) (第9题)
8.如图所示,计划把河中的水引到水池C中,可过C作CD⊥AB,垂足为D,然后沿CD开渠,则能使所开渠最短,这样设计的依据是________.
9.如图所示,已知点O在直线AB上,OC和OD是射线,若∠1=30°,∠2=60°,那么OC和OD的位置关系是________.
10.如图所示,在△ABC中,∠B=90°,BC=6,AB=8,AC=10,则点B到AC的距离是_______.
(第10题) (第11题) (第12题) (第15题)
11.如图所示,已知∠1=60°,∠2=120°,∠3=70°,则∠4=________.
12、如图,一张宽度相等的纸条,折叠后,若∠ABC=110°,则∠1的度数为_________。
13.两条平行线被第三条直线所截,一组同旁内角的平分线的位置关系是互相______.
14.把命题“等角的补角相等”写成“如果……那么……”的形式是:______________________________________ .
15.如图所示,△ABC平移得到△DEF,已知∠B=45°,∠C=65°,AB=2cm,则∠DFE=____,DE=____.
三、解答题:
16.如图,已知,,,求和的度数。
17.如图所示,已知AB∥DC,∠BAD=∠DCB,说明AD∥BC.
18.如图,∠1=∠2,∠D=∠A,那么∠B=∠C吗 为什么
