二年级上册数学课件-6.7 整理与提高(数学广场-幻方) 沪教版 (共35张PPT)
文档属性
| 名称 | 二年级上册数学课件-6.7 整理与提高(数学广场-幻方) 沪教版 (共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 20:24:30 | ||
图片预览







文档简介
洛书
洛书
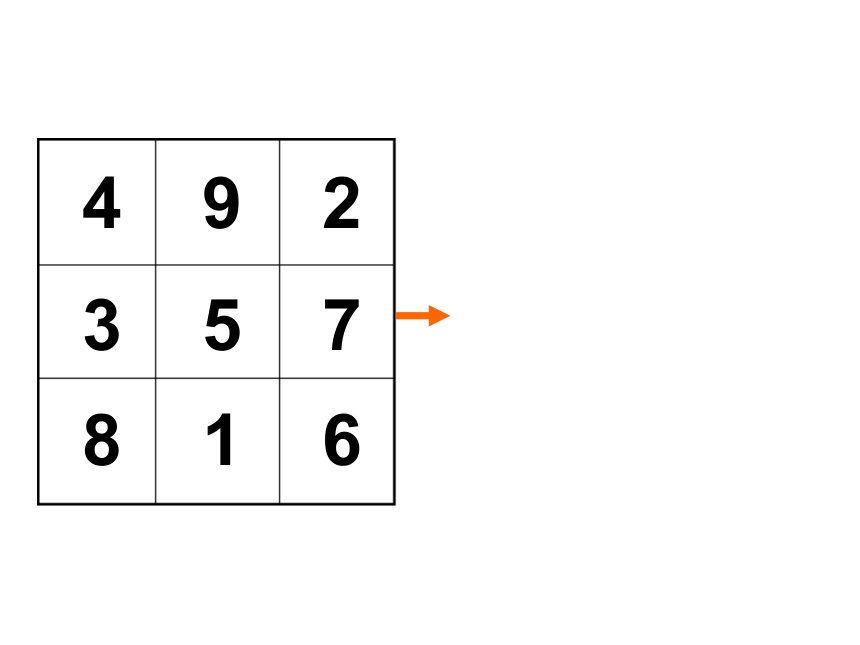
九宫格
4
9
2
3
5
7
8
1
6
1
2
3
4
5
6
7
8
9
5
1
9
3
7
2
4
8
6
2
8
4
6
2
9
4
6
1
8
7
5
3
2
9
4
6
1
8
7
5
3
2
9
4
6
1
8
7
5
3
9
1
2
6
7
5
4
8
3
2
9
4
6
1
8
7
5
3
2
9
4
6
1
8
7
5
3
4
3
8
2
7
6
9
5
1
8
1
6
4
9
2
3
5
7
4
2
3
1
5
9
6
7
8
4
2
3
1
5
9
6
7
8
将两端头的数交换就可成为幻方!
3
5
10
4
6
8
9
2
7
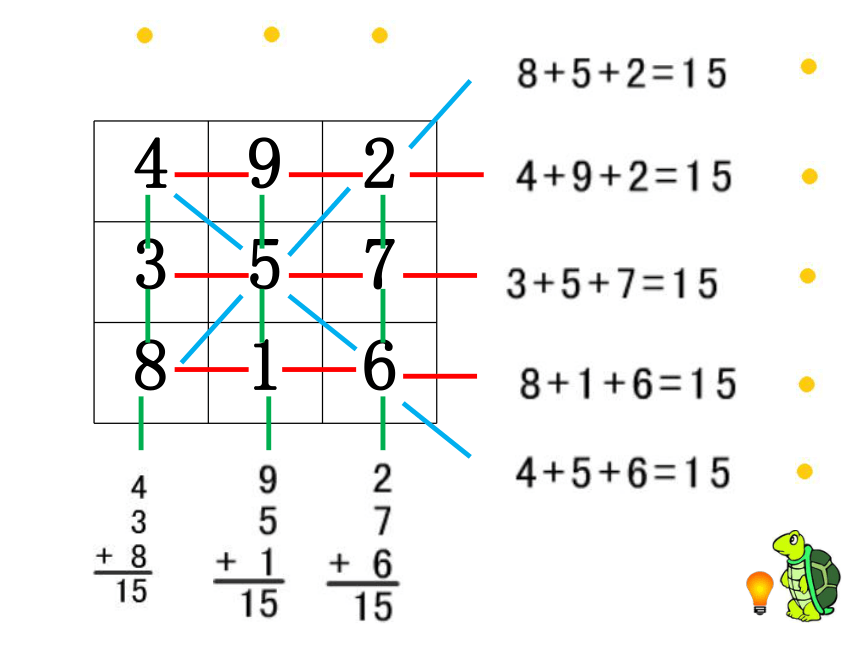
行 列 对角线数字的和相等
所以它是幻方!
4
9
2
3
5
7
8
1
6
3
8
1
7
0
5
2
4
6
( )
√
和是12
2
3
5
9
4
7
8
1
6
( )
×
6
11
4
10
3
8
5
7
9
( )
√
和是21
6
11
4
10
3
8
5
7
9
5
10
3
9
2
7
4
6
8
3
8
1
7
0
5
2
4
6
和是21
和是18
和是12
21=7×3
18=6×3
12=4×3
5
2
1
和是15
3
8
6
和是12
3
5
2
1
3
7
15-5-3=7
8
15-5-2=8
9
15-5-1=9
7
8
9
4
6
和是15
7
0
5
3
8
1
2
4
6
和是12
7
0
5
1
2
4
7
2
9
3
10
5
8
6
4
和是( )
18
(0、1、2、3、4、5、6、7、8)
2
9
4
6
1
8
7
5
3
4
和是15
和是( )
12
3
8
1
5
0
7
2
6
奇妙的幻方世界
*南宋杨辉——研究幻方第一人——1275年
*欧洲的幻方热和名画“忧伤”中的幻方
——1514年
*幻方与外星人——1977年
*出土文物中的阿拉伯幻方——1273年
*美丽的幻方欣赏
中国研究幻方的第一人,数学家——杨辉(南宋)
九子斜排、上下对易
左右向更、四维挺出
戴九履一、左三右七
二四为肩、六八为足
三阶幻方的生成法和布局归结为八句话:
0
1
2
3
4
5
6
7
8
九子斜排
上下对易
左右相更
四维挺出
安西王府遗址中出土的阿拉伯幻方
六阶幻方
历史上另一个著名的
幻方是德国画家、雕刻家
兼数学家Albrecht Duerer
在他著名的雕刻作品《忧
郁者》中创造的。这幅作
品反映了智者的忧郁。画中除了一些几何形体外,还有一个四阶幻方,幻方最后一行中间两个数是15,14,恰好隐含了作画的年代。
丢勒名画 : 忧郁者
有趣的幻方
“完美幻方”
“完美幻方”
九九太极完美幻圆
九九太极完美幻圆
中国的“龟纹聚六图”
国外的“完美六角幻方”
洛书
九宫格
4
9
2
3
5
7
8
1
6
1
2
3
4
5
6
7
8
9
5
1
9
3
7
2
4
8
6
2
8
4
6
2
9
4
6
1
8
7
5
3
2
9
4
6
1
8
7
5
3
2
9
4
6
1
8
7
5
3
9
1
2
6
7
5
4
8
3
2
9
4
6
1
8
7
5
3
2
9
4
6
1
8
7
5
3
4
3
8
2
7
6
9
5
1
8
1
6
4
9
2
3
5
7
4
2
3
1
5
9
6
7
8
4
2
3
1
5
9
6
7
8
将两端头的数交换就可成为幻方!
3
5
10
4
6
8
9
2
7
行 列 对角线数字的和相等
所以它是幻方!
4
9
2
3
5
7
8
1
6
3
8
1
7
0
5
2
4
6
( )
√
和是12
2
3
5
9
4
7
8
1
6
( )
×
6
11
4
10
3
8
5
7
9
( )
√
和是21
6
11
4
10
3
8
5
7
9
5
10
3
9
2
7
4
6
8
3
8
1
7
0
5
2
4
6
和是21
和是18
和是12
21=7×3
18=6×3
12=4×3
5
2
1
和是15
3
8
6
和是12
3
5
2
1
3
7
15-5-3=7
8
15-5-2=8
9
15-5-1=9
7
8
9
4
6
和是15
7
0
5
3
8
1
2
4
6
和是12
7
0
5
1
2
4
7
2
9
3
10
5
8
6
4
和是( )
18
(0、1、2、3、4、5、6、7、8)
2
9
4
6
1
8
7
5
3
4
和是15
和是( )
12
3
8
1
5
0
7
2
6
奇妙的幻方世界
*南宋杨辉——研究幻方第一人——1275年
*欧洲的幻方热和名画“忧伤”中的幻方
——1514年
*幻方与外星人——1977年
*出土文物中的阿拉伯幻方——1273年
*美丽的幻方欣赏
中国研究幻方的第一人,数学家——杨辉(南宋)
九子斜排、上下对易
左右向更、四维挺出
戴九履一、左三右七
二四为肩、六八为足
三阶幻方的生成法和布局归结为八句话:
0
1
2
3
4
5
6
7
8
九子斜排
上下对易
左右相更
四维挺出
安西王府遗址中出土的阿拉伯幻方
六阶幻方
历史上另一个著名的
幻方是德国画家、雕刻家
兼数学家Albrecht Duerer
在他著名的雕刻作品《忧
郁者》中创造的。这幅作
品反映了智者的忧郁。画中除了一些几何形体外,还有一个四阶幻方,幻方最后一行中间两个数是15,14,恰好隐含了作画的年代。
丢勒名画 : 忧郁者
有趣的幻方
“完美幻方”
“完美幻方”
九九太极完美幻圆
九九太极完美幻圆
中国的“龟纹聚六图”
国外的“完美六角幻方”
同课章节目录
- 一、复习与提高
- 两位数加减法的复习
- 加与减
- 巧算
- 方框里填几
- 二、乘法、除法(一)
- 乘法引入
- 看图写乘法算式
- 倍
- 10的乘法
- 5的乘法
- 2的乘法
- 4的乘法
- 8的乘法
- 2、4、8的乘法之间的关系
- 分一分与除法
- 用乘法口诀求商
- 几倍
- 被除数为0的除法
- 小练习(一)
- 三、统计
- 统计表初步
- 条形统计图(一)
- 四、乘法、除法(二)
- 7的乘、除法
- 3的乘、除法
- 6的乘、除法
- 9的乘、除法
- 3、6、9的乘法之间的关系
- “九九”——乘法口诀表
- 看图编乘、除法问题
- 分拆为乘与加
- 有余数的除法
- 有余数除法的计算
- 小练习(二)
- 五、几何小实践
- 角与直角
- 正方体、长方体的初步认识
- 长方形、长方形的初步认识
- 六、整理与提高
- 大家来做乘法
- 乘除大游戏
- 5个3加3个3等于8个3
- 5个3减3个3等于2个3
- 乘与除
- 数学广场——点图与数
- 数学广场——幻方
- 数学广场——从不同方向观察物体
