2020秋苏科版八年级数学上册课件:3.3 勾股定理的简单应用(共15张PPT)
文档属性
| 名称 | 2020秋苏科版八年级数学上册课件:3.3 勾股定理的简单应用(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 12:11:46 | ||
图片预览





文档简介
(共15张PPT)
3.3
勾股定理的简单应用
第3章
勾股定理
课程讲授
新知导入
随堂练习
课堂小结
知识要点
勾股定理的简单应用
新知导入
看一看:
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形。
新知导入
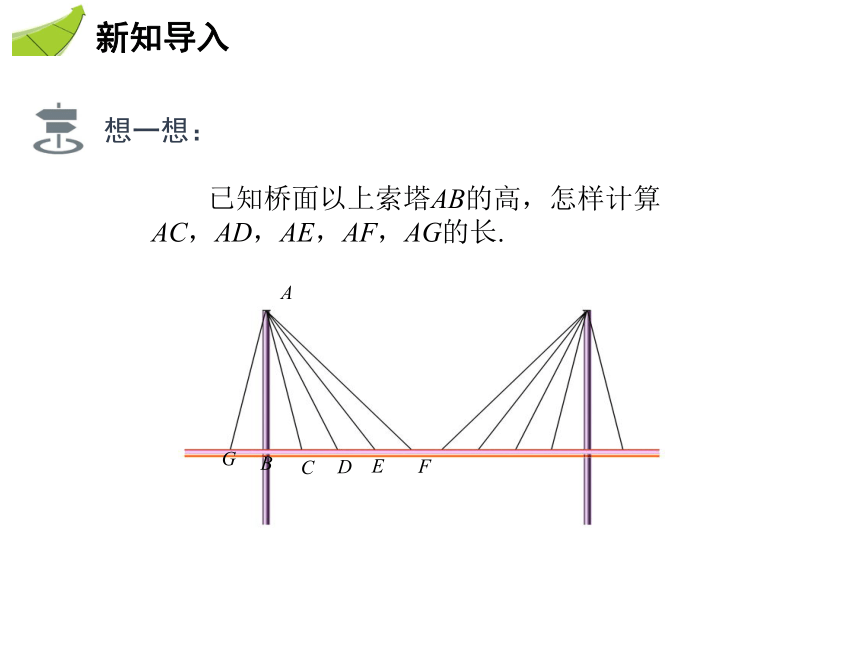
想一想:
已知桥面以上索塔AB的高,怎样计算AC,AD,AE,AF,AG的长.
A
B
C
E
F
G
D
课程讲授
1
勾股定理的简单应用
例1
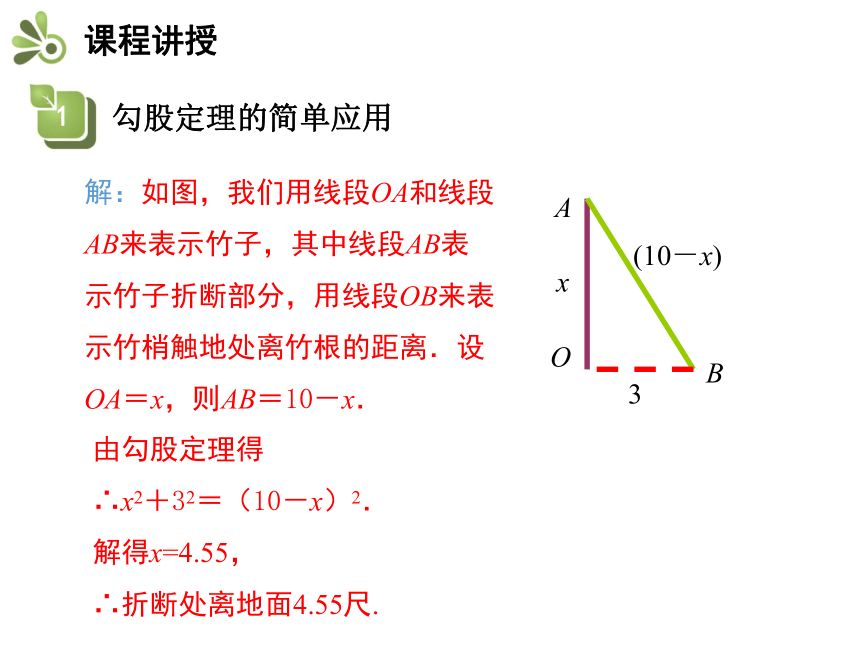
九章算术中的“折竹”问题:今有竹高一丈,
末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
课程讲授
1
勾股定理的简单应用
解:如图,我们用线段OA和线段
AB来表示竹子,其中线段AB表
示竹子折断部分,用线段OB来表
示竹梢触地处离竹根的距离.设
OA=x,则AB=10-x.
由勾股定理得
∴x2+32=(10-x)2.
解得x=4.55,
∴折断处离地面4.55尺.
A
O
B
x
(10-x)
3
课程讲授
1
勾股定理的简单应用
例2
如图,在△ABC中,AB=26,BC=20,BC边上的
中线AD=24,求AC.
解:∵AD是BC边上的中线,且BC=20,
D
C
B
A
∵AD2+BD2=576+100=676,
AB
2=262=676,
∴AD2+BD2=AB2,
∴
∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
课程讲授
1
勾股定理的简单应用
例3
如图,已知CD=6cm,AD=8cm,
∠ADC=90°,BC=24cm,AB=26cm,求阴影部分面积.
A
B
C
D
课程讲授
1
勾股定理的简单应用
A
B
C
D
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S阴影部分=S△ACB-S△ACD
=120-24
=96.
归纳:
1.勾股定理主要应用于求线段的长度、图形的周长、面积.
2.利用题中所给条件构造直角三角形,解决实际问题.
课程讲授
1
勾股定理的简单应用
随堂练习
1.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距(
)
A.25海里
B.30海里
C.40海里
D.50海里
C
随堂练习
2.如图,校园内有两棵树,一棵树高13
m,另一棵树高8
m,两树相距12
m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞(
)
A.10
m
B.11
m
C.12
m
D.13
m
D
随堂练习
3.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据不符合直角三角形的三边长的是(
)
A.3
cm,4
cm,5
cm
B.6
cm,8
cm,10
cm
C.5
cm,12
cm,13
cm
D.13
cm,16
cm,18
cm
D
随堂练习
4.如图,在△ABC中,AB=AC,D点在CB
延长线上,
求证:AD2-AB2=BD·CD.
A
B
C
D
E
证明:过点A作AE⊥BC于点E.
∵AB=AC,∴BE=CE.
在Rt
△ADE中,AD2=AE2+DE2.
在Rt
△ABE中,AB2=AE2+BE2.
=
DE2-
BE2
=
(DE+BE)·(
DE-
BE)
=
(DE+CE)·(
DE-
BE)
=BD·CD.
课堂小结
勾股定理的应用
勾股定理的简单应用
勾股定理的实际应用
3.3
勾股定理的简单应用
第3章
勾股定理
课程讲授
新知导入
随堂练习
课堂小结
知识要点
勾股定理的简单应用
新知导入
看一看:
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形。
新知导入
想一想:
已知桥面以上索塔AB的高,怎样计算AC,AD,AE,AF,AG的长.
A
B
C
E
F
G
D
课程讲授
1
勾股定理的简单应用
例1
九章算术中的“折竹”问题:今有竹高一丈,
末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
课程讲授
1
勾股定理的简单应用
解:如图,我们用线段OA和线段
AB来表示竹子,其中线段AB表
示竹子折断部分,用线段OB来表
示竹梢触地处离竹根的距离.设
OA=x,则AB=10-x.
由勾股定理得
∴x2+32=(10-x)2.
解得x=4.55,
∴折断处离地面4.55尺.
A
O
B
x
(10-x)
3
课程讲授
1
勾股定理的简单应用
例2
如图,在△ABC中,AB=26,BC=20,BC边上的
中线AD=24,求AC.
解:∵AD是BC边上的中线,且BC=20,
D
C
B
A
∵AD2+BD2=576+100=676,
AB
2=262=676,
∴AD2+BD2=AB2,
∴
∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
课程讲授
1
勾股定理的简单应用
例3
如图,已知CD=6cm,AD=8cm,
∠ADC=90°,BC=24cm,AB=26cm,求阴影部分面积.
A
B
C
D
课程讲授
1
勾股定理的简单应用
A
B
C
D
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S阴影部分=S△ACB-S△ACD
=120-24
=96.
归纳:
1.勾股定理主要应用于求线段的长度、图形的周长、面积.
2.利用题中所给条件构造直角三角形,解决实际问题.
课程讲授
1
勾股定理的简单应用
随堂练习
1.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距(
)
A.25海里
B.30海里
C.40海里
D.50海里
C
随堂练习
2.如图,校园内有两棵树,一棵树高13
m,另一棵树高8
m,两树相距12
m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞(
)
A.10
m
B.11
m
C.12
m
D.13
m
D
随堂练习
3.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据不符合直角三角形的三边长的是(
)
A.3
cm,4
cm,5
cm
B.6
cm,8
cm,10
cm
C.5
cm,12
cm,13
cm
D.13
cm,16
cm,18
cm
D
随堂练习
4.如图,在△ABC中,AB=AC,D点在CB
延长线上,
求证:AD2-AB2=BD·CD.
A
B
C
D
E
证明:过点A作AE⊥BC于点E.
∵AB=AC,∴BE=CE.
在Rt
△ADE中,AD2=AE2+DE2.
在Rt
△ABE中,AB2=AE2+BE2.
=
DE2-
BE2
=
(DE+BE)·(
DE-
BE)
=
(DE+CE)·(
DE-
BE)
=BD·CD.
课堂小结
勾股定理的应用
勾股定理的简单应用
勾股定理的实际应用
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
