鲁科版(2019)高中物理必修第二册导学案3.3离心现象
文档属性
| 名称 | 鲁科版(2019)高中物理必修第二册导学案3.3离心现象 |

|
|
| 格式 | docx | ||
| 文件大小 | 54.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览


文档简介
离心现象
【学习目标】
1.知道如果一个力或几个力的合力的效果是使物体产生向心加速度,它就是物体所受的向心力。会在具体问题中分析向心力的来源。
2.引导学生应用牛顿第二定律和有关向心力知识分析实例,使学生深刻理解向心力的基础知识。
3.熟练掌握应用向心力知识分析两类圆周运动模型的步骤和方法。
4.知道物体做离心运动的条件。
5.了解离心运动的应用和防止。
【学习重点】
1.理解做匀速圆周运动的物体受到的向心力是由某几个力的合力提供的,而不是一种特殊的力;找出向心力的来源,理解并掌握在匀速圆周运动中合外力提供向心力。
2.能用向心力公式解决有关圆周运动的实际问题。
3.物体做离心运动所满足的条件。对离心运动的理解及其实例分析。
【学习难点】
火车在倾斜弯道上转弯的圆周运动模型的建立;临界问题中临界条件的确定。
【学习过程】
一、车辆转弯时所需的向心力
1.汽车在水平路面转弯
(1)向心力来源:_____________________
(2)向心力方程:_____________________
(3)最大速度:_____________,受___________________的制约。
2.汽车、火车在内低外高的路面上转弯
(1)向心力来源:_____________________
(2)向心力方程:_____________________
(3)临界速度:_____________,受___________________的制约。
思考判断
(1)汽车在水平路面上正常转弯时所需要的向心力是滑动摩擦力提供的。( )
(2)铁路的轨道,内、外轨道都是一样高。( )
答案:(1)× (2)×
【例1】火车转弯可近似看成是做匀速圆周运动。当火车以规定速度行驶时,内外轨道均不受侧向挤压。现要降低火车转弯时的规定速度,须对铁路进行改造,从理论上讲以下措施可行的是( )
A.减小内外轨的高度差 B.增加内外轨的高度差
C.减小弯道半径 D.增大弯道半径
二、竖直平面内的圆周运动分析
1.汽车过拱桥
分类
分析
汽车过凸形桥
汽车过凹形桥
向心力
受力分析:
_____________________提供向心力
受力分析:
_____________________提供向心力
方程
压力
方程:
压力________重力,
当v=_________时N=0
方程:
压力_________重力
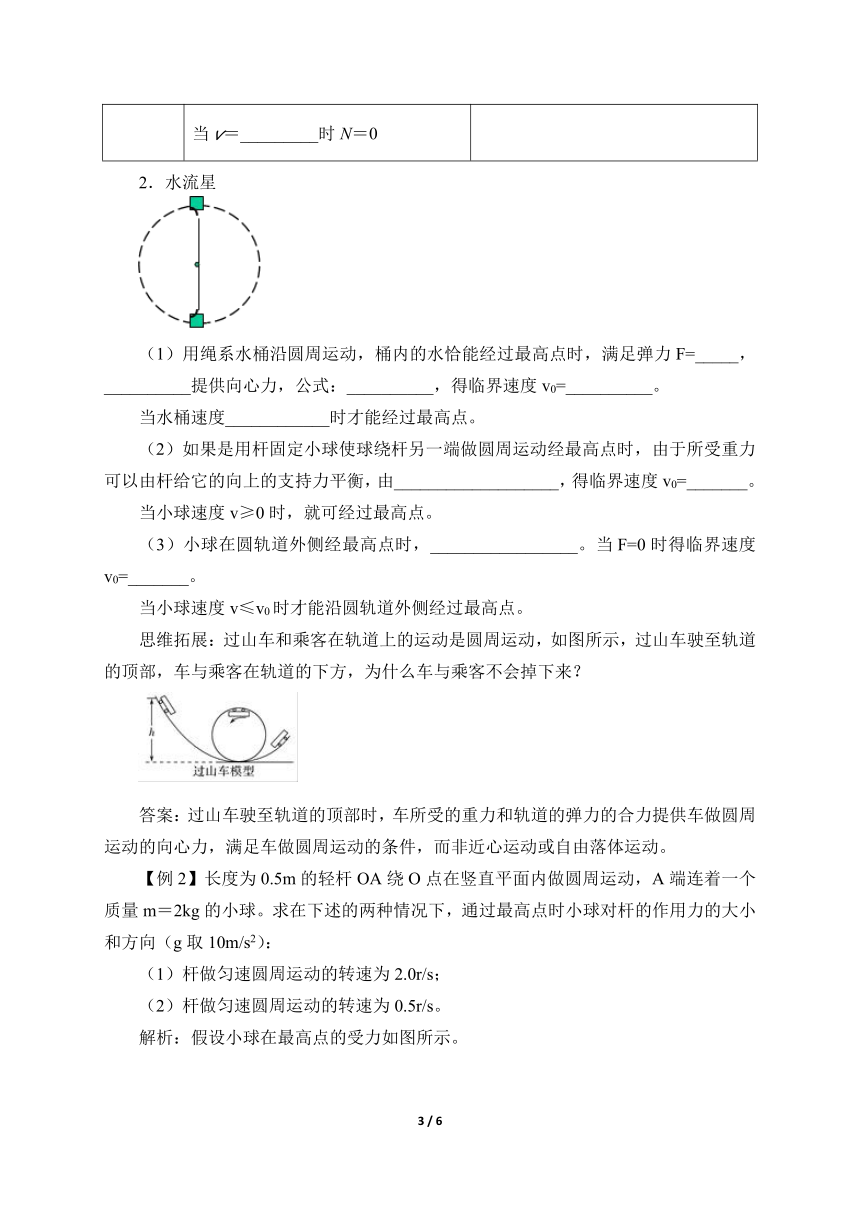
2.水流星
(1)用绳系水桶沿圆周运动,桶内的水恰能经过最高点时,满足弹力F=_____,__________提供向心力,公式:__________,得临界速度v0=__________。
当水桶速度____________时才能经过最高点。
(2)如果是用杆固定小球使球绕杆另一端做圆周运动经最高点时,由于所受重力可以由杆给它的向上的支持力平衡,由___________________,得临界速度v0=_______。
当小球速度v≥0时,就可经过最高点。
(3)小球在圆轨道外侧经最高点时,_________________。当F=0时得临界速度v0=_______。
当小球速度v≤v0时才能沿圆轨道外侧经过最高点。
思维拓展:过山车和乘客在轨道上的运动是圆周运动,如图所示,过山车驶至轨道的顶部,车与乘客在轨道的下方,为什么车与乘客不会掉下来?
答案:过山车驶至轨道的顶部时,车所受的重力和轨道的弹力的合力提供车做圆周运动的向心力,满足车做圆周运动的条件,而非近心运动或自由落体运动。
【例2】长度为0.5m的轻杆OA绕O点在竖直平面内做圆周运动,A端连着一个质量m=2kg的小球。求在下述的两种情况下,通过最高点时小球对杆的作用力的大小和方向(g取10m/s2):
(1)杆做匀速圆周运动的转速为2.0r/s;
(2)杆做匀速圆周运动的转速为0.5r/s。
解析:假设小球在最高点的受力如图所示。
(1)杆的转速为2.0r/s时,ω=2πn=4πrad/s
由牛顿第二定律得:F+mg=mLω2
故小球所受杆的作用力:
F=mLω2-mg=2×(0.5×42×π2-10)N≈138N
即:杆对小球提供了138N的拉力。
由牛顿第三定律知,小球对杆的拉力大小为138N,方向竖直向上。
(2)杆的转速为0.5r/s时,ω′=2πn′=πrad/s
同理可得小球所受杆的作用力
F=mLω′2-mg=2×(0.5×π2-10)N≈-10N。
力F为负值表示它的方向与受力分析中所假设的方向相反,故小球对杆的压力大小为10N,方向竖直向下。
三、生活中的离心运动
1.离心运动的概念:做匀速圆周运动的物体,在_________________或所受_____________不足以提供做圆周运动所需的向心力时,物体就做逐渐远离圆心的运动,称为离心运动。
2.要注意离心现象是做圆周运动的物体向心力不足,或失去向心力所致的现象,绝不可以错误地认为离心现象是离心力_________向心力的缘故。
3.物体做匀速圆周运动的条件:v0≠0;力的大小恒定且指向圆心,满足:F=mv2/r=mrω2=mr4π2/T2=mvω的供需关系。
当____________________________时,做离心运动;
当____________________________时,做近心运动;
当____________________________时,沿切线飞出。
4.离心运动的应用和防止
(1)离心运动的应用
①__________________________
②__________________________
③__________________________
④__________________________
(2)离心运动的防止
①车辆转弯时要________________
②转动的砂轮和飞轮要________________
【巩固练习】
1.在水平路面上稳定转弯的汽车,向心力是( )
A.水平面对汽车的静摩擦力
B.水平面对汽车的滑动摩擦力
C.汽车受到的重力和水平面对汽车的支持力的合力
D.汽车受到的重力、水平面对汽车的支持力和汽车的牵引力的合力
2.火车在水平轨道上转弯时,若转弯处内、外轨道一样高,则火车转弯时( )
A.对外轨产生向外的挤压作用
B.对内轨产生向外的挤压作用
C.对外轨产生向内的挤压作用
D.对内轨产生向内的挤压作用
3.已知质量为103kg的汽车,轮胎与地面间的最大静摩擦力为7000N,水平公路转弯处的半径为28m,g取10m/s2,则汽车转弯的最大速度为多少?
4.如图所示,光滑水平面上,小球m在拉力F作用下做匀速圆周运动。若小球运动到P点时,拉力F发生变化,关于小球运动情况的说法正确的是( )
4292600101600A.若拉力突然消失,小球将沿轨迹Pa做离心运动
B.若拉力突然变小,小球将沿轨迹Pa做离心运动
C.若拉力突然变大,小球将沿轨迹Pb做离心运动
D.若拉力突然变小,小球将沿轨迹Pc做离心运动
5.下列关于离心现象的说法正确的是( )
A.当物体所受的离心力大于向心力时产生离心现象
B.做匀速圆周运动的物体,当它所受的一切力都消失时,它将做背离圆心的圆周运动
C.做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将沿切线做直线运动
D.做匀速圆周运动的物体,当它所受的一切力都消失时,它将做曲线运动
41846504254506.如图所示,小球从“离心轨道”上滑下,若小球经过A点时开始脱离圆环,则小球将做( )
A.自由落体运动
B.平抛运动
C.斜上抛运动
D.竖直上抛运动
7.在人们经常见到的以下现象中,不属于离心现象的是( )
A.舞蹈演员在表演旋转动作时,裙子会张开
B.在雨中转动一下伞柄,伞面上的雨水会很快地沿伞面运动,到达边缘后雨水将沿切线方向飞出
C.满载黄砂或石子的卡车,在急转弯时,部分黄砂或石子会被甩出
D.守门员把足球踢出后,球在空中沿着弧线运动
8.下列哪些现象是为了防止物体产生离心现象的:①汽车转弯时要限制速度②转速很高的砂轮半径不能做得太大③在修筑铁路时,转弯处轨道的内轨要低于外轨④离心水泵工作时( )
A.①②③ B.②③④ C.①②④ D.①③④
9.物体做离心运动时,运动轨迹( )
A.一定是直线 B.一定是曲线
C.可能是直线,也可能是曲线 D.可能是圆
10.在注满水的玻璃管中放一个乒乓球,然后再用软木塞封住管口,将此玻璃管放在旋转的转盘上,且保持与盘相对静止,如图所示。则乒乓球会( )
4076700107950A.向外侧运动
B.向内侧运动
C.保持不动
D.条件不足,无法判断
11.如图所示,在水平固定的光滑平板上,有一质量为M的质点P,与穿过中央小孔H的轻绳一端连着。平板与小孔是光滑的,用手拉着绳子下端,使质点做半径为r的,角速度为ω的匀速圆周运动。若绳子迅速放松至某一长度R而拉紧,质点就能在以半径为R的圆周上做匀速圆周运动。求质点由半径r到R所需的时间。
【学习目标】
1.知道如果一个力或几个力的合力的效果是使物体产生向心加速度,它就是物体所受的向心力。会在具体问题中分析向心力的来源。
2.引导学生应用牛顿第二定律和有关向心力知识分析实例,使学生深刻理解向心力的基础知识。
3.熟练掌握应用向心力知识分析两类圆周运动模型的步骤和方法。
4.知道物体做离心运动的条件。
5.了解离心运动的应用和防止。
【学习重点】
1.理解做匀速圆周运动的物体受到的向心力是由某几个力的合力提供的,而不是一种特殊的力;找出向心力的来源,理解并掌握在匀速圆周运动中合外力提供向心力。
2.能用向心力公式解决有关圆周运动的实际问题。
3.物体做离心运动所满足的条件。对离心运动的理解及其实例分析。
【学习难点】
火车在倾斜弯道上转弯的圆周运动模型的建立;临界问题中临界条件的确定。
【学习过程】
一、车辆转弯时所需的向心力
1.汽车在水平路面转弯
(1)向心力来源:_____________________
(2)向心力方程:_____________________
(3)最大速度:_____________,受___________________的制约。
2.汽车、火车在内低外高的路面上转弯
(1)向心力来源:_____________________
(2)向心力方程:_____________________
(3)临界速度:_____________,受___________________的制约。
思考判断
(1)汽车在水平路面上正常转弯时所需要的向心力是滑动摩擦力提供的。( )
(2)铁路的轨道,内、外轨道都是一样高。( )
答案:(1)× (2)×
【例1】火车转弯可近似看成是做匀速圆周运动。当火车以规定速度行驶时,内外轨道均不受侧向挤压。现要降低火车转弯时的规定速度,须对铁路进行改造,从理论上讲以下措施可行的是( )
A.减小内外轨的高度差 B.增加内外轨的高度差
C.减小弯道半径 D.增大弯道半径
二、竖直平面内的圆周运动分析
1.汽车过拱桥
分类
分析
汽车过凸形桥
汽车过凹形桥
向心力
受力分析:
_____________________提供向心力
受力分析:
_____________________提供向心力
方程
压力
方程:
压力________重力,
当v=_________时N=0
方程:
压力_________重力
2.水流星
(1)用绳系水桶沿圆周运动,桶内的水恰能经过最高点时,满足弹力F=_____,__________提供向心力,公式:__________,得临界速度v0=__________。
当水桶速度____________时才能经过最高点。
(2)如果是用杆固定小球使球绕杆另一端做圆周运动经最高点时,由于所受重力可以由杆给它的向上的支持力平衡,由___________________,得临界速度v0=_______。
当小球速度v≥0时,就可经过最高点。
(3)小球在圆轨道外侧经最高点时,_________________。当F=0时得临界速度v0=_______。
当小球速度v≤v0时才能沿圆轨道外侧经过最高点。
思维拓展:过山车和乘客在轨道上的运动是圆周运动,如图所示,过山车驶至轨道的顶部,车与乘客在轨道的下方,为什么车与乘客不会掉下来?
答案:过山车驶至轨道的顶部时,车所受的重力和轨道的弹力的合力提供车做圆周运动的向心力,满足车做圆周运动的条件,而非近心运动或自由落体运动。
【例2】长度为0.5m的轻杆OA绕O点在竖直平面内做圆周运动,A端连着一个质量m=2kg的小球。求在下述的两种情况下,通过最高点时小球对杆的作用力的大小和方向(g取10m/s2):
(1)杆做匀速圆周运动的转速为2.0r/s;
(2)杆做匀速圆周运动的转速为0.5r/s。
解析:假设小球在最高点的受力如图所示。
(1)杆的转速为2.0r/s时,ω=2πn=4πrad/s
由牛顿第二定律得:F+mg=mLω2
故小球所受杆的作用力:
F=mLω2-mg=2×(0.5×42×π2-10)N≈138N
即:杆对小球提供了138N的拉力。
由牛顿第三定律知,小球对杆的拉力大小为138N,方向竖直向上。
(2)杆的转速为0.5r/s时,ω′=2πn′=πrad/s
同理可得小球所受杆的作用力
F=mLω′2-mg=2×(0.5×π2-10)N≈-10N。
力F为负值表示它的方向与受力分析中所假设的方向相反,故小球对杆的压力大小为10N,方向竖直向下。
三、生活中的离心运动
1.离心运动的概念:做匀速圆周运动的物体,在_________________或所受_____________不足以提供做圆周运动所需的向心力时,物体就做逐渐远离圆心的运动,称为离心运动。
2.要注意离心现象是做圆周运动的物体向心力不足,或失去向心力所致的现象,绝不可以错误地认为离心现象是离心力_________向心力的缘故。
3.物体做匀速圆周运动的条件:v0≠0;力的大小恒定且指向圆心,满足:F=mv2/r=mrω2=mr4π2/T2=mvω的供需关系。
当____________________________时,做离心运动;
当____________________________时,做近心运动;
当____________________________时,沿切线飞出。
4.离心运动的应用和防止
(1)离心运动的应用
①__________________________
②__________________________
③__________________________
④__________________________
(2)离心运动的防止
①车辆转弯时要________________
②转动的砂轮和飞轮要________________
【巩固练习】
1.在水平路面上稳定转弯的汽车,向心力是( )
A.水平面对汽车的静摩擦力
B.水平面对汽车的滑动摩擦力
C.汽车受到的重力和水平面对汽车的支持力的合力
D.汽车受到的重力、水平面对汽车的支持力和汽车的牵引力的合力
2.火车在水平轨道上转弯时,若转弯处内、外轨道一样高,则火车转弯时( )
A.对外轨产生向外的挤压作用
B.对内轨产生向外的挤压作用
C.对外轨产生向内的挤压作用
D.对内轨产生向内的挤压作用
3.已知质量为103kg的汽车,轮胎与地面间的最大静摩擦力为7000N,水平公路转弯处的半径为28m,g取10m/s2,则汽车转弯的最大速度为多少?
4.如图所示,光滑水平面上,小球m在拉力F作用下做匀速圆周运动。若小球运动到P点时,拉力F发生变化,关于小球运动情况的说法正确的是( )
4292600101600A.若拉力突然消失,小球将沿轨迹Pa做离心运动
B.若拉力突然变小,小球将沿轨迹Pa做离心运动
C.若拉力突然变大,小球将沿轨迹Pb做离心运动
D.若拉力突然变小,小球将沿轨迹Pc做离心运动
5.下列关于离心现象的说法正确的是( )
A.当物体所受的离心力大于向心力时产生离心现象
B.做匀速圆周运动的物体,当它所受的一切力都消失时,它将做背离圆心的圆周运动
C.做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将沿切线做直线运动
D.做匀速圆周运动的物体,当它所受的一切力都消失时,它将做曲线运动
41846504254506.如图所示,小球从“离心轨道”上滑下,若小球经过A点时开始脱离圆环,则小球将做( )
A.自由落体运动
B.平抛运动
C.斜上抛运动
D.竖直上抛运动
7.在人们经常见到的以下现象中,不属于离心现象的是( )
A.舞蹈演员在表演旋转动作时,裙子会张开
B.在雨中转动一下伞柄,伞面上的雨水会很快地沿伞面运动,到达边缘后雨水将沿切线方向飞出
C.满载黄砂或石子的卡车,在急转弯时,部分黄砂或石子会被甩出
D.守门员把足球踢出后,球在空中沿着弧线运动
8.下列哪些现象是为了防止物体产生离心现象的:①汽车转弯时要限制速度②转速很高的砂轮半径不能做得太大③在修筑铁路时,转弯处轨道的内轨要低于外轨④离心水泵工作时( )
A.①②③ B.②③④ C.①②④ D.①③④
9.物体做离心运动时,运动轨迹( )
A.一定是直线 B.一定是曲线
C.可能是直线,也可能是曲线 D.可能是圆
10.在注满水的玻璃管中放一个乒乓球,然后再用软木塞封住管口,将此玻璃管放在旋转的转盘上,且保持与盘相对静止,如图所示。则乒乓球会( )
4076700107950A.向外侧运动
B.向内侧运动
C.保持不动
D.条件不足,无法判断
11.如图所示,在水平固定的光滑平板上,有一质量为M的质点P,与穿过中央小孔H的轻绳一端连着。平板与小孔是光滑的,用手拉着绳子下端,使质点做半径为r的,角速度为ω的匀速圆周运动。若绳子迅速放松至某一长度R而拉紧,质点就能在以半径为R的圆周上做匀速圆周运动。求质点由半径r到R所需的时间。
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
