华师版八年级数学上册第14章勾股定理单元练习卷(word版,含答案)
文档属性
| 名称 | 华师版八年级数学上册第14章勾股定理单元练习卷(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 572.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-05 15:57:56 | ||
图片预览



文档简介
第14章达标测试卷
1.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.15
2.已知三组数据:①2、3、4;②3、4、5;③1、、2,分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的有( )
A.② B.①② C.①③ D.②③
3.用反证法证明“三角形的三个外角中至少有两个钝角”时,假设正确的是( )
A.假设三个外角都是锐角 B.假设三个外角中至少有一个钝角
C.假设三个外角都是钝角 D.假设三个外角中至多有一个钝角
4.如图,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在D′处,则重叠部分△AFC的面积是( )
A.8 B.10 C.20 D.32
(第4题) (第5题) (第6题)
5.如图,△ABC的顶点A、B、C在由边长为1的小正方形组成的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
6.如图,小明将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度为( )
A.12 m B.13 m C.16 m D.17 m
7.如图,长方体的长、宽、高分别为3 cm,1 cm,6 cm,如果一只小虫从点A开始爬行,经过两个侧面爬行到另一条侧棱的中点B处,那么这只小虫所爬行的最短路程为( )
A.5 cm B.4 cm C.6 cm D.7 cm
(第7题) (第8题)
8.如图,在长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长为( )
A. B. C. D.
9.在△ABC中,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是( )
A. B. C. D.
10.一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图,轮船从港口O沿北偏西20°的方向,行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M,N两点相距100海里,则∠NOF的度数为( )
(第10题)
A.50° B.60° C.70° D.80°
二、填空题(每题3分,共18分)
11.已知在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,∠C=90°,c=10,a∶b=3∶4,则a=.
12.一艘轮船以16海里/时的速度离开港口向东南方向航行,另一艘轮船在同时同地以12海里/时的速度向西南方向航行,则一个半小时后两船相距________海里.
13.如图,△ABC为等边三角形,BD为中线,延长BC至点E,使CE=CD=1,连结DE,则DE=_________.
14.如图,已知CA=CB,BD⊥AC于点D,BD=1,则数轴上点A所表示的数是________.
(第13题) (第14题) (第15题)
15.如图,△ABC≌△FED,∠C=∠EDF=90°,点E在AB边上,点C、D、B、F在同一条直线上,AC=3,AB=4,则DE的长为________.
16.在△ABC中,AB=,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连结CD,则线段CD的长为__________.
三、解答题(17,19题每题8分,18,20,21,22题每题9分,共52分)
17.如图,△ABC是直角三角形,∠ACB=90°,BC=12,以AC为边向外作正方形,其面积为25,以AB为边向外作长方形,长方形的宽AE=5,求长方形ABDE的面积.
(第17题)
18.如图,在长方形ABCD中,AB=24,AD=50,E是AD上一点,且AE∶ED=9∶16.
(1)求BE、CE的长.
(2)△BEC是直角三角形吗?为什么?
(第18题)
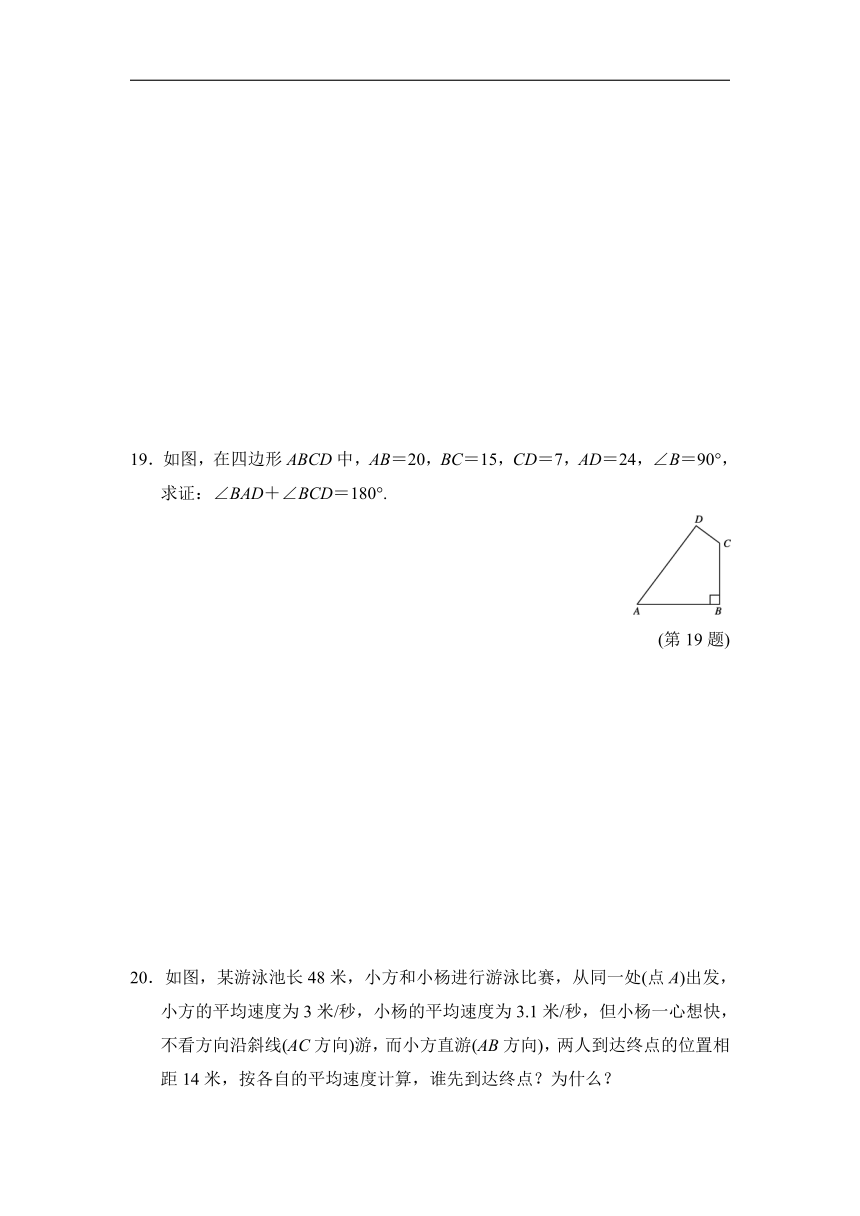
19.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠BAD+∠BCD=180°.
(第19题)
20.如图,某游泳池长48米,小方和小杨进行游泳比赛,从同一处(点A)出发,小方的平均速度为3米/秒,小杨的平均速度为3.1米/秒,但小杨一心想快,不看方向沿斜线(AC方向)游,而小方直游(AB方向),两人到达终点的位置相距14米,按各自的平均速度计算,谁先到达终点?为什么?
(第20题)
21.如图,这是一个供滑板爱好者使用的U型池,该U型池可以看成是由一个长方体去掉一个“半圆柱”而形成的,中间可供滑行部分的截面是半径为2 m的半圆,其边缘AB=CD=10 m,点E在CD上,且CE=2 m,若一滑板爱好者从点A滑到点E,则他滑行的最短距离是多少?(边缘部分的厚度忽略不计,π取整数3)
(第21题)
22.如图,A、B两村在河的同侧,且AB= km,A、B两村到河的距离分别为AC=1 km,BD=3 km.现要在河边CD上建一水厂分别向A、B两村输送自来水,铺设水管的工程费每千米需3 000元.请你在河边CD上选择水厂的位置O,使铺设水管的费用最省,并求出铺设水管的总费用.
(第22题)
答案
一、1.A 2.D 3.D 4.B 5.C 6.D 7.A
8.B 点拨:由折叠的性质可知AB=AE=DC,∠E=∠B=∠D=90°,BC=EC=6.在△AEF和△CDF中,∵∠E=∠D,∠EFA=∠DFC,AE=CD,∴△AEF≌△CDF(A.A.S.),∴EF=DF. 设DF=x,则EF=x,∴FC=EC-EF=6-x.
在Rt△CDF中,由勾股定理可知FC2=DF2+CD2,∴(6-x)2=x2+42,解得x=,故选B.
9.A
10.C 点拨:由题意知OM=60海里,ON=80海里,MN=100海里,∴OM2+ON2=MN2,∴∠MON=90°.∵∠EOM=20°,∴∠NOF=180°-20°-90°=70°.
二、11.6 12.30 13.
14.1- 点拨:在Rt△BDC中,∵BD=1,CD=2,∴CB===.∴CA=CB=,∴数轴上点A所表示的数是1-.
15.
16.或 点拨:①如图①,当点D与点C在AB同侧时,BD=AB=,延长BC交AD于点E,∵∠ABC=45°,△ABD为等腰直角三角形,∴∠ABC=∠DBC=45°,
∴BE⊥AD,AE=DE=AD==×=2,
∴BE==
=2.又∵BC=1,∴CE=1,∴CD===;②如图②,当点D与点C在AB异侧时,作DE⊥CB,交CB的延长线于点E,
易知DE=BE=2.又∵BC=1,
∴EC=3,∴CD===.
(第16题)
三、17.解:∵以AC为边向外作正方形,其面积为25,∴AC2=25.
在Rt△ACB中,∵BC=12,AC2=25,
∴由勾股定理可知AB====13.
∵AE=5,∴S长方形ABDE=AB×AE=13×5=65.
18.解:(1)∵AE∶ED=9∶16,AD=50,
∴AE=×50=18,ED=×50=32.
∵四边形ABCD为长方形,
∴∠A=∠D=90°,CD=AB=24.
∴BE===30,
CE===40.
(2)△BEC是直角三角形.
理由如下:
∵BE2+CE2=302+402=2 500,BC2=502=2 500,∴BE2+CE2=BC2.
∴△BEC是直角三角形.
19.证明:连结AC,在Rt△ABC中,AC2=AB2+BC2=202+152=625.在△ACD中,∵CD2+AD2=72+242=625=AC2,∴△ACD是直角三角形,且∠D=90°.∵四边形ABCD的内角和为360°,且∠B=90°,∠D=90°,∴∠BAD+∠BCD=180°.
20.解:小方先到达终点.理由如下:由题意可知AB=48米,BC=14米,
∴小方用时48÷3=16(秒),在Rt△ABC中,∵AC===50(米),
∴小杨用时50÷3.1=16(秒).∵16<16,∴小方用时少,即小方先到达终点.
21.解:如图,作出U型池的侧面展开图,连结AE,则AE为所求的最短距离.
(第21题)
由题意可知,AD=≈6(m),DE=DC-CE=8 m,在Rt△ADE中,
∵∠D=90°,∴由勾股定理,得AD2+DE2=AE2,∴AE=≈=10 (m).
答:他滑行的最短距离约是10 m.
22.解:如图所示,作点A关于CD的对称点A′,连结BA′交CD于点O,连结AO,则点O即为水厂的位置.过点A′作A′E∥CD交BD的延长线于点E,过点A作AF⊥BD于点F,∴BF=BD-FD=BD-AC=3-1=2(km).
在Rt△ABF中,∵AF2+BF2=AB2,∴AF2=13-22=9,即AF=3 km.
∴A′E=AF=3 km.
在Rt△A′BE中,BE=BD+DE=BD+A′C=BD+AC=3+1=4(km),
A′B2=A′E2+BE2,
即A′B2=32+42=52,∴A′B=5 km.
又易知OA+OB=OA′+OB=A′B,
∴3 000×5=15 000(元),故铺设水管的总费用为15 000元.
(第22题)
1.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.15
2.已知三组数据:①2、3、4;②3、4、5;③1、、2,分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的有( )
A.② B.①② C.①③ D.②③
3.用反证法证明“三角形的三个外角中至少有两个钝角”时,假设正确的是( )
A.假设三个外角都是锐角 B.假设三个外角中至少有一个钝角
C.假设三个外角都是钝角 D.假设三个外角中至多有一个钝角
4.如图,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在D′处,则重叠部分△AFC的面积是( )
A.8 B.10 C.20 D.32
(第4题) (第5题) (第6题)
5.如图,△ABC的顶点A、B、C在由边长为1的小正方形组成的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
6.如图,小明将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度为( )
A.12 m B.13 m C.16 m D.17 m
7.如图,长方体的长、宽、高分别为3 cm,1 cm,6 cm,如果一只小虫从点A开始爬行,经过两个侧面爬行到另一条侧棱的中点B处,那么这只小虫所爬行的最短路程为( )
A.5 cm B.4 cm C.6 cm D.7 cm
(第7题) (第8题)
8.如图,在长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长为( )
A. B. C. D.
9.在△ABC中,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是( )
A. B. C. D.
10.一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图,轮船从港口O沿北偏西20°的方向,行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M,N两点相距100海里,则∠NOF的度数为( )
(第10题)
A.50° B.60° C.70° D.80°
二、填空题(每题3分,共18分)
11.已知在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,∠C=90°,c=10,a∶b=3∶4,则a=.
12.一艘轮船以16海里/时的速度离开港口向东南方向航行,另一艘轮船在同时同地以12海里/时的速度向西南方向航行,则一个半小时后两船相距________海里.
13.如图,△ABC为等边三角形,BD为中线,延长BC至点E,使CE=CD=1,连结DE,则DE=_________.
14.如图,已知CA=CB,BD⊥AC于点D,BD=1,则数轴上点A所表示的数是________.
(第13题) (第14题) (第15题)
15.如图,△ABC≌△FED,∠C=∠EDF=90°,点E在AB边上,点C、D、B、F在同一条直线上,AC=3,AB=4,则DE的长为________.
16.在△ABC中,AB=,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连结CD,则线段CD的长为__________.
三、解答题(17,19题每题8分,18,20,21,22题每题9分,共52分)
17.如图,△ABC是直角三角形,∠ACB=90°,BC=12,以AC为边向外作正方形,其面积为25,以AB为边向外作长方形,长方形的宽AE=5,求长方形ABDE的面积.
(第17题)
18.如图,在长方形ABCD中,AB=24,AD=50,E是AD上一点,且AE∶ED=9∶16.
(1)求BE、CE的长.
(2)△BEC是直角三角形吗?为什么?
(第18题)
19.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠BAD+∠BCD=180°.
(第19题)
20.如图,某游泳池长48米,小方和小杨进行游泳比赛,从同一处(点A)出发,小方的平均速度为3米/秒,小杨的平均速度为3.1米/秒,但小杨一心想快,不看方向沿斜线(AC方向)游,而小方直游(AB方向),两人到达终点的位置相距14米,按各自的平均速度计算,谁先到达终点?为什么?
(第20题)
21.如图,这是一个供滑板爱好者使用的U型池,该U型池可以看成是由一个长方体去掉一个“半圆柱”而形成的,中间可供滑行部分的截面是半径为2 m的半圆,其边缘AB=CD=10 m,点E在CD上,且CE=2 m,若一滑板爱好者从点A滑到点E,则他滑行的最短距离是多少?(边缘部分的厚度忽略不计,π取整数3)
(第21题)
22.如图,A、B两村在河的同侧,且AB= km,A、B两村到河的距离分别为AC=1 km,BD=3 km.现要在河边CD上建一水厂分别向A、B两村输送自来水,铺设水管的工程费每千米需3 000元.请你在河边CD上选择水厂的位置O,使铺设水管的费用最省,并求出铺设水管的总费用.
(第22题)
答案
一、1.A 2.D 3.D 4.B 5.C 6.D 7.A
8.B 点拨:由折叠的性质可知AB=AE=DC,∠E=∠B=∠D=90°,BC=EC=6.在△AEF和△CDF中,∵∠E=∠D,∠EFA=∠DFC,AE=CD,∴△AEF≌△CDF(A.A.S.),∴EF=DF. 设DF=x,则EF=x,∴FC=EC-EF=6-x.
在Rt△CDF中,由勾股定理可知FC2=DF2+CD2,∴(6-x)2=x2+42,解得x=,故选B.
9.A
10.C 点拨:由题意知OM=60海里,ON=80海里,MN=100海里,∴OM2+ON2=MN2,∴∠MON=90°.∵∠EOM=20°,∴∠NOF=180°-20°-90°=70°.
二、11.6 12.30 13.
14.1- 点拨:在Rt△BDC中,∵BD=1,CD=2,∴CB===.∴CA=CB=,∴数轴上点A所表示的数是1-.
15.
16.或 点拨:①如图①,当点D与点C在AB同侧时,BD=AB=,延长BC交AD于点E,∵∠ABC=45°,△ABD为等腰直角三角形,∴∠ABC=∠DBC=45°,
∴BE⊥AD,AE=DE=AD==×=2,
∴BE==
=2.又∵BC=1,∴CE=1,∴CD===;②如图②,当点D与点C在AB异侧时,作DE⊥CB,交CB的延长线于点E,
易知DE=BE=2.又∵BC=1,
∴EC=3,∴CD===.
(第16题)
三、17.解:∵以AC为边向外作正方形,其面积为25,∴AC2=25.
在Rt△ACB中,∵BC=12,AC2=25,
∴由勾股定理可知AB====13.
∵AE=5,∴S长方形ABDE=AB×AE=13×5=65.
18.解:(1)∵AE∶ED=9∶16,AD=50,
∴AE=×50=18,ED=×50=32.
∵四边形ABCD为长方形,
∴∠A=∠D=90°,CD=AB=24.
∴BE===30,
CE===40.
(2)△BEC是直角三角形.
理由如下:
∵BE2+CE2=302+402=2 500,BC2=502=2 500,∴BE2+CE2=BC2.
∴△BEC是直角三角形.
19.证明:连结AC,在Rt△ABC中,AC2=AB2+BC2=202+152=625.在△ACD中,∵CD2+AD2=72+242=625=AC2,∴△ACD是直角三角形,且∠D=90°.∵四边形ABCD的内角和为360°,且∠B=90°,∠D=90°,∴∠BAD+∠BCD=180°.
20.解:小方先到达终点.理由如下:由题意可知AB=48米,BC=14米,
∴小方用时48÷3=16(秒),在Rt△ABC中,∵AC===50(米),
∴小杨用时50÷3.1=16(秒).∵16<16,∴小方用时少,即小方先到达终点.
21.解:如图,作出U型池的侧面展开图,连结AE,则AE为所求的最短距离.
(第21题)
由题意可知,AD=≈6(m),DE=DC-CE=8 m,在Rt△ADE中,
∵∠D=90°,∴由勾股定理,得AD2+DE2=AE2,∴AE=≈=10 (m).
答:他滑行的最短距离约是10 m.
22.解:如图所示,作点A关于CD的对称点A′,连结BA′交CD于点O,连结AO,则点O即为水厂的位置.过点A′作A′E∥CD交BD的延长线于点E,过点A作AF⊥BD于点F,∴BF=BD-FD=BD-AC=3-1=2(km).
在Rt△ABF中,∵AF2+BF2=AB2,∴AF2=13-22=9,即AF=3 km.
∴A′E=AF=3 km.
在Rt△A′BE中,BE=BD+DE=BD+A′C=BD+AC=3+1=4(km),
A′B2=A′E2+BE2,
即A′B2=32+42=52,∴A′B=5 km.
又易知OA+OB=OA′+OB=A′B,
∴3 000×5=15 000(元),故铺设水管的总费用为15 000元.
(第22题)
