人教B版(2019)高中数学选择性必修第一册 2.2.2 第1课时 直线的点斜式方程与斜截式方程(共23张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 2.2.2 第1课时 直线的点斜式方程与斜截式方程(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 738.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 14:16:37 | ||
图片预览






文档简介
第1课时 直线的点斜式方程与斜截式方程
核心素养
1.理解直线与方程的关系.(数学抽象)
2.理解点斜式方程和斜截式方程的推导,并能明确其适用条件.(逻辑推理)
3.知道直线的点斜式和斜截式方程的内在联系和参数含义.(逻辑推理、直观想象)
4.能利用直线的点斜式方程和斜截式方程解决一些相关实际问题.(数学运算)
思维脉络
激趣诱思
知识点拨
问题1 一次函数y=kx+b的图像是一条直线l1,如果把x,y看做未知数,那么y=kx+b就是一个方程.那么直线l1上的点的坐标和方程的解之间有什么关系呢?
问题2 在平面直角坐标系内,如果一条直线l经过的一个定点P0(x0,y0),其斜率为k,能否将直线上所有的点的坐标(x,y)满足的关系表示出来呢?
结论展示问题1 提示(1)直线l1上的点的坐标都是二元方程y=kx+b的解.
(2)以方程y=kx+b的解为坐标的点都在直线l1上.
激趣诱思
知识点拨
1.直线与方程
一般地,如果直线l上点的坐标都是方程F(x,y)=0的解,而且以方程F(x,y)=0的解为坐标的点都在直线l上,则称F(x,y)=0为直线l的方程,而直线l称为方程F(x,y)=0的直线.此时,为了简单起见,“直线l”也可说成“直线F(x,y)=0”,并且记作l:F(x,y)=0.
微判断
(1)如图所示,线段AB的方程为y=x+1.( )
(2)在平面直角坐标系中,y轴所在直线方程为y=0.( )
答案:(1)× (2)×
激趣诱思
知识点拨
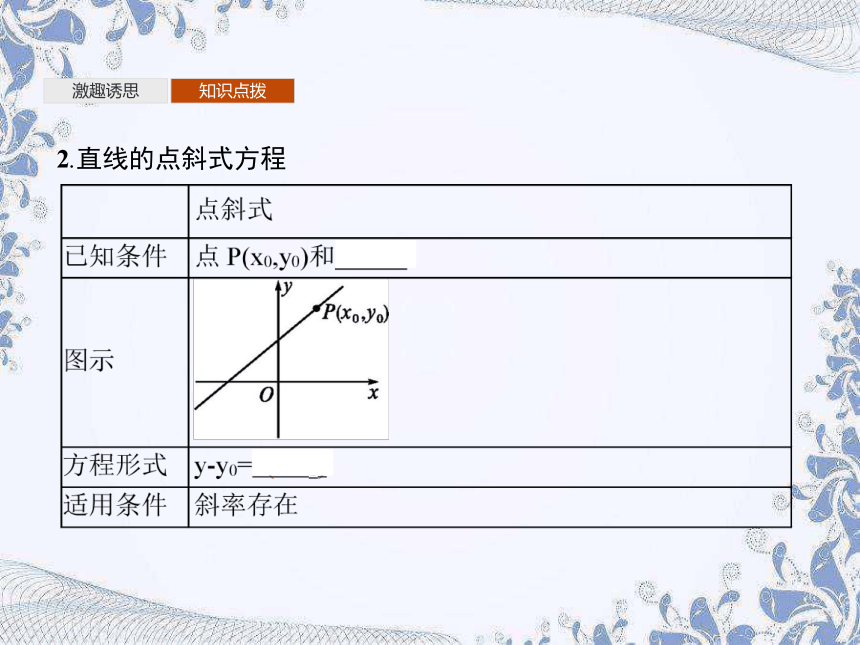
2.直线的点斜式方程
激趣诱思
知识点拨
微判断
直线y-3=m(x+9)恒过定点(9,-3).( )
答案:×
微练习
过点(1,1)且倾斜角为45°的直线的点斜式方程为 .?
答案:y-1=x-1
微思考
激趣诱思
知识点拨
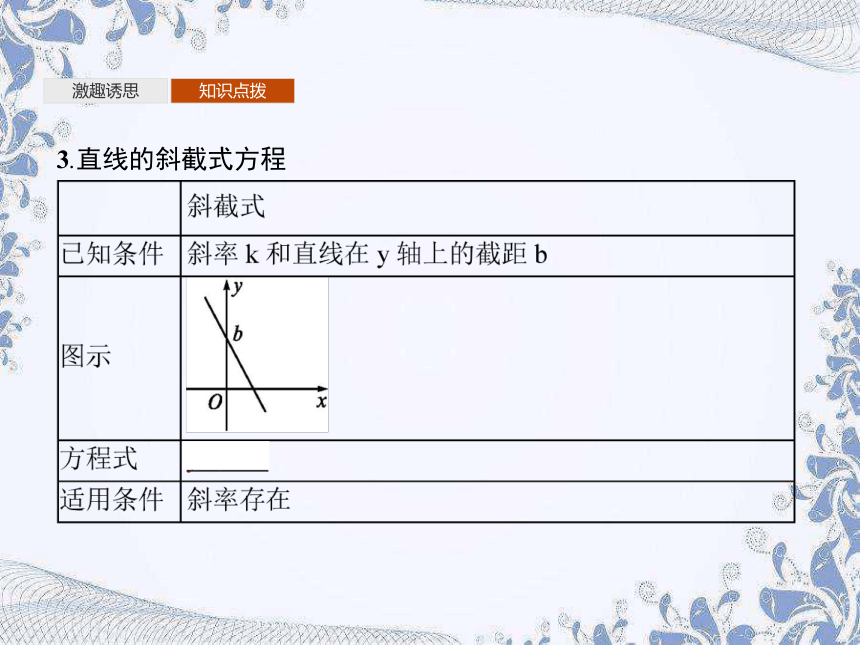
3.直线的斜截式方程
激趣诱思
知识点拨
名师点析 (1)用斜截式求直线方程,只要确定直线的斜率和截距即可,同时要特别注意截距和距离的区别.
(2)直线的斜截式方程y=kx+b不仅形式简单,而且特点明显,k是直线的斜率,b是直线在y轴上的截距,只要确定了k和b的值,直线的图像就一目了然.因此,在解决直线的图像问题时,常通过把直线方程化为斜截式方程,利用k,b的几何意义进行判断.
激趣诱思
知识点拨
微判断
(1)直线在y轴上的截距是直线与y轴交点到原点的距离. ( )
(2)直线y=kx-b在y轴上的截距为b. ( )
答案:(1)× (2)×
激趣诱思
知识点拨
微练习
(1)已知直线的斜率是2,且在y轴上的截距是-3,则此直线的方程是( )
A.y=2x-3 B.y=2x+3
C.y=-2x-3 D.y=-2x+3
答案:A
(2)直线y=kx+b通过第一、三、四象限,则有( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
答案:B
探究一
探究二
当堂检测
直线的点斜式方程
例1求满足下列条件的直线的方程:
(1)过点P(-4,3),斜率k=-2;
(2)过点P(2,-5),且与x轴平行;
(3)过点P(3,-1),且与y轴平行.
分析利用直线的点斜式方程及特殊位置的直线表示形式解答.
解:(1)直线过点P(-4,3),斜率k=-2,由点斜式得y-3=-2(x+4),整理得所求方程为2x+y+5=0.
(2)直线过点P(2,-5),且与x轴平行,则斜率k=0,
故所求直线方程为y+5=0(x-2),即y=-5.
(3)直线与y轴平行,说明斜率不存在,
又因为直线过点P(3,-1),所以直线的方程为x=3.
探究一
探究二
当堂检测
反思感悟 利用点斜式求直线方程的步骤
(1)确定直线要经过的定点(x0,y0);
(2)明确直线的斜率k;
(3)由点斜式直接写出直线方程.
注意:点斜式使用的前提条件是斜率存在,当斜率不存在时,直线没有点斜式方程,其方程为x=x0.
探究一
探究二
当堂检测
变式训练求斜率是直线x-y+1=0的斜率的3倍,且分别满足下列条件的直线方程.
(1)经过点P(3,4);
(2)在x轴上的截距是-5.
解:由x-y+1=0,得y=x+1,
∴直线x-y+1=0的斜率为1.
由题意可得,所求直线的斜率k=3.
(1)所求直线的方程是y-4=3(x-3),即3x-y-5=0.
(2)由题意知直线经过点(-5,0),所求直线的方程是y-0=3(x+5),即3x-y+15=0.
探究一
探究二
当堂检测
直线的斜截式方程
例2已知直线l的斜率为2,在y轴上的截距为m.
(1)求直线l的方程;
(2)当m为何值时,直线通过(1,1)点?
分析(1)直接套用直线的斜截式方程;(2)将点(1,1)代入所设方程求m.
解:(1)利用直线的斜截式方程,可得方程为y=2x+m.
(2)只需将点(1,1)代入直线y=2x+m,有1=2×1+m,所以m=-1.
探究一
探究二
当堂检测
反思感悟 对直线的斜截式方程的理解要注意以下几点:
(1)由直线的斜截式方程的推导过程可以看出,在点斜式中若点P(x0,y0)为直线l与y轴的交点,得到的直线方程即为斜截式,因此斜截式为点斜式的特殊情况.
(2)直线与x轴垂直时,斜率不存在,不能用直线方程的斜截式表示.因此,斜截式方程不能表示与x轴垂直的直线.
(3)斜截式方程y=kx+b的特点:左端y的系数恒为1,右端x的系数k和常数项b均有明显的几何意义,k是直线的斜率,b是直线在y轴上的截距,截距实质上为直线与y轴交点的纵坐标,直线与y轴的交点与原点的距离为|b|.
探究一
探究二
当堂检测
延伸探究 (1)将本例的条件“在y轴上的截距为m”改为“在x轴上的截距为m”,如何求直线的方程?
(2)将本例的条件不变,试问m为何值时,直线与坐标轴所围成的三角形的面积为1?
解:(1)直线在x轴上的截距为m,即直线过点(m,0),又已知直线的斜率为2,则由直线的点斜式方程,可得所求直线方程为y-0=2(x-m),即y=2x-2m.
探究一
探究二
当堂检测
1.已知直线的方程是y+2=-x-1,则( )
A.直线经过点(-1,2),斜率为-1
B.直线经过点(2,-1),斜率为-1
C.直线经过点(-1,-2),斜率为-1
D.直线经过点(-2,-1),斜率为1
解析:由y+2=-x-1,得y+2=-(x+1),所以直线的斜率为-1,过点(-1,-2).
答案:C
探究一
探究二
当堂检测
答案:B
探究一
探究二
当堂检测
3.已知直线的倾斜角为60°,在y轴上的截距为-2,则此直线的方程为( )
答案:D
探究一
探究二
当堂检测
4.与直线y=2x+1垂直,且在y轴上的截距为4的直线的斜截式方程为( )
答案:D
探究一
探究二
当堂检测
5.已知直线l过点P(2,1),且直线l的斜率为直线x-4y+3=0的斜率的2倍,则直线l的点斜式方程为 .?
探究一
探究二
当堂检测
6.已知直线l的斜率与直线3x-2y=6的斜率相等,且直线l在x轴上的截距比在y轴上的截距大1,求直线l的斜截式方程.
核心素养
1.理解直线与方程的关系.(数学抽象)
2.理解点斜式方程和斜截式方程的推导,并能明确其适用条件.(逻辑推理)
3.知道直线的点斜式和斜截式方程的内在联系和参数含义.(逻辑推理、直观想象)
4.能利用直线的点斜式方程和斜截式方程解决一些相关实际问题.(数学运算)
思维脉络
激趣诱思
知识点拨
问题1 一次函数y=kx+b的图像是一条直线l1,如果把x,y看做未知数,那么y=kx+b就是一个方程.那么直线l1上的点的坐标和方程的解之间有什么关系呢?
问题2 在平面直角坐标系内,如果一条直线l经过的一个定点P0(x0,y0),其斜率为k,能否将直线上所有的点的坐标(x,y)满足的关系表示出来呢?
结论展示问题1 提示(1)直线l1上的点的坐标都是二元方程y=kx+b的解.
(2)以方程y=kx+b的解为坐标的点都在直线l1上.
激趣诱思
知识点拨
1.直线与方程
一般地,如果直线l上点的坐标都是方程F(x,y)=0的解,而且以方程F(x,y)=0的解为坐标的点都在直线l上,则称F(x,y)=0为直线l的方程,而直线l称为方程F(x,y)=0的直线.此时,为了简单起见,“直线l”也可说成“直线F(x,y)=0”,并且记作l:F(x,y)=0.
微判断
(1)如图所示,线段AB的方程为y=x+1.( )
(2)在平面直角坐标系中,y轴所在直线方程为y=0.( )
答案:(1)× (2)×
激趣诱思
知识点拨
2.直线的点斜式方程
激趣诱思
知识点拨
微判断
直线y-3=m(x+9)恒过定点(9,-3).( )
答案:×
微练习
过点(1,1)且倾斜角为45°的直线的点斜式方程为 .?
答案:y-1=x-1
微思考
激趣诱思
知识点拨
3.直线的斜截式方程
激趣诱思
知识点拨
名师点析 (1)用斜截式求直线方程,只要确定直线的斜率和截距即可,同时要特别注意截距和距离的区别.
(2)直线的斜截式方程y=kx+b不仅形式简单,而且特点明显,k是直线的斜率,b是直线在y轴上的截距,只要确定了k和b的值,直线的图像就一目了然.因此,在解决直线的图像问题时,常通过把直线方程化为斜截式方程,利用k,b的几何意义进行判断.
激趣诱思
知识点拨
微判断
(1)直线在y轴上的截距是直线与y轴交点到原点的距离. ( )
(2)直线y=kx-b在y轴上的截距为b. ( )
答案:(1)× (2)×
激趣诱思
知识点拨
微练习
(1)已知直线的斜率是2,且在y轴上的截距是-3,则此直线的方程是( )
A.y=2x-3 B.y=2x+3
C.y=-2x-3 D.y=-2x+3
答案:A
(2)直线y=kx+b通过第一、三、四象限,则有( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
答案:B
探究一
探究二
当堂检测
直线的点斜式方程
例1求满足下列条件的直线的方程:
(1)过点P(-4,3),斜率k=-2;
(2)过点P(2,-5),且与x轴平行;
(3)过点P(3,-1),且与y轴平行.
分析利用直线的点斜式方程及特殊位置的直线表示形式解答.
解:(1)直线过点P(-4,3),斜率k=-2,由点斜式得y-3=-2(x+4),整理得所求方程为2x+y+5=0.
(2)直线过点P(2,-5),且与x轴平行,则斜率k=0,
故所求直线方程为y+5=0(x-2),即y=-5.
(3)直线与y轴平行,说明斜率不存在,
又因为直线过点P(3,-1),所以直线的方程为x=3.
探究一
探究二
当堂检测
反思感悟 利用点斜式求直线方程的步骤
(1)确定直线要经过的定点(x0,y0);
(2)明确直线的斜率k;
(3)由点斜式直接写出直线方程.
注意:点斜式使用的前提条件是斜率存在,当斜率不存在时,直线没有点斜式方程,其方程为x=x0.
探究一
探究二
当堂检测
变式训练求斜率是直线x-y+1=0的斜率的3倍,且分别满足下列条件的直线方程.
(1)经过点P(3,4);
(2)在x轴上的截距是-5.
解:由x-y+1=0,得y=x+1,
∴直线x-y+1=0的斜率为1.
由题意可得,所求直线的斜率k=3.
(1)所求直线的方程是y-4=3(x-3),即3x-y-5=0.
(2)由题意知直线经过点(-5,0),所求直线的方程是y-0=3(x+5),即3x-y+15=0.
探究一
探究二
当堂检测
直线的斜截式方程
例2已知直线l的斜率为2,在y轴上的截距为m.
(1)求直线l的方程;
(2)当m为何值时,直线通过(1,1)点?
分析(1)直接套用直线的斜截式方程;(2)将点(1,1)代入所设方程求m.
解:(1)利用直线的斜截式方程,可得方程为y=2x+m.
(2)只需将点(1,1)代入直线y=2x+m,有1=2×1+m,所以m=-1.
探究一
探究二
当堂检测
反思感悟 对直线的斜截式方程的理解要注意以下几点:
(1)由直线的斜截式方程的推导过程可以看出,在点斜式中若点P(x0,y0)为直线l与y轴的交点,得到的直线方程即为斜截式,因此斜截式为点斜式的特殊情况.
(2)直线与x轴垂直时,斜率不存在,不能用直线方程的斜截式表示.因此,斜截式方程不能表示与x轴垂直的直线.
(3)斜截式方程y=kx+b的特点:左端y的系数恒为1,右端x的系数k和常数项b均有明显的几何意义,k是直线的斜率,b是直线在y轴上的截距,截距实质上为直线与y轴交点的纵坐标,直线与y轴的交点与原点的距离为|b|.
探究一
探究二
当堂检测
延伸探究 (1)将本例的条件“在y轴上的截距为m”改为“在x轴上的截距为m”,如何求直线的方程?
(2)将本例的条件不变,试问m为何值时,直线与坐标轴所围成的三角形的面积为1?
解:(1)直线在x轴上的截距为m,即直线过点(m,0),又已知直线的斜率为2,则由直线的点斜式方程,可得所求直线方程为y-0=2(x-m),即y=2x-2m.
探究一
探究二
当堂检测
1.已知直线的方程是y+2=-x-1,则( )
A.直线经过点(-1,2),斜率为-1
B.直线经过点(2,-1),斜率为-1
C.直线经过点(-1,-2),斜率为-1
D.直线经过点(-2,-1),斜率为1
解析:由y+2=-x-1,得y+2=-(x+1),所以直线的斜率为-1,过点(-1,-2).
答案:C
探究一
探究二
当堂检测
答案:B
探究一
探究二
当堂检测
3.已知直线的倾斜角为60°,在y轴上的截距为-2,则此直线的方程为( )
答案:D
探究一
探究二
当堂检测
4.与直线y=2x+1垂直,且在y轴上的截距为4的直线的斜截式方程为( )
答案:D
探究一
探究二
当堂检测
5.已知直线l过点P(2,1),且直线l的斜率为直线x-4y+3=0的斜率的2倍,则直线l的点斜式方程为 .?
探究一
探究二
当堂检测
6.已知直线l的斜率与直线3x-2y=6的斜率相等,且直线l在x轴上的截距比在y轴上的截距大1,求直线l的斜截式方程.
